4.1.1 梯度—输送理论
4.1.1.1 基本原理
恶臭扩散的梯度—输送理论是在湍流半经验理论的基础上发展起来的。在描写湍流运动的湍流平均运动方程中,出现了由湍流脉动速度所产生的附加项——雷诺应力项。它们表示单位时间内通过单位面积的动量,即湍流所引起的摩擦力,又称为湍流黏性应力。正是这些湍流黏性应力体现了脉动速度对包括平均运动在内的整个流场的影响。此外,它们还是湍流流场最重要的性质——湍流强度和湍流输送速率的量度[43-44]。
湍流半经验理论的核心思想是试图在雷诺应力与平均速度分布之间引入某些经验关系,以此说明脉动速度与平均运动的相互作用及流场的各种性质。其基本假定来自分子过程的比拟,假设湍流所引起的动量通量与局部的平均速度梯度成正比,比例系数K称为湍流交换系数。例如,垂直方向的通量可表示为
![]()
在湍流扩散问题中,研究的内容是计算散布在流体中的某种物质由于湍流作用所引起的输送率,即质量通量问题。根据上述湍流半经验理论的假定,同样可以假设由湍流引起的局部扩散物通量与该处扩散物质的平均浓度梯度成正比,此时的比例系数K称为湍流扩散系数,这种理论称为K理论。设扩散物质的浓度为c,垂直方向的质量通量(单位时间内通过单位面积的扩散物质量)为
![]()
负号表示质量输送方向与浓度梯度方向相反。式(4-7)就是梯度—输送理论的核心关系式,它表明湍流扩散引起的物质输送的速率同时取决于该物质分布的不均匀程度(梯度的大小)和流场自身所具有的扩散能力(K值的大小)。
4.1.1.2 湍流扩散方程
恶臭的湍流扩散方程本质上是恶臭气体的扩散满足质量守恒定律的另一种表述,因此,可以从连续方程导出,只需将流体密度ρ换成扩散物质的浓度c即可。于是考虑湍流引起的速度脉动和浓度脉动,令
![]()
将上述关系代入(4-8)并取平均,整理后
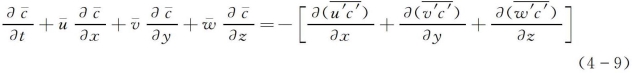
由于方程(4-9)不封闭,无法独立求解。可利用K理论将右边的未知数项用平均浓度的梯度来表示,令
![]()
代入式(4-9),得到
![]()
这便是根据K理论推导得到的湍流扩散方程。该式表明流体团中某种物质浓度的变化是由湍流扩散所引起的。为方便起见,下文中的平均浓度用c表示。
有风条件下连续点源的扩散是最常见的情形,可以对其进行简化计算。取x轴与平均风向一致,则x方向偏微分项为0。由于是定常问题,所以不考虑时间变化的影响,等式左边是关于时间的函数,由于x方向的湍流扩散项通常比平流输送项小得多,可以略去。故有风条件下连续点源的扩散方程可化为
![]()
边界条件为连续条件为
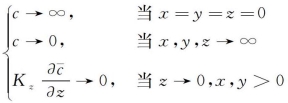
![]()
式中 Q——连续点源的源强(单位时间的释放量)。
引入恶臭湍流扩散系数K是用一种新的未知量代替原有的未知量。问题在于把K表达成气象参数与坐标变量的函数,然后在一定的定解条件下求解扩散方程。此即发展K理论大气扩散模式的起点。Kz的确定可借助近地层湍流半经验理论的研究成果,将其表示成离地高度和与风速廓线有关的函数。然而,对于Ky的求取,目前还没有一个比较令人满意的方法。
为了能对恶臭扩散方程的解有一个概略性了解,下面介绍简单条件下的求解结果。在方程(4-11)中,若Ky和Kz都是常数,则它的解是
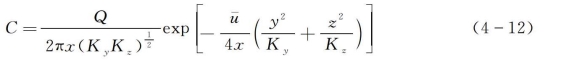 (https://www.daowen.com)
(https://www.daowen.com)
这类K为常数的恶臭扩散称为裴克扩散。从上述解的情况可以看出:①恶臭扩散的质量浓度与源强成正比;②离恶臭源越远,浓度越低;③恶臭湍流扩散系数越大,恶臭污染物浓度越低;④恶臭扩散的质量浓度在横向及垂直向均符合正态分布。
这些定性的结论与恶臭污染物扩散实验结果基本一致,然而在数值上有时会存在偏差。例如,在平坦地形小尺度扩散试验中观测到轴线上的浓度逐渐减小,但在式(4-12)中则是逐渐增大。如果用实测数据来配合式(4-12),势必要求Ky和Kz的值随着远离扩散源的距离的增大而无限增加。在非相对扩散问题中,将表征恶臭扩散能力的参数视为离源距离的函数显然是不合适的,因此不能通过假定常数K来对连续点源的扩散问题进行求解。然而,对于大尺度的恶臭扩散来说,臭气扩散所占据的空间尺度远远大于对扩散起作用的湍涡尺度。此时扩散的性质不再受到取样时间及扩散范围改变的显著影响,可采用常扩散系数模型。此外,随着扩散尺度的增大,扩散方程中扩散项的作用相对减小,因扩散系数的假定所产生的误差亦减小。因此,可利用裴克扩散模型来模拟大尺度的恶臭扩散。
将式(4-12)代入式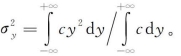 其中σy为横向浓度分布的标准差,代入标准差公式到裴克扩散的浓度方差为
其中σy为横向浓度分布的标准差,代入标准差公式到裴克扩散的浓度方差为
![]()
可见,其浓度分布的标准差与扩散的时间或质点运动距离的平方根成正比。
对于多数恶臭扩散问题都不能假定K为常数,必须根据具体的问题给出K的形式和适当的定解条件。
恶臭的瞬时点源扩散属于非定常的相对扩散问题,扩散速率随着“臭气团”的增大而增加,扩散系数不能仅凭气象条件和离地高度而事先给定,其还有赖于“臭气团”自身的扩散程度。因此,用K理论来解决瞬时恶臭源的扩散问题是十分困难的。
恶臭的连续线源扩散(大型反应池或除臭罩边界泄露)是二维定常问题。取线源方向与平均风向(x轴)垂直,于是浓度沿y轴均匀分布,只需要考虑垂直方向的扩散。扩散方程可简化为
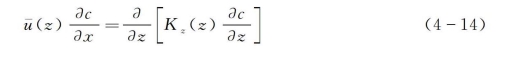
边界条件为

连续条件为
![]()
Kz是离地高度的函数,同时还取决于恶臭风速场、温度场的分布。一般情况下,Kz主要取决于风速随高度的分布。为避免风速廓线对数律在方程求解中的困难,通常采用乘幂律,即
![]()
根据恶臭湍流半经验理论,此时的Kz(z)满足共轭乘幂律
![]()
上述问题的解决取决于以下条件:①能否给出具有合理物理解释的Ky表达式。②克服数学求解的难易程度。
然而,到目前为止尚未获得令人满意的结果。从下面的讨论中可以知道,恶臭横向扩散在很大程度上与梯度输送的机理无关,因而无法客观地给出Ky,这便是问题的症结所在。
4.1.1.3 分析与讨论
恶臭扩散梯度-输送理论的缺陷来源于湍流半经验理论。这个理论将无规则的“湍涡”运动与恶臭污染物分子热运动相类比,认为前者以与恶臭污染物分子热运动过程相同的方式来完成流场中各种属性的交换和输送。事实上,这只是形式上的比拟,两者之间具有本质的不同。恶臭污染物分子运动过程以客观的分子输送模型为基础,严格导出了通量与梯度的线性关系,分子扩散系数是流体的物理属性,近似为常数。而恶臭污染物湍涡的数学模型则完全是假想的,它假定“湍涡”是具有相同属性的流体微团,在其突然产生直至突然消亡的过程中属性守恒。这样的“湍涡”实际上并不存在,在湍流混合过程中,流体微团的属性会逐渐改变。因此,根据湍涡输送模型导得的梯度与通量之间的线性关系,实质上是一种假定。
恶臭流场的性质极其复杂,湍流输送的性质远非简单的线性关系就能完全描述。在梯度—输送理论的假定下,流场性质的差别完全依赖于对比例系数K的不同假设。在许多情况下,假定的K的形式仅仅是为了计算结果与某些观测事实相符或者能带来数学处理上的方便,缺乏合理的物理解释。
上述缺陷直接导致了梯度—输送理论在实际应用中的局限性。与分子运动过程不同,湍流交换系数K不是恶臭污染物的物理属性,而是恶臭气体的运动属性。从式(4-17)可以看出,它随恶臭气体运动的性质改变,也随平均的时间尺度和空间尺度的改变而改变。
![]()
由于恶臭湍流场的性质和湍流运动的尺度都在很大范围内变化,故K的数值范围可跨越几个数量级,这大大限制了K理论的普遍性,增加了应用中的随意性和盲目性。此外,恶臭的许多扩散过程并不符合梯度-输送理论的作用机理,进一步限制了它的适用范围。
虽然梯度—输送理论存在上述缺陷,但它仍是恶臭扩散理论的主要依托,并在各类恶臭污染问题中得到广泛的应用。与其他理论比较,K理论也有一些重要的优点。例如,它能够直接利用实际的恶臭抽风风速廓线资料而不必作流场均匀假设。此外,它无须事先假定某种分布形式就可以求解出扩散物质的浓度分布。
