4.1.2 湍流扩散的统计理论
4.1.2.1 基本概念
从灵敏的测风仪观测记录可以看出，恶臭气体微团运动的速度（大小和方向）时刻都在发生着极不规则的变化。与粒子的布朗运动轨迹一样，湍流流场中恶臭气体微团的运动速度也无法被预测。正是湍流运动的这种高度随机性促使随机函数和随机场理论在湍流研究中的应用。此时研究的对象不再是个别恶臭气体微团的速度脉动，而是将它们看成一种统计系集，考察它们对流场性质的“整体”影响。
将平均抽风风向取为x轴方向，考察从原点出发的一个标记恶臭气体微团的运动。经t时间后，恶臭气体微团偏离原点的距离为x（t）。由于湍流脉动速度v'（t）的存在，恶臭气体微团在y方向会发生位移，记为y（t）。由于湍流脉动速度是随机的，恶臭气体微团的湍流运动是一个随机过程，在t时刻，y（t）可以取一切可能的数值，所以无法预测y（t）的值是多少，显然这不是该问题的统计学提法。通过多次重复相同的试验可以发现，虽然每个恶臭气体微团在y方向的位移可正可负、可大可小，但是众多恶臭气体微团位移的集合却趋于一个稳定的统计分布。也就是说，虽然无法预知单个恶臭气体微团在t时刻位移的确切数值，但能够给出它在每个位置上的概率。
设已知恶臭气体微团的概率密度函数为P，源强为Q，则浓度分布为
反之，可以通过大量的浓度分布测定来推算恶臭气体微团的概率分布。恶臭气体微团分布的方差也可以用它的概率密度函数来表示，对上述二维问题有
如果是瞬时点源，以气团的中心为原点，则
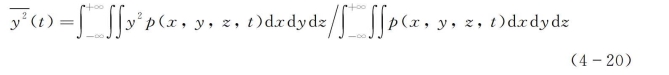
同理可得到关于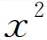
、
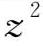的表达式，它们的均方根就是扩散参数σx、σy和σz。恶臭扩散统计理论研究的重要内容之一即是寻求恶臭气体微团的概率分布。
4.1.2.2 间歇不连续运动的恶臭扩散
概率相等的无规则行走（以下简称“无规行走”）是经典的不连续运动扩散问题，它是这样提出的：一个人前后荡步，设每步向前和向后的概率都等于1/2，问经过n步以后，他离开起点m步（前进或后退）的概率是多少？
在污泥批次处理中，经常发生间歇不连续运动的恶臭扩散，在加盖（加罩）污水处理单元，检修盖板瞬时间隙打开的工况，也属于间歇不连续运动的恶臭扩散。
这个问题可按如下方法求解：
设在n步中，向前n1步，向后n2步，于是
进一步考虑各种可能的行走方式。显然，无规行走n步的全部走法共有2n种，最终向前m步的走法等于向前n1步或向后n2步的走法，应为
其概率等于这种走法与全部走法的比值：
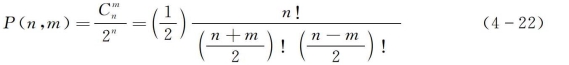
从式（4-22）可以导出两点重要的推论：
（1）当行走的步数足够多，所走距离的概率分布接近正态分布，即当n充分大时
（2）无规行走位移的均方差（相当于扩散参数）与行走时间的平方根成正比，即
根据概率分布与浓度分布的关系，如果有许多恶臭气体微团间歇按照无规行走的方式同时从原点出发，经过相当长时间以后，这些恶臭气体微团的浓度分布接近正态分布，其分布的标准差与时间的平方根成正比。虽然无规行走的模型十分简单，但它能够说明恶臭扩散统计理论的一些基本概念和方法特征。
4.1.2.3 连续运动的恶臭扩散
从前面的讨论可知，扩散统计理论的中心思路是寻求恶臭气体微团扩散关于时间和空间的概率分布，从而进一步求得扩散物质浓度在空间上的分布及其随时间的变化规律。虽然无规行走问题已得到解决，但常规污水处理流程污水水面的恶臭湍流扩散是连续性的扩散过程，其还受到气液界面动力和热力因子等各种影响，情况要比简单的无规行走问题复杂得多。在平稳和均匀湍流的假定下可以证明恶臭气体微团分布符合正态分布律。
对于给定正态分布，决定扩散性质的主要参量是浓度分布的标准差，即扩散参数。将它与湍流脉动场的统计特征量联系起来，就是适用于连续运动扩散过程的泰勒公式。
考虑t0时刻从原点出发的一个标记恶臭气体微团因脉动速度v'（t）产生的位移y（t）。经过时间t后位移为
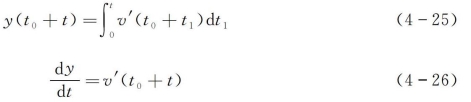
所以
由于v'和y都是随机量，对一切可能的y值统计系集取平均，根据求平均的法则，有
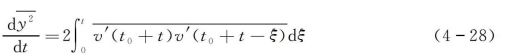
假设湍流是平稳和均匀的，上式右边的统计平均就可以用一个恶臭气体微团的时间平均来代表，且与起始时刻无关。于是由相关系数的定义得
式中 RL（ξ）——标记恶臭气体微团运动的拉格朗日相关系数。将式（4-29）代入式（4-28）有
式中 
——拉格朗日意义下的湍流强度。对上式进行积分，可以求出任意起始时刻之后T时段内恶臭气体微团位移的方差：
这就是适用于连续运动扩散过程的泰勒公式。它表示从原点出发的许多恶臭气体微团经过T时间在x方向移动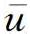
T距离以后，它们在y方向位移的方差。因此
在平稳、均匀湍流中，
还可以表示单个恶臭气体微团在T时段内不同时刻位移的方差。
泰勒公式表明，粒子湍流扩散的范围取决于湍流强度及脉动速度的拉格朗日相关性。在相同时段内，湍流强度越大、脉动速度的相关程度越高，恶臭气体微团散布的范围就越广。利用这一原理，可以通过对流场中单个恶臭气体微团运行轨迹和速度的观测推算出所有扩散的分布。
不需要对RL（ξ）的形式作任何具体的假定，就可以从泰勒公式得出两个简单的推论：
（1）T充分小时，所以RL（ξ）→1
（2）设ξ＞t1时，RL（ξ）=0，则对充分大的T（T＞t1）有
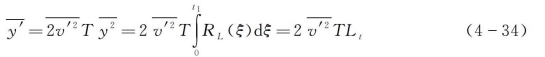
式中 Lt——湍流的拉格朗日时间尺度。可以看出，经历充分长的时间以后，连续运动的扩散同样有σy∝
的关系。这与裴克扩散和无规行走模型的结论相同。进一步证明了裴克扩散模型应用于大尺度扩散问题的合理性。
泰勒公式虽然给出了湍流脉动速度统计特征量与恶臭扩散参数之间的关系，但还不能直接用来解决恶臭气体微团的扩散问题。湍流场的性质由气象条件决定，为将上述关系发展成可应用的形式，需用可测的气象参数将拉格朗日相关系数表达出来，即导出扩散参数与气象条件之间的直接关系。这是许多统计理论模式的共同出发点。
泰勒公式是在平稳、均匀湍流的假设前提下导出的，实际大气并不满足这样的条件，其仅在地形平坦开阔、气流稳定的小尺度扩散问题中才近似成立（垂直方向的气象参数取某一层的平均值），这使得该理论的应用受到限制。
恶臭扩散统计理论不单是要找出反映恶臭污染范围的扩散参数，更重要的是寻求恶臭气体微团扩散的概率分布函数。由于恶臭湍流扩散的不平稳、不均匀条件无法从理论上导出这个函数，必须借助经验和假设，这也是发展恶臭扩散统计理论最主要的困难。目前普遍的做法是作正态分布假设，再利用泰勒公式定出标准差，从而确定污染范围内恶臭气体扩散的浓度分布。