6.3 材料的本构模型
2026年01月14日
6.3 材料的本构模型
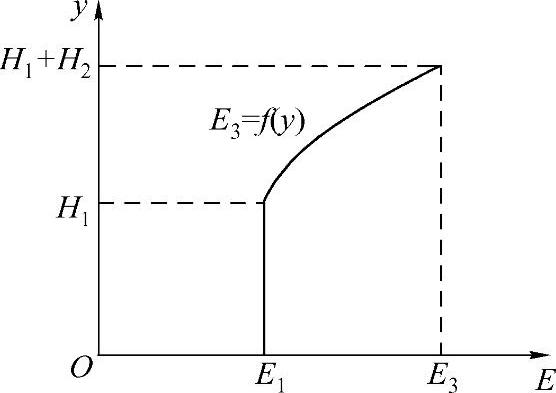
图6-2 功能梯度材料基体-涂层的 弹性模量与空间位置关系
假设功能梯度涂层材料和基体均匀材料的应力-应变关系都为线弹性本构模型,图6-2给出了功能梯度材料基体-涂层的弹性模量与空间位置的关系,由图6-2可知基体均匀材料的弹性模量不随空间位置变化,为常量E1=100GPa,功能梯度涂层材料的弹性模量为空间坐标函数,变化关系如下:

式中,βE为功能梯度材料弹性模量非均匀参数。由于弹性模量在整个涂层-基体中具有空间的连续性,因此βE与空间位置存在以下关系:

式中,E3为涂层顶部的弹性模量,本实例取值为1000GPa。基体和涂层材料的泊松比都取0.3。对于动态断裂问题,其有限元列式为:

式中,[M]为质量矩阵;[C]为阻尼矩阵;[K]为刚度矩阵;{F}为结构外载荷矢量;{uüü}为节点加速度矢量;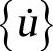 为节点速度矢量;{u}为节点位移矢量。(https://www.daowen.com)
为节点速度矢量;{u}为节点位移矢量。(https://www.daowen.com)
弹性模量和泊松比用于形成总体刚度矩阵,密度用于形成总体质量矩阵。本实例中的密度变化规律也符合指数变化规律:

式中,
βρ为功能梯度材料密度非均匀参数,由于密度在整个涂层-基体中具有空间的连续性,因此
βρ与空间位置存在以下关系:

式中,ρ1为基体密度,ρ3为涂层顶部密度。本实例中ρ1=3000kg/m3;ρ3=8000kg/m3。
