7.2.1  流体模型

7.2.1 流体模型

在本节的其余部分，首先得到合适的液滴及干燥过程中溶质的浓度的控制方程，这对于微米大小水滴是适用的。派生的起点是液滴的Navier-Stokes方程。如果假设一个不可压缩液体的液滴，流体动力学方程可以写成

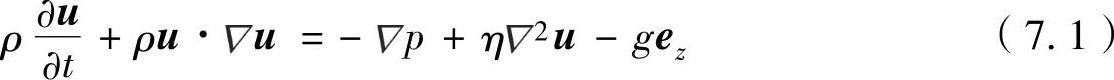
连续性方程：

·u=0 （7.2）

式中，u代表流体速度；ρ和η代表质量密度和流体动力学黏度；p代表压力；g表示重力加速度，方向为Z负方向。

不同数量级的式（7.1）和式（7.2）可以通过引入特征值来评估液滴水平方向的大小R和垂直方向液滴的大小H。合适的液滴半径和高度在最初的传播阶段之后确定。如果液体在垂直方向的标准速度等于在液滴表面的平均蒸发速度v_e，a_v，那么典型的水平速度的值等于：

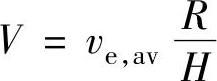
如果液滴的半径大于它的高度，所求的速度大于标准的垂直速度。因此用V标定水平速度分量，用v_e，av来标定垂直速度分量。最合适的时间表是R/V。

接下来分解速度在水平方向的分量为u_‖，垂直分量为w：u=u_‖+we_Z。通过这种方式，Navier-Stokes方程的水平速度与垂直速度的分量可写为如下形式：

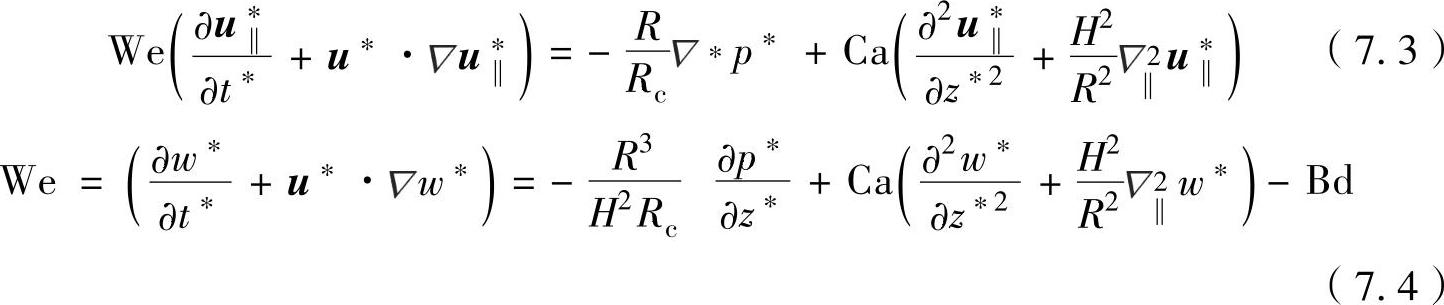
这里引用星号为缩放变量，符号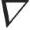_‖为梯度算子的水平分量。另外，规定Ca是毛细管数，定义为

We为韦伯数，计算公式为

Bd为Bond数，计算为

最后，R_c典型是曲率半径，σ/R_c作为压力的典型值，其中σ是表面张力。