2.4 概率抽样设计
市场往往是由不同的个体所组成的各种群体、组织所构成的。如果一个市场中的每个个体在所有方面都相同,那么抽样就没有必要了。因为只要了解一个个体的特性,就可以了解到整个目标总体的情况。但现实是构成目标市场的群体绝大多数都存在一定的差异,而概率抽样的目的就是将这些差异尽可能地通过有限的样本体现出来。
在图2-2中已经展示了概率抽样的常见方法,不同的抽取方法有着各自不同的特点。诚如前文提到的,在实际抽样过程中,抽样方法的选择受到很多因素的制约,如调研目标、调查方法、抽样框获得、研究经费、样本精度要求等。以下是常用的几种基本概率抽样方法的介绍。
2.4.1 简单随机抽样
简单随机抽样(simple random sampling),又称纯随机抽样,是从总体N个单位中逐个不放回地抽取n个单位作为样本(N>n),从而保证每次都是在所有未进入样本的单位中等概率抽取(每个抽样单位被选中的概率是相等且已知的)。例如,电视台想从所有编导中抽取15人作为样本,便可以将所有编导的姓名都写成纸条并放入盒中,则每名编导被抽取的概率既是相同的,也是已知的。
简单随机抽样获取样本常用的方法有两种,即抽签法或查阅随机数字表。上面的例子就是抽签法的简单使用,但一般我们会先对总体中的所有个体进行编号以方便后续抽取。
随机数字表也被称为乱数表,表中的数字与数字排列都是随机形成的、没有规律,其抽取方法如下:
1.将总体中所有单元编号,所有编号的位数相同(根据编号位数选择合适的随机数字表)
2.随机从数字表中的任意位置开始,向任意方向连续摘录数字
3.将得到的数字按所编号的位数分割成若干组数码,得到的数码所对应的单元即入样,将重复的数码和没有对应单元的数码去掉,直到抽足所需样本为止
一般统计类的书中都附有随机数字表,如有需要也可以通过百度图片获得符合要求的随机数字表。事实上包括SPSS在内的诸多软件也都可以根据实际需要生成(伪)随机数字表格以供调研人员使用。
简单随机抽样是其他随机抽样方法的基础,因为它最符合随机原则,且方法上简单直观、容易理解,结果可以推断既定目标总体,是概率抽样中的最基本方法。
2.4.2 系统随机抽样
虽然简单随机抽样是概率抽样的最基本方法,但它也存在很多局限,比如简单随机抽样需要将总体全部进行编号,当总体体量大时会增加工作量。而且市场调查的样本量一般至少为几百个,即使总体编号不是问题,但用抽签法或随机数字表法抽取费时费力。更重要的是简单随机抽样常常忽略总体已有的信息,从而降低样本代表性。因此,人们在简单随机抽样的基础上改进出了系统随机抽样。系统随机抽样(systematic random sampling)也叫等距抽样或机械抽样,是与简单随机抽样类似的一种等概论抽样方法。它要求将总体的每个个体编号,并按照一定顺序排列,然后按一定间隔选取样本。在市场调查实践中,系统抽样常被作为简单随机抽样的代替法使用,如使用得当,其结果基本与简单随机抽样一致。和简单随机抽样相比,系统随机抽样实施更为便捷,费用更低,成为一种常用的抽样方法。
系统随机抽样的具体步骤如下:
1.和简单随机抽样一样,使用系统抽样也需要对总体中的每个个体进行编号,且需将个体按一定顺序排列(完成抽样框)
2.利用公式计算抽样间距。决定抽样间距的公式为:
样本间距(K)=总体规模(N)/样本规模(n)
3.在总体中选择任意编号作为起点,根据样本间距(K)连续抽取符合要求的编号入样,直至达到样本量要求
以下是一次使用系统随机抽样的过程:
为了解受众对节目编排的意见,东方卫视计划从205户居民中抽取8户作为代表进行调查,如果选用系统随机抽样方法进行选取,其过程如下:
1.将205户居民从001到205编号
2.用公式决定间隔数(K=205/8≈26,四舍五入)
3.抽取第一个编号:可以随意选择起点,可以利用随机表选出,也可以主观决定起点
4.按K的值进行等距抽取
想一想,在这个案例中可能会出现什么情况?
情况一:选中的样本恰好在总体编号范围内
17、43、69、95、121、147、173、199
情况二:起始编码很大,导致按间隔抽选时,会出现超出编号的可能
137、163、189、215、241、267、293、319
第一种情况直接符合我们的要求,而当出现第二种情况时(编码超出了总体规模),则应把超出部分分别减去N,然后入样:
137、163、189、215(10)、241(36)、267(62)、293(88)、319(114)
根据这两种抽样状况,想一想当我们在实际抽样时,如果选用了系统随机抽样方法,如何操作会更便利一些?
调研人员往往会因为系统随机抽样的经济性、操作便捷性,以及时间和费用成本都相对较少而选用它。在使用过程中要注意避免样本框中的固有周期性分布与样本间距重合。比如央视索福瑞计划采用系统随机抽样的方法对湖南卫视全年收视情况进行调查,他们打算从湖南卫视全年365天中抽取一定量天数的收视率进行观察,如果他们计算出的间距为7,则抽取的结果将无法代表总体的全部情况,从而导致结论存在严重偏差。想一想为什么?
2.4.3 分层抽样
分层抽样(stratified random sampling),又称类型抽样,是先将总体所有单位按某些重要特征分成若干互不重叠的子总体(层),然后在各个子总体中采用简单随机抽样或随机抽样(抽取方法一般按各层占总体的比例)。在实践中,我们不可能在展开调研前对目标总体一无所知,所以分层抽样弥补了简单随机抽样忽略已知对象特征的不足而常被采用。其实施过程一般分为三个步骤:
1.将目标总体按已知特性分为几个同质子集(层)
2.根据各同质子集在目标总体中所占比例,在各层随机抽取样本
3.将从各层抽取的样本合并为目标总体的样本
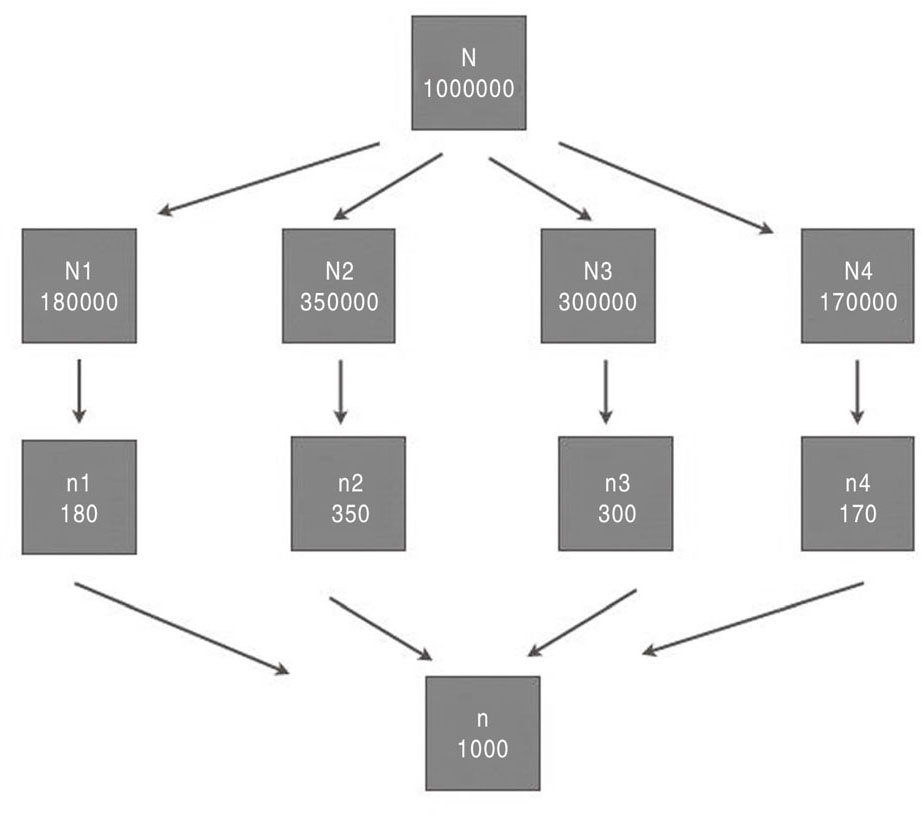
图2-3 分层抽样
图2-3是一个目标总体为1000000的分层抽样示例,其中N1、N2、N3、N4即按照已知特性进行划分的4个同质子集。
比如调研人员要研究某类节目题材在某地区的市场潜力,他们会将该地区的居民按照一定的标准划分成为不同的层(如按照收入水平、人口密度、地理位置、有线电视入户密度等)。
相较于前两种概率抽样,分层抽样使得样本更易具代表性,并可以根据需要对各层特性加以比较,从管理和实施上比简单随机抽样方便。但如果想让分层抽样效果最大化,分层标准的选择就变得非常重要,其总体原则:
不同层内差异要小
层与层间差距要大
抽样框中有该标准(指标)
通常情况下,分层越多,结果的准确性就会越高。但如果分层的标准没有意义,则只会浪费时间和经费,而不会有任何价值。
分层抽样在抽取过程中也可以不按照各层所占比例进行样本抽样(即比例分成抽样,proportionately stratified sampling),而是根据各层对于调研目标的重要程度进行抽取,这种方法被称为非比例分层抽样(disproportionately stratified sampling)。
2.4.4 整群抽样
整群抽样(cluster sampling)类似于分层抽样,它是一种将总体划分为若干个不重叠的群,假定每个群内都包含目标总体的所有特性,因此每个群容量相等。然后在所有的群中再随机抽取若干个群,对抽中的这些群内的所有个体或单元全部进行调查的抽样方法。最常见的整群抽样是地区抽样(area sampling)。在地区抽样中,群是按照地理特征划分的。在抽取过程中可以使用任何既存的地理信息,如省、市、区县、街道、栋等。
整群抽样性价比高且易于实施,调研人员可以根据已有样本框特征(如地理信息)快速确定调查对象。但整群抽样可能会出现群类同质性问题,因为同质性越高,则越不符合前提假设所要求的能够代表目标总体的所有特性,则样本的准确性就越差。
2.4.5 多级抽样
多级抽样(multistage sampling)又被称为多段抽样或分段抽样,一般常用二级抽样。它是按抽样元素的层次关系,将抽样过程分为几个阶段进行。先抽取大的单元,再在大的单元中抽小的单元,再在小的单元中抽更小的单元……直至抽取到最基本的抽样单元为止。多级抽样一般适用于范围大、总体对象多且复杂的大型市场调查,但误差较大。
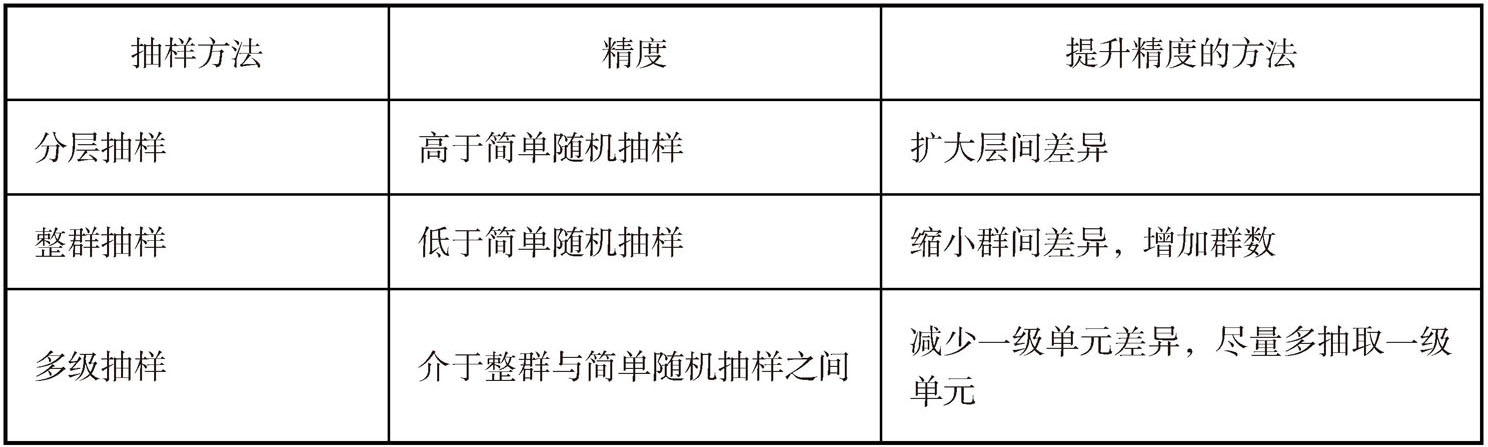
在样本量相同的前提下,我们将分层抽样、整群抽样和多级抽样做了一些比较并给出了一些建议(见表2-3)。
表2-3 三种抽样方法比较