9.6 讨论与延伸
1.延伸1:茎叶图
茎叶图(stem-and-Leaf display)又称枝叶图,是一种显示数据的图形化方法。当数据量不是太大时,茎叶图十分有用。假设我们获得了2020年中超联赛16支球队的成功长传次数如下:
58,53,53,52,39,38,33,32,32,31,30,30,29,28,16,9
我们可以将它转化成茎叶图:
5| 8,3,3,2
3| 9,8,3,2,2,1,0,0
2| 9,9,8
1| 6
0| 9
|左边部分是茎。本例中它们是数字5、3、2、1和0,在图形左侧以柱状结构排成一列。把这些数字想象成是10的倍数。例如,3就是用来表示30到39中任意一个以3开头的数字。|右边的数字是叶节点,每一个数字分别代表个位数字。因此,图中的每一片叶子都代表将叶子加到其茎的10倍值上之后的结果。
茎叶图和直方图类似,但又存在明显差异,请思考茎叶图的优势有哪些。
2.延伸2:箱线图
箱线图(box-plot)又称箱形图、盒须图,是一个基于最小值、第一四分位数、中位数、第三四分位数和最大值所形成的图形。由于此图形看起来像一个矩形,并有从顶部和底部延伸的线,故被称为箱线图。
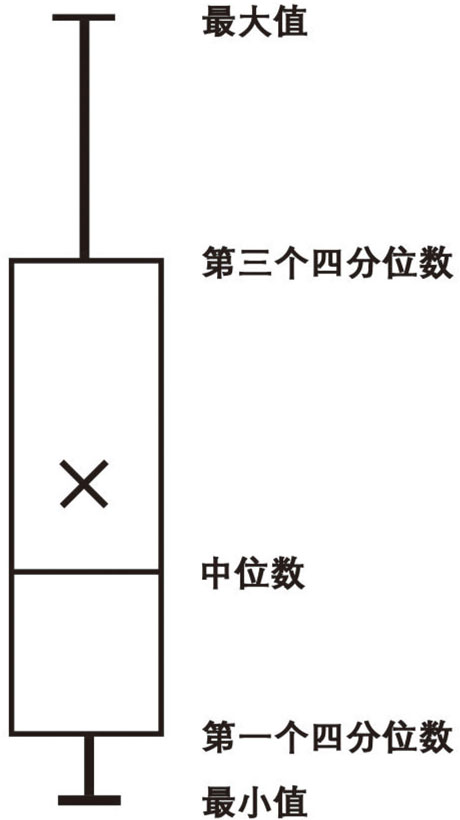
在一个典型的箱线图中,矩形的顶部表示第三个四分位数,靠近矩形中间的水平线表示中间值,矩形的底部表示第一个四分位数。从矩形的顶部延伸出一条垂直线来表示最大值,从矩形的底部延伸出另一条垂直线来表示最小值。图示显示了一个箱线图的通用示例,其中标记了最大值、第三个四分位数、中位数、第一个四分位数和最小值。横线之间的相对垂直间距反映比例值。
3.延伸3:双尾检验与单尾检验
通常假设检验的目的是为了得到总体参数是否相等,以两样本均数比较为例:
原假设为两样本所代表的总体均数相等;
备择假设为不相等(即有可能甲大于乙,也有可能甲小于乙)。
通常做这样的假设可能是因为研究人员没有充分的理由判断甲所代表的总体均数会大于乙的或甲的会小于乙,或者是因为根据研究目的,研究人员只关心甲乙两个样本各自所代表的总体均数是否相等,至于哪个大哪个小,他们并不关心,这时往往会采用双尾检验。
如果研究人员基于经验或专业知识判断甲所代表的总体均数不可能大于(或小于)乙,这时一般就采用单尾检验。
