4.1.2　质量排名算法的性能指标

4.1.2　质量排名算法的性能指标

针对质量排名的评价指标有平均倒排名次（Mean Reciprocal Rank，MRR）、Kendall τ、斯皮尔曼（Spearman）等级相关度以及DeltaAvg。

一、平均倒排名次MRR

平均倒排名次MRR的计算公式如下：

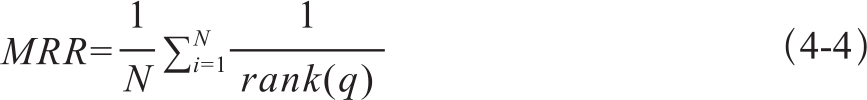
N为总排名数。评测系统返回的排名次序和正确的次序进行比较，可计算MRR。例如，系统返回的某译文的质量排名，如果正确排名为第4，那么倒数排序值为1/4。如果返回排名中不包含正确答案，那么得分为0。系统评测的排名性能是对所有译文排名结果的平均值。

二、Kendall τ

Kendall τ为等级相关系数，用于反映分类变量相关性的指标，适用于两个分类变量均为有序分类的情况。近年来在排序式的机器翻译评价中常用Kendall τ指标衡量算法的性能，其取值范围在［-1，1］之间。Kendall τ指标的计算方法为：

设随机变量X＝（x₁，x₂，…，x_n），Y＝（y₁，y₂，…，y_n），其中（x_i，y_i）表示第i个观察值对，x_i、y_i的值具有唯一性。两个观察值对（x_i，y_i）和（x_j，y_j）（i≠j），当两个元素的排名相同时称为一致，即当x_i＞x_j，时，y_i＞y_j；当x_i＜x_j时，y_i＜y_j。其他两种情况称为不一致，即当x_i＞x_j时，y_i＜y_j；当x_i＜x_j时，y_i＞y_j。但是当x_i＝x_j或y_i＝y_j时就不是一致，也不是不一致。Kendall τ相关系数定义为式4-5：

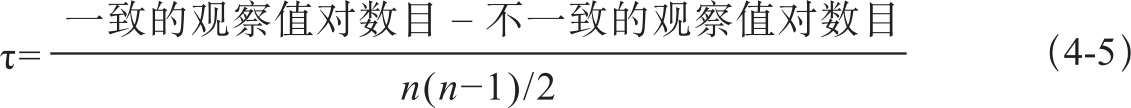
如果两个变量完全一致，Kendall τ的值为1，反之，如果两个变量完全不一致，Kendall τ的值为-1。当两个变量独立时，Kendall τ为0。

由于因x_i＝x_j或y_i＝y_j时，不计算观察值的对数，为了保证Kendall τ的值仍然在［-1，1］之间，需要对等级相同时进行修正，因此存在多个Kendall τ系数，如Kendall τ－a，Kendall τ－b，Kendall τ－c，具体不详细介绍了。

三、斯皮尔曼等级相关度

斯皮尔曼（Spearman）相关度是根据等级数据研究两个变量间相关关系的方法。它是依据两列成对等级的各对等级数之差来进行计算的，所以又称为“等级差数法”。斯皮尔曼等级相关度的定义为：

设两个随机变量X＝（x₁，x₂，…，x_n），Y＝（y₁，y₂，…，y_n），其中x_i、y_i表示第i个取值。分别对X和Y中的值排序，得到两个元素排名集合X、Y，其中元素x_i、y_i分别为x_i在X中的排名以及y_i在Y中的排名。将集合X、Y中的元素对应相减得到一个排行差分集合D，其中d_i表示x_i－y_i，那么随机变量X、Y的Spearman等级相关系数ρ可由D计算而得，形如式4-6：

斯皮尔曼等级相关度对数据条件的要求没有积差相关系数那么严格，只要两个变量的观测值是成对的等级评定资料，或者是由连续变量观测资料转化得到的等级资料就可以，不论两个变量的总体分布形态、样本容量的大小如何，都可以用斯皮尔曼等级相关来进行研究。

四、DeltaAvg

DeltaAvg是近年来提出的用于排名的评测指标（Callison-Burch et al.，2011），用于评测一个假设排序结果（hypothesis ranking）参照人工外部打分的价值度。

给定一个译句s，V（s）表示s的外部评分。如果用S表示句子集合，那么V（S）表示所有句子得分的平均值。对一个已经根据质量得分排序的由n个句子构成的集合S，S₁表示集合的第1个分位数（the first quantile of set S），S₂表示第2个分位数，以此类推，S_n表示第n个分位数。如果不能被n等分时，最后一部分包含剩余的部分。另外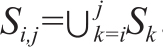，，表示i-j分位点的集合。那么分位数为n时，DeltaAvg的定义为：

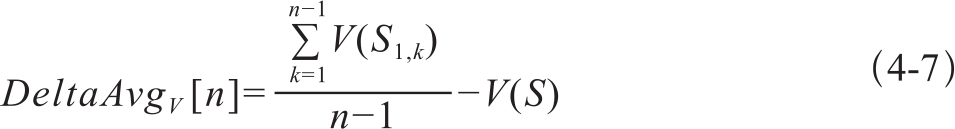
从2到N变化分位数，最后得到一个平均值作为DeltaAvg得分如式4-8：

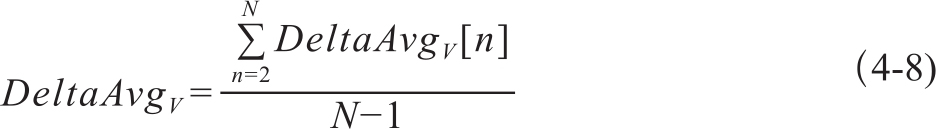
其中N＝|S|/2。

根据研究结果（Callison-Burch et al.，2011），DeltaAvg指标和Spearman排序结果高度相关。该指标的优点是它是一个无参数估计，具有确定性和一致性，DeltaAvg的结果具有可解释性，比如得分为0.5表示排名在前面分位数的结果和整体质量之间的差距为0.5。