5.2.2　搭配错误

5.2.2　搭配错误

一、搭配关系

词汇的固定搭配体现了语言应用的一些定式。比如“红茶”在英文中应该翻译为“black tea”，而非字面对译的“red tea”，“一群蜜蜂”译为“a swarm of bees”而不是“a crowd of bees”。更不用说一些习语和成语的翻译，其词汇之间的关系更加紧密，不可随意替换。尽管语言学界对于什么是搭配并没有确定而且统一的定义，但我们认为在翻译中，一些词不能随机组合在一起，虽然表面看也是符合语法要求的。从计算数据角度看，搭配词之间的分布和与其他没有搭配关系的词的分布是不同的，这可以从大规模语料中得到验证。当然，这个信息也被当作检查是否搭配正确的依据之一。

常见的搭配结构出现在：

·　形容词和名词的搭配：如：浓茶（strong tea）

·　动词和名词的搭配：如：做决定（make a decision）

·　名词和名词的搭配：如：电影院（movie theatre，不是film theatre）

·　副词和动词的搭配：如：彻底逗乐（thoroughly amuse）

二、错误检查的统计指标

词汇分布的统计量经常用于检查词汇之间是否存在搭配关系。检查词汇分布差异的数学指标有：

（1）卡方检验（chi-square test）

统计假设检验是根据观察结果来验证词汇之间的共现是随机的还是存在一定的关联关系。卡方检验的基本思想是：首先假设无效假设H₀成立，当H₀成立，计算出χ²值，该值表示观察值与理论值之间的偏离程度。根据χ²分布及自由度可以确定在H₀假设成立的情况下当前统计量发生的概率P。如果P值很小，说明观察值与理论值偏离程度太大，应当拒绝H₀假设，表示比较数值间存在显著差异；否则就接受H₀假设，不认为样本所代表的情况和理论假设存在差异。

下面是一个用卡方检验检查存在搭配关系的例子。设有两个单词w₁、w₂，其二元组w₁w₂是否构成搭配关系？首先在实际语料中的统计w₁、w₂和w₁w₂的发生次数，还有w₁、w₂分别和其他词共现的次数，表示为w₁w₂、w₁w₂。假设我们从大规模语料中得到上面这些数值如表5-2所示：

表5-2　w₁、w₂和w₁w₂的观察数值

那么，根据极大似然估计可得到：

P（w₁）＝50/500＝0.1

P（w₂）＝25/500＝0.05

P（w₁w₂）＝20/500＝0.04

无效假设H₀为：单词w₁、w₂相互独立，不存在搭配关系

假设H₀成立，那么就有：

P（w₁w₂）＝P（w₁）*P（w₂）＝50/500*25/500＝0.005

也就是二元组w₁w₂的期望概率应该为0.005，在上面语料中对应的发生次数应为0.005*500＝2.5。其他概率期望值同样可以计算出来，如表5-3：

表5-3　w₁，w₂和w₁w₂的期望值

卡方值的计算式如式5-1：

根据上面两个表的数据不难计算出卡方检验的结果为：

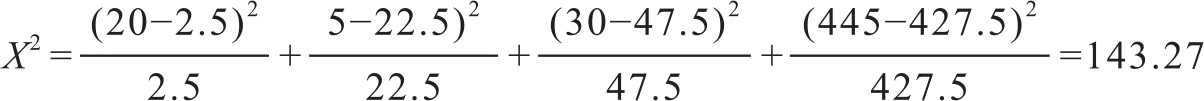
查自由度为1的卡方检验表，可以得到假设H₀成立的概率为0.001。因此，我们有理由拒绝假设的成立，认为单词w₁、w₂存在关联关系，也就是构成搭配关系。

（2）互信息

互信息（Mutual Information，MI）是信息论中的概念，最初用于通信领域。在检查搭配关系时，我们将单词视为一个点，用的是点对点的互信息（Pointwise MI，PMI）。计算公式为5-2：

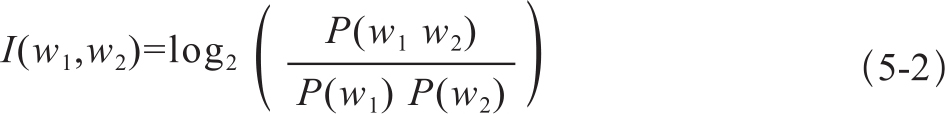
根据上例中的数据可得单词w₁，w₂的互信息值为：

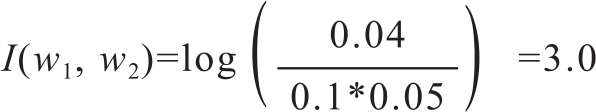
这个互信息值的含义是：当已知单词w₁出现时，单词w₂出现的不确定性降低的数量。很明显，如果w₁、w₂相互独立，那么P（w₁w₂）和P（w₁）*P（w₂）相等，将导致对数结果为0。也就是说，互信息值越大，w₁、w₂越有可能构成搭配关系。但是Manning et al.（1999）也指出，互信息方法用于搭配关系容易受到数据稀疏的影响，在大规模数据集上的效果更好。

（3）log似然比率检验

Dunning（1993）针对低频现象提出了比卡方检验更稳定的估计检验，称为log似然比率检验（log likelihood ratio test）。当发生频率较高时，log似然比率检验的结果和卡方检验相近，低频时log似然比检验更好。但是，当发生频率低于1次时，两种检验都不能使用。log似然比率检验的计算公式为5-3：

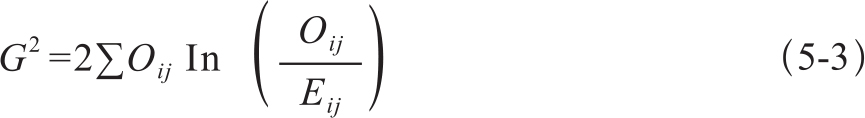
（4）基于排名比率的方法

基于排名比率（rank ratio）的方法检查搭配关系是一种无参数的方法，不需要独立性假设的前提，还能检查两个词以上的搭配关系。

要计算排名率，首先统计出目标词与上下文词组成的词串在语料中的发生频次，并根据频次由高到低排序。这个排序相当于一个有条件排名，也就是在目标词出现的上下文中的排名。然后，将目标词替换为一个通配符*，再次统计并对匹配上的词串依据发生频次排序。这次排序相当于无条件排名，也就是在不一定含有目标词的上下文环境中统计词串的发生频次。将这两个频次相比，得到排名比率。这个排名比率反映出含有目标词和不含有目标词的上下文的显著程度。对于由多个词构成的搭配，计算出每个词作为目标词的排名比率后，再用几何平均组合所有词的排名比率作为整体搭配的公共排名比率。

Deane（2005）的研究表明，该方法可有效地发现大规模语料中的多词表达式（multi-word expression）。

三、搭配错误检查的实现步骤

发现译文中的搭配错误是十分困难的任务。早期的研究尝试了基于知识源的做法。首先收集学习者常见的错误搭配，一般也是研究特定有限的搭配结构形式，比如动词＋名词、形容词＋名词等的搭配错误，形成一个数据库。检查搭配错误的步骤就是从译文中检索，有没有出现相同类型的不可接受的搭配（Shei & Pain，2000）。

很多搭配错误检查的思路是用“替换”的方法，实现包括两步：

第一步，要构造目标搭配关系的句法结构以及该搭配中其他相似的可选词。相似词的选择一般基于大规模语料或Wordnet、Roget同义词词典等资源，目标搭配的句法结构类型可以事先规定一些结构，如名词＋名词结构、动词＋名词结构、形容词＋名词结构等。

第二步，在译文中检索特定的句法结构，如果出现目标结构的搭配，就计算相应的数学指标，如排名比率等，根据设定的经验阈值判断该搭配是否可接受。如果指标很低或者在其他语料中没有出现过类似的搭配，就用相似的可选词汇替换其中的某个单词，然后再计算替换后搭配的指标，如果大于阈值或能够更好地满足上下文条件，就标注原来的搭配为错误，否则不识别为搭配错误。

该方法研究中效果比较显著的来自Chang et al.（2008）。他们基于英汉词典和英汉双语语料构建了词表（wordlist），并结合了中国学习者受母语影响而经常引发的错误搭配，如中文中“吃药”，会影响学生在译文中出现“eat the medicine”这样的动词和名词的搭配错误，而正确的搭配应该是“take the medicine”。在替换时，遇到“eat”会尝试替换为“take”并放到大规模本族语语料库中验证，判断这样替换后的搭配是否更合理。他们在200个正确搭配和226个错误搭配上的测试结果表明，搭配错误检查的准确率达到98％，召回率为91％。

用“替换”方法检查搭配错误的方式尽管比较机械，但对一些常犯的搭配错误还是比较有效。