2013年全国硕士研究生入学统一考试试题

2013年全国硕士研究生入学统一考试试题

一、选择题：第（1）～（8）小题，每小题4分，共32分.下列每题给出的四个选项中，只有一个选项符合题目要求.

（1）当x→0时，用o（x）表示比x高阶的无穷小，则下列式子中错误的是

（A）x·o（x²）=o（x³）. （B）o（x）·o（x²）=o（x³）.

（C）o（x²）+o（x²）=o（x²）.（D）o（x）+o（x²）=o（x²）.

[ ]

（2）函数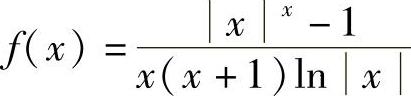的可去间断点的个数为

（A）0. （B）1. （C）2. （D）3.

[ ]

（3）设D_k是圆域D={（x，y）|x²+y²≤1}位于第k象限的部分，记I_k=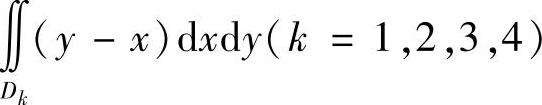，则

（A）I₁>0.（B）I₂>0.（C）I₃>0.（D）I₄>0.

[ ]

（4）设{a_n}为正项数列，下列选项正确的是

（A）若a_n>a_n+1，则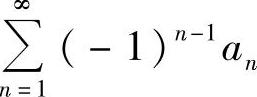收敛.

（B）若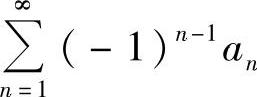收敛，则a_n>_an+1.

（C）若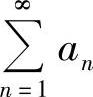收敛，则存在常数p>1，使limn^pa_n存在.

n→∞

（D）若存在常数p>1，使limn^pa_n存在，则

n→∞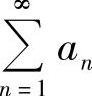收敛.

[ ]

（5）设A，B，C均为n阶矩阵，若AB=C，且B可逆，则

（A）矩阵C的行向量组与矩阵A的行向量组等价.

（B）矩阵C的列向量组与矩阵A的列向量组等价.

（C）矩阵C的行向量组与矩阵B的行向量组等价.

（D）矩阵C的列向量组与矩阵B的列向量组等价.

[ ]

（6）矩阵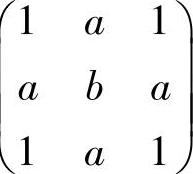与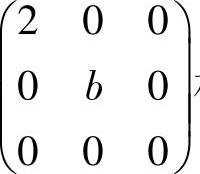相似的充分必要条件为

（A）a=0，b=2.（B）a=0，b为任意常数.

（C）a=2，b=0.（D）a=2，b为任意常数.

[ ]

（7）设X₁，X₂，X₃是随机变量，且X₁～N（0，1），X₂～N（0，2²），X₃～N（5，3²），P_j=P（-2≤X_j≤2）（j=1，2，3），则

（A）P₁>P₂>P₃.（B）P₂>P₁>P₃.（C）P₃>P₁>P₂.（D）P₁>P₃>P_2.

[ ]

（8）设随机变量X和Y相互独立，且X和Y的概率分布分别为

则P（X+Y=2）=

[ ]

二、填空题：第（9）～（14）小题，每小题4分，共24分.

（9）设曲线y=f（x）与y=x²-x在点（1，0）处有公共切线，则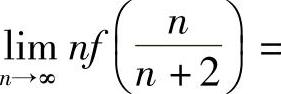

.

（10）设函数z=z（x，y）由方程（z+y）^x=xy确定，则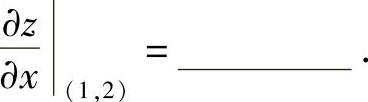

（11）

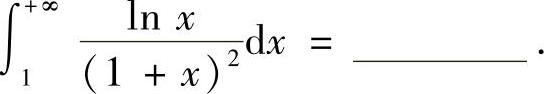
（12）微分方程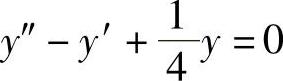的通解为y=____.

（13）设A=（a_ij）是3阶非零矩阵，|A|为A的行列式，A_ij为a_ij的代数余子式，若a_ij+A_ij=0（i，j=1，2，3），则|A|=____.

（14）设随机变量X服从标准正态分布N（0，1），则E（Xe^2X）=____.

三、解答题：第（15）～（23）小题，共94分.解答应写出文字说明、证明过程或演算步骤.

（15）（本题满分10分）

当x→0时，1-cosx·cos2x·cos3x与axⁿ为等价无穷小，求n与a的值.

（16）（本题满分10分）

设D是由曲线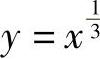、直线x=a（a>0）及x轴所围成的平面图形，V_x，V_y分别是D绕x轴，y轴旋转一周所得旋转体的体积，若V_y=10V_x，求a的值.

（17）（本题满分10分）

设平面区域D由直线x=3y、y=3x及x+y=8围成，计算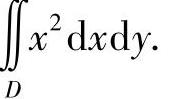

（18）（本题满分10分）

设生产某产品的固定成本为6000元，可变成本为20元/件，价格函数为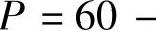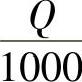（P是单价，单位：元，Q是销量，单位：件），已知产销平衡，求：

（Ⅰ）该商品的边际利润；

（Ⅱ）当P=50时的边际利润，并解释其经济意义；

（Ⅲ）使得利润最大的定价P.

（19）（本题满分10分）

设函数f（x）在[0，+∞）上可导，f（0）=0，且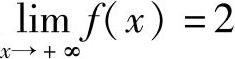，证明：

（Ⅰ）存在a>0，使得f（a）=1；

（Ⅱ）对（Ⅰ）中的a，存在ξ∈（0，a），使得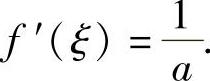

（20）（本题满分11分）

设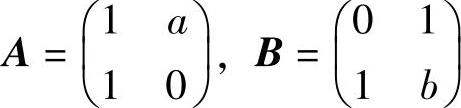，当a，b为何值时，存在矩阵C使得AC-CA=B，并求所有矩阵C.

（21）（本题满分11分）

设二次型f（x₁，x₂，x₃）=2（a₁x₁+a₂x₂+a₃x₃）²+（b₁x₁+b₂x₂+b₃x₃）²，

记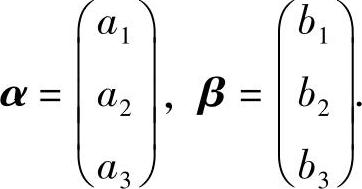

（Ⅰ）证明二次型f对应的矩阵为2αα^T+ββ^T；

（Ⅱ）若α、β正交且均为单位向量，证明f在正交变换下的标准形为2y²₁+y²_2.

（22）（本题满分11分）

设（X，Y）是二维随机变量，X的边缘概率密度为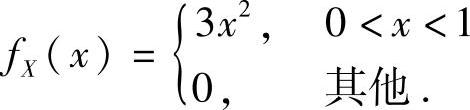，在给定X=x（0<x<1）的条件下，Y的条件概率密度为，

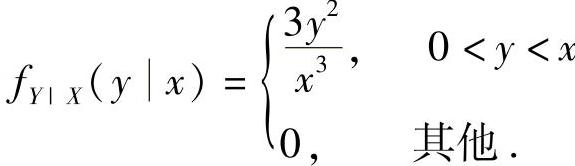（Ⅰ）求（X，Y）的概率密度f（x，y）；

（Ⅱ）求Y的边缘概率密度f_Y（y）；

（Ⅲ）求P（X>2Y）.

（23）（本题满分11分）

设总体X的概率密度为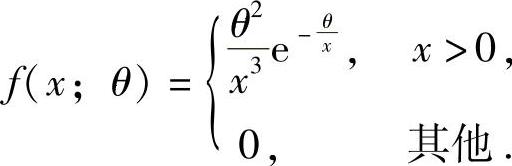其中θ为未知参数且大于零，X₁，X₂，…，X_n为来自总体X的简单随机样本.

（Ⅰ）求θ的矩估计量；

（Ⅱ）求θ的最大似然估计量.