2005年全国硕士研究生入学统一考试试题精解
一、填空题
(1)分析 用x→∞时的等价无穷小代替,即得所求的极限值.
精解 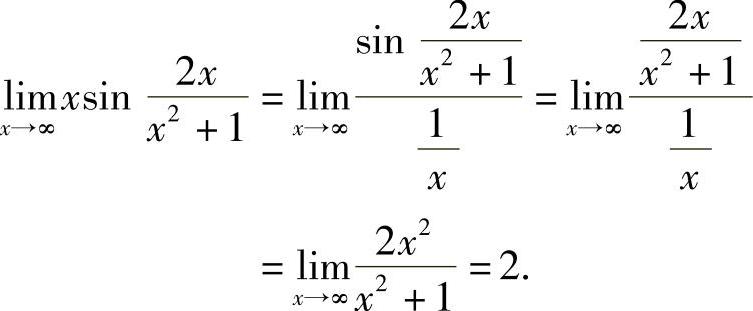
附注 所给极限写成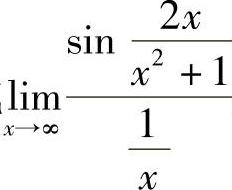 后才能用等价无穷小代替.
后才能用等价无穷小代替.
(2)分析 先算出通解,再求满足y(1)=2的特解.
精解 所给微分方程可以改写成
(xy)′=0,
所以它的通解为xy=C.将y(1)=2代入得C=2.所以所求的特解是xy=2.
附注 本题也可用变量可分离微分方程或一阶线性微分方程方法求解,但用本题方法求解更为简捷.
(3)分析 可按全微分形式不变性计算dz,然后将点(1,0)代入即可.
精解 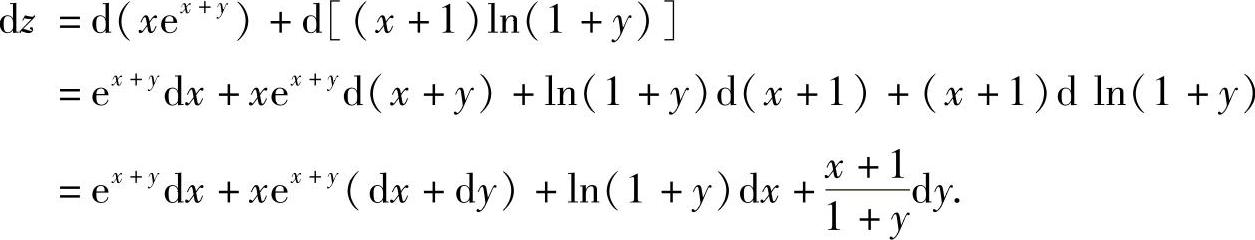
将x=1,y=0代入上式得
dz|(1,0)=edx+e(dx+dy)+2dy
=2edx+(e+2)dy.
附注 本题也可按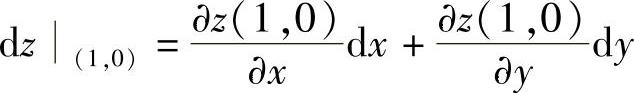 计算,其中
计算,其中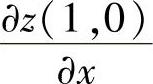 和
和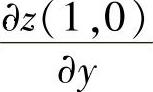 按偏导数定义计算,具体如下:
按偏导数定义计算,具体如下:
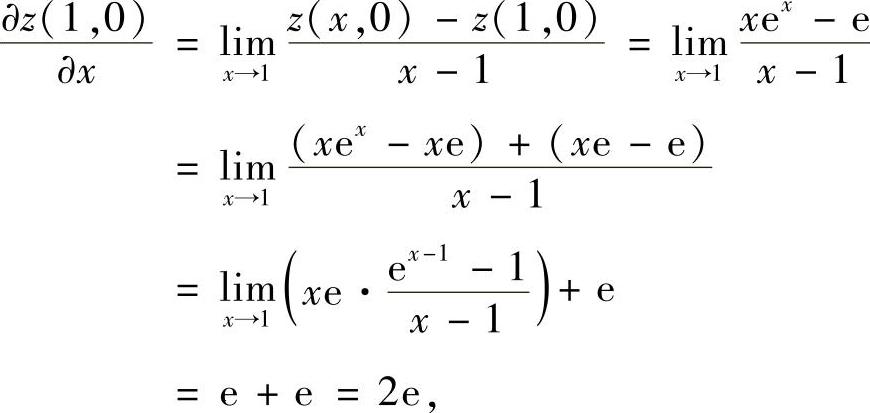
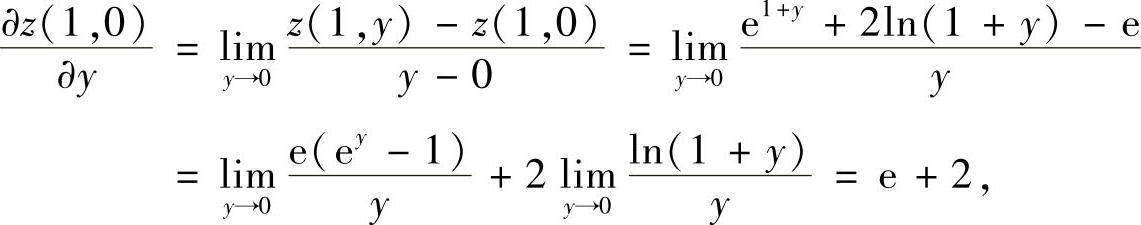
所以
dz|(1,0)=2edx+(e+2)dy.
(4)分析 记4个行向量构成的矩阵为A,则由|A|=0,即可算a的值.
精解 记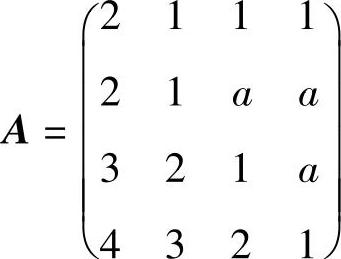 ,则由所给的行向量组线性相关得
,则由所给的行向量组线性相关得
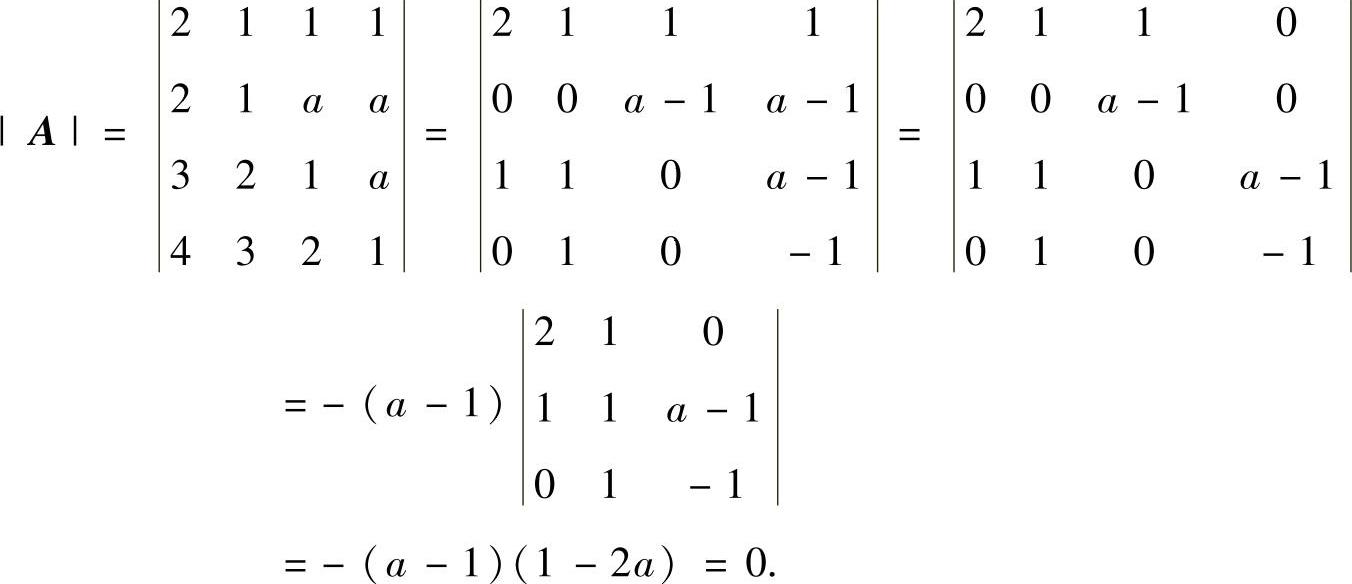
于是,由a≠1得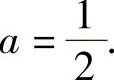
附注 当由向量组的线性相关性来确定向量中所包含的未知常数值时,如果向量组的维数与向量组的向量个数相等,则应由这一向量组为行向量或列向量构成的矩阵的行列式入手.
(5)分析 用全概率公式计算P(Y=2).
精解 {X=1},{X=2},{X=3},{X=4}是与事件{Y=2}有关的一个完全事件组,所以由全概率公式得
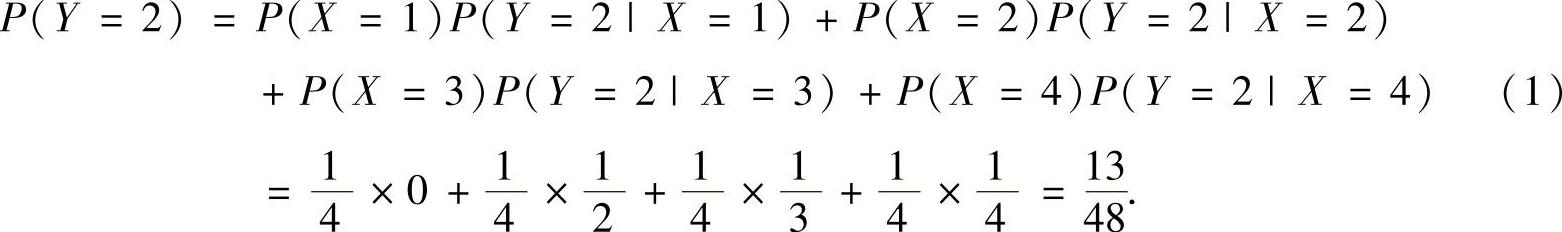
附注 用全概率公式计算随机事件B的概率P(B)时,应找到一个与B有关的完全事件组A1,A2,…,An,且P(Ai)>0(i=1,2,…,n),题中的{X=i}(i=1,2,…,4)是一个完全事件组,但{X=i}(i=2,3,4)不是完全事件组,所以在式(1)中P(X=1)P(Y=2|X=1)这一项不能省去.
(6)分析 利用二维离散型随机变量的概率分布性质及{X=0}与{X+Y=1}相互独立,可以确定a、b的值.
精解 首先由随机变量(X,Y)的概率分布性质知
0.4+a+b+0.1=1,即a+b=0.5.(1)
其次,由{X=0}与{X+Y=1}相互独立知
P(X=0,X+Y=1)=P(X=0)P(X+Y=1).(2)
其中,P(X=0,X+Y=1)=P(X=0,Y=1)=a,
P(X=0)=0.4+a,
P(X+Y=1)=a+b.
将它们代入式(2)得
a=(0.4+a)(a+b).(3)
由式(1)、式(3)得a=0.4,b=0.1.
附注 要记住离散型随机变量的概率分布的性质.
一维情形:设随机变量X的概率分布为P(X=xi)=pi(i=1,2,…),则
pi>0(i=1,2,…)且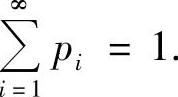
二维情形:设二维随机变量(X,Y)的概率分布为P(X=xi,Y=yj)=pij(i=1,2,…;j=1,2,…),则
pij≥0(i=1,2,…;j=1,2,…)且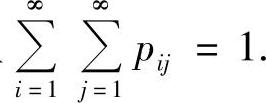
二、选择题
(7)分析 计算f′(x)的零点,然后列表确定函数f(x)的单调性,并得出正确的选项.
精解 f′(x)=6(x2-3x+2)=6(x-1)(x-2),它有零点x=1,2,据此列表如下:

由表可知,当a=2时,f(x)只有一个零点,因此选项(A)不正确.当a=4时,f(x)有两个不同的零点.
因此本题选(B).
附注 (ⅰ)本题判断零点所用的结论是:
设函数g(x)在[a,b]上连续(当a=-∞,或b=+∞时,区间[a,b]自然去掉相应的端点),在(a,b)内单调,则当g(a)g(b)<0时g(x)在[a,b]上有唯一零点.
(ⅱ)由上列的表也可算出使f(x)恰有两个不同零点的所有a值.
使f(x)恰有两个不同零点的a应满足:
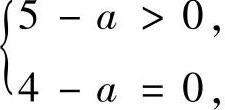 或
或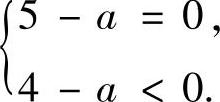
由此即得所有的a=4或5.
本题是综合题,有关内容及计算方法见提高篇05.
(8)分析 由于I1,I2,I3都是D上的二重积分,所以只要比较被积函数在D上的大小即可确定三个重积分之间的大小关系.
精解 在D上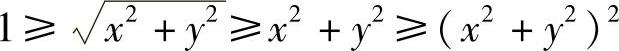 ,而cosu在[0,1]上是u的单调减少函数,所以在D上有
,而cosu在[0,1]上是u的单调减少函数,所以在D上有
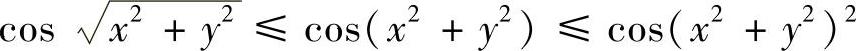 (仅在点(0,0)处取等号).
(仅在点(0,0)处取等号).
由此得到
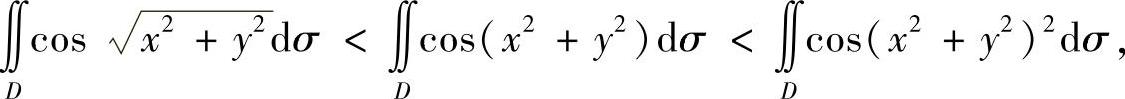
即 I3>I2>I1.
因此本题选(A).
附注 以下结论是有用的:
(ⅰ)设连续函数f(x,y),g(x,y)在D上满足f(x,y)≤g(x,y),则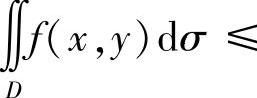
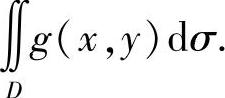
(ⅱ)设连续函数f(x,y),g(x,y)在D上满足f(x,y)≤g(x,y),且在D上至少有一点(x0,y0),使得f(x0,y0)<g(x0,y0),则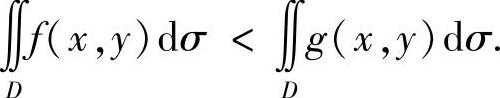
(9)分析 由于级数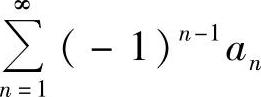 收敛,所以从它入手,并利用收敛级数性质进行考虑.
收敛,所以从它入手,并利用收敛级数性质进行考虑.
精解 由于级数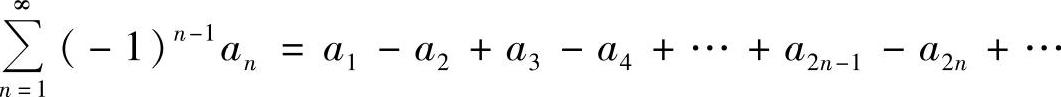 收敛,所以对它两项两项地加括号所成的级数
收敛,所以对它两项两项地加括号所成的级数
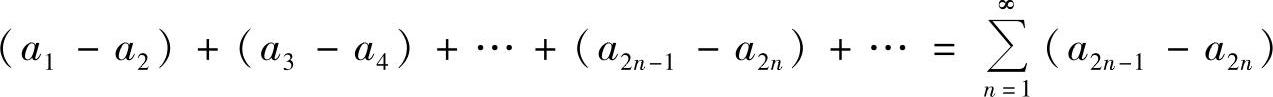
仍收敛.
因此本题选(D).
附注 以下结论是有用的:
(ⅰ)如果级数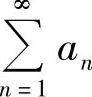 收敛,则对它的项任意加括号后所成的级数仍收敛,且其和不变.
收敛,则对它的项任意加括号后所成的级数仍收敛,且其和不变.
(ⅱ)如果对级数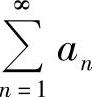 的项加括号后所成的级数发散,则
的项加括号后所成的级数发散,则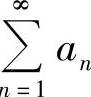 发散.
发散.
(10)分析 由于函数f(x)二阶可导,所以可用函数极值的第二充分条件解本题.
精解 由
f′(x)=sin x+xcos x-sin x=xcos x,
f″(x)=cosx-xsin x
可知,x=0,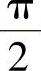 都是函数f(x)的驻点,并且f″(0)=1>0,
都是函数f(x)的驻点,并且f″(0)=1>0,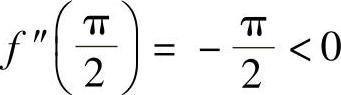 ,所以f(0)是f(x)的极小值,
,所以f(0)是f(x)的极小值,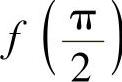 是f(x)的极大值.
是f(x)的极大值.
因此本题选(B).
附注 本题也可由函数极值的第一充分条件求解.
由于当x∈(-δ,0)时,f′(x)<0;x∈(0,δ)时,f′(x)>0,所以f(0)是f(x)的极小值.
由于当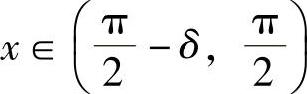 时,f′(x)>0;
时,f′(x)>0;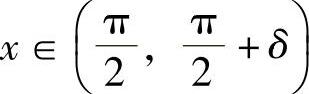 时,f′(x)<0,所以
时,f′(x)<0,所以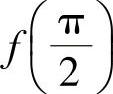 是f(x)的极大值.上述的δ是充分小的正数.
是f(x)的极大值.上述的δ是充分小的正数.
(11)分析 想法排除其中三个不正确选项即可.
精解 令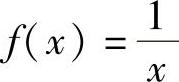 ,则f(x)与
,则f(x)与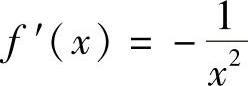 都在(0,1)内连续,但f(x)在(0,1)内无界,所以排除选项(A)与(B).
都在(0,1)内连续,但f(x)在(0,1)内无界,所以排除选项(A)与(B).
选项(D)显然不正确,这是因为f(x)在(0,1)内有界未必可导,当然谈不上f′(x)在(0,1)内有界.
因此本题选(C).
附注 当函数f(x)在(a,b)内连续时,在(a,b)内未必有界.但本题表明:
当f′(x)在(a,b)内有界时,f(x)必在(a,b)内有界.证明如下:
对任意x∈(a,b),有
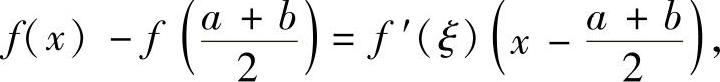
于是有
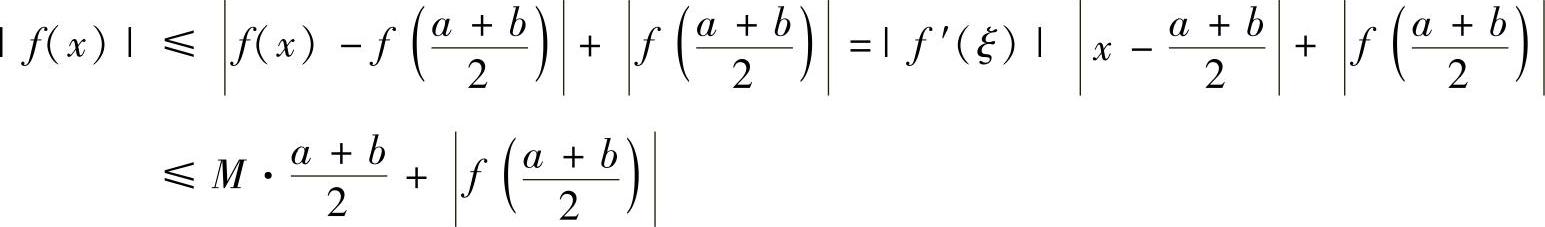
(由于f′(x)在(a,b)内有界,故存在M>0,使得|f′(x)|≤M(x∈(a,b))),即f(x)在(a,b)内有界.
(12)分析 从公式AA∗=|A|E(E为三阶单位矩阵)入手选择正确选项.
精解 由AA∗=|A|E及题设A∗=AT得
AAT=|A|E,(1)
即
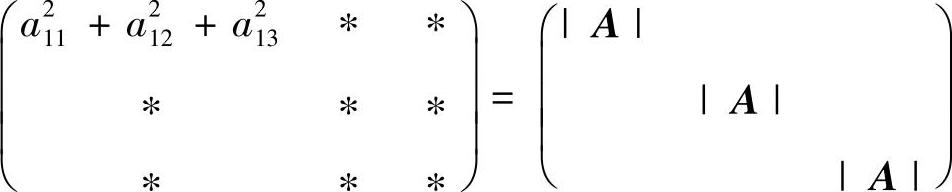 (∗表示不必计算出来的元素),由此可知,
(∗表示不必计算出来的元素),由此可知,
|A|=a211+a212+a213=3a211>0.(2)
另一方面,由式(1)得|AAT|=|A|3,即|A|2=|A|3.考虑到|A|>0得|A|=1.于是式(2)成为1=3a211,即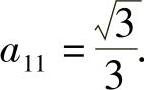
因此本题选(A).
附注 当线性代数的问题中出现n阶矩阵A的伴随矩阵A∗时,首先应想到以下公式
AA∗=A∗A=|A|E (其中E是n阶单位矩阵).
此外,应记住A∗的以下性质:
(ⅰ)|A∗|=|A|n-1(n≥2).
(ⅱ)A∗可逆的充分必要条件是A可逆,且A可逆时,A∗=|A|A-1,
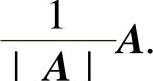
(ⅲ)A∗的秩为
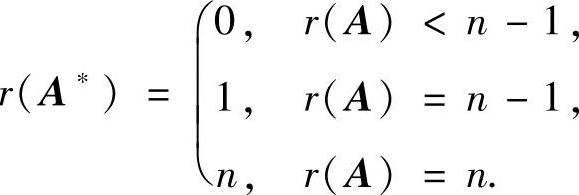
(ⅳ)设ξ是A的对应非零特征值λ的特征向量,则A∗有特征值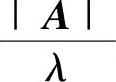 及对应的特征向量ξ.
及对应的特征向量ξ.
(13)分析 用线性无关向量组α1,α2表示向量组α1,A(α1+α2)即可得到后者线性无关的充分必要条件.
精解 由于α1,α2是A的对应不同特征值的特征向量,所以线性无关,于是由
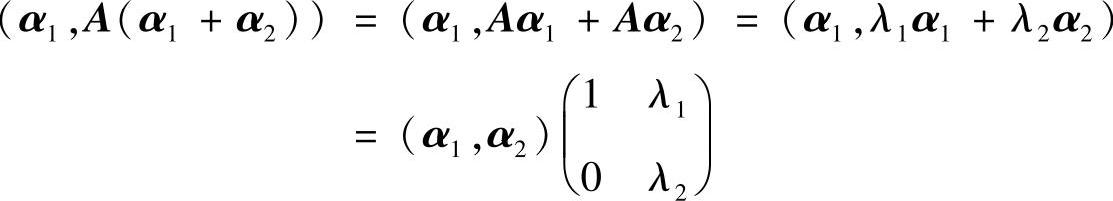
知α1,A(α1+α2)线性无关的充分必要条件是
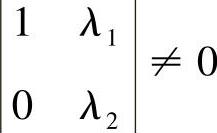 ,即λ2≠0.
,即λ2≠0.
因此本题选(D).
附注 记住以下结论:
设α1,α2,…,αn是一个n维列向量组,则该向量组线性无关的充分必要条件是|A|≠0(其中A=(α1,α2,…,αn)).
它的推广为:
α1,α2,…,αn是线性无关列向量组,且列向量组β1,β2,…,βn可由α1,α2,…,αn线性表示:
(β1,β2,…,βn)=(α1,α2,…,αn)A,则β1,β2,…,βn线性无关的充分必要条件为|A|≠0.
(14)分析 利用正态总体N(μ,σ2)在σ2未知时,μ的置信区间公式即可.
精解 当总体N(μ,σ2)在σ2未知时,μ的置信度为1-α=0.9(即α=0.1)的置信区间是
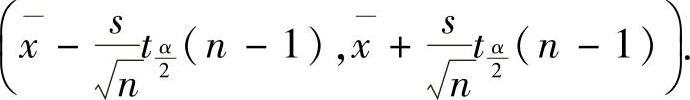
现将x=20,s=1,n=16,α=0.1代入得
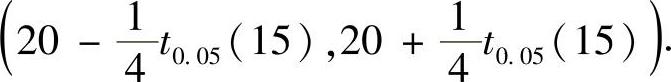
因此本题选(C).
附注 顺便指出,正态总体N(μ,σ2)在σ2已知时,μ的置信度为1-α的置信区间是
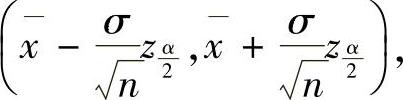
其中x是样本均值,n是样本容量,
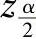 是标准正态分布N(0,1)的上侧
是标准正态分布N(0,1)的上侧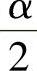 分位数.
分位数.
三、解答题
(15)分析 所给极限是∞-∞型未定式极限,通分转换成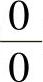 型未定式极限后再计算.
型未定式极限后再计算.
精解 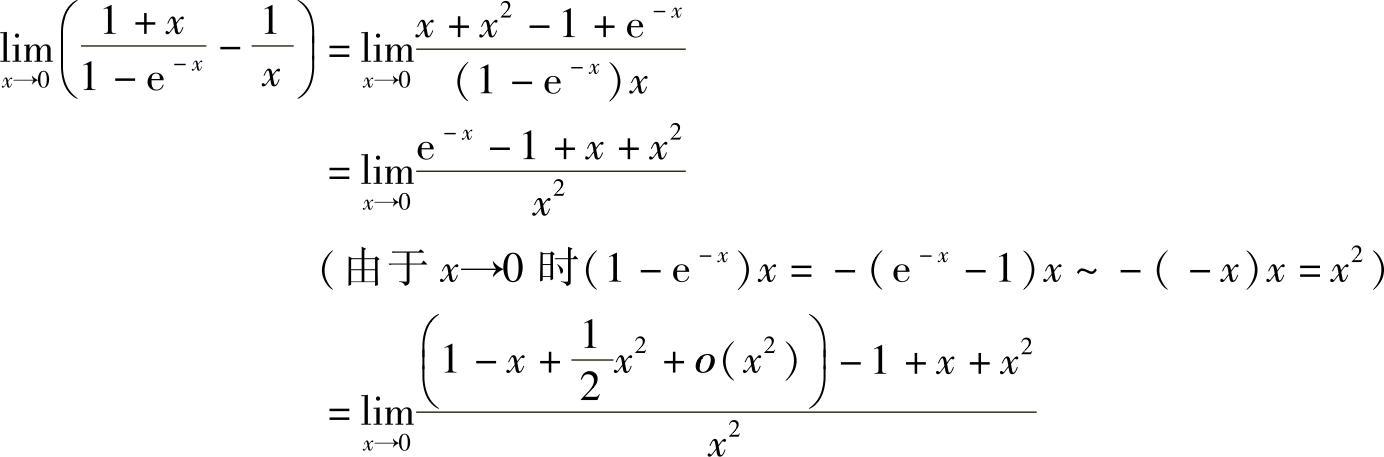

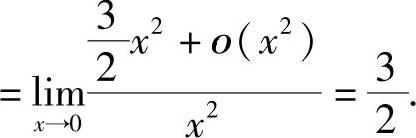
附注 本题也可用洛必达法则计算(当然首先需作些必要的化简):
 (https://www.daowen.com)
(https://www.daowen.com)
本题的有关计算方法见提高篇01.
(16)分析 利用复合函数求偏导数方法算出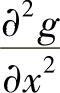 、
、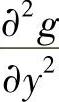 即可得问题的结果.
即可得问题的结果.
精解 由于
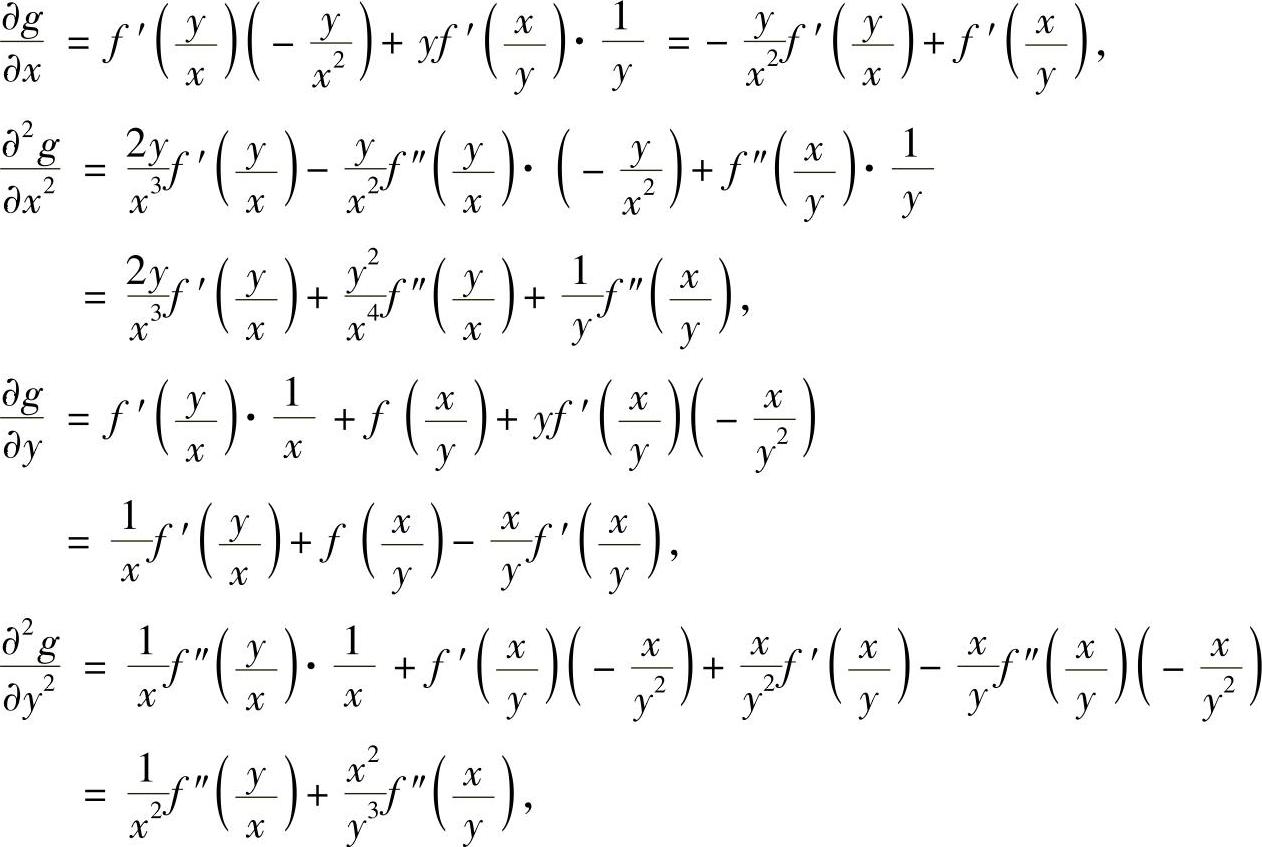
所以
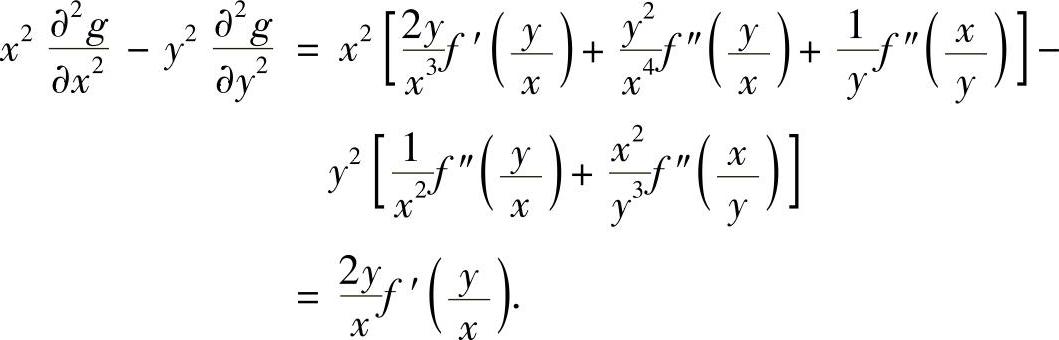
附注 要熟练掌握二元复合函数的一阶和二阶偏导数计算方法.
(17)分析 为了去掉被积函数中的绝对值号,用圆x2+y2=1将D分成D1与D2两部分,然后在各部分上分别计算二重积分后相加即可.
精解 用圆x2+y2=1将D分成D1与D2两部分(如图B.05.1所示),则
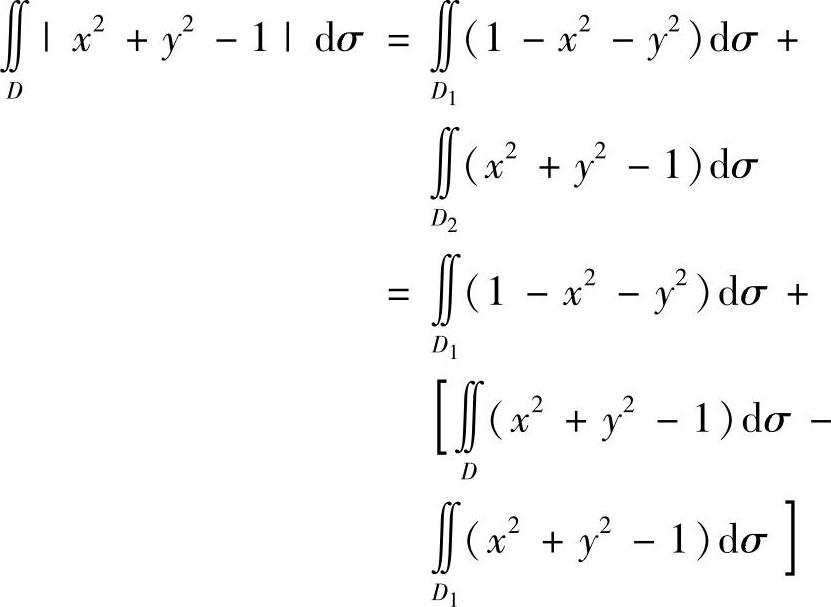
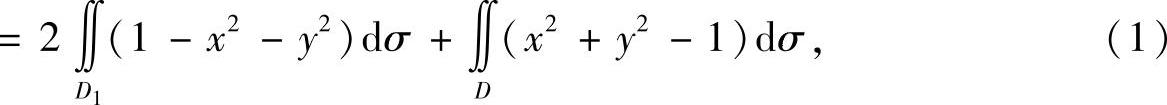
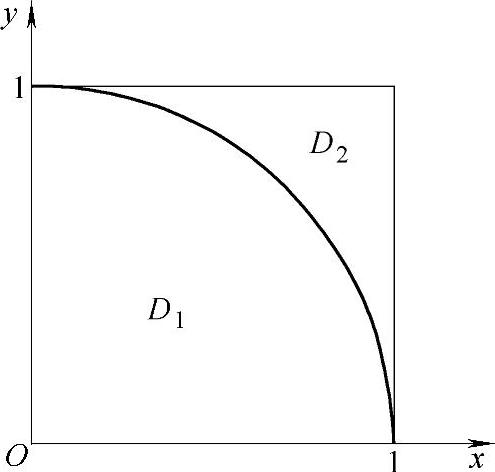
图 B.05.1
其中,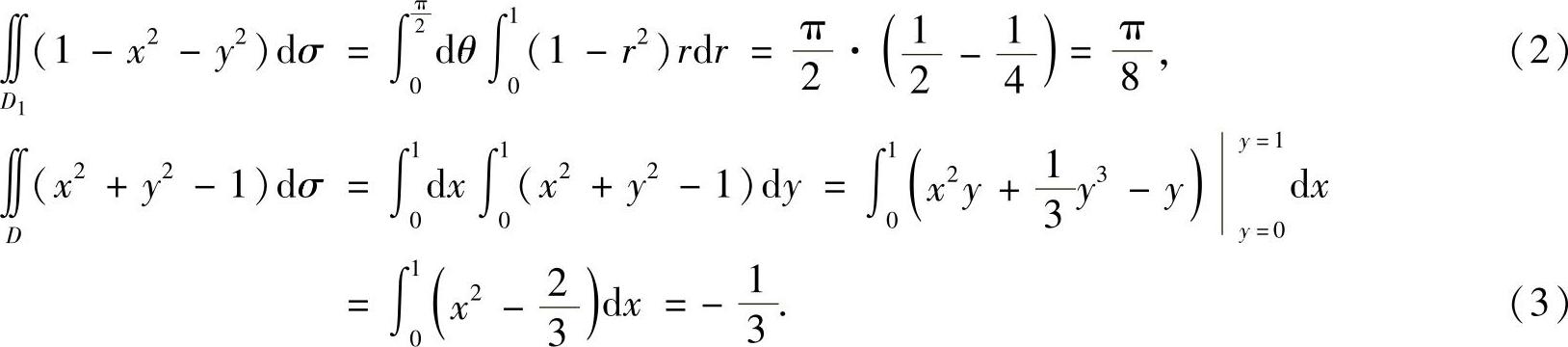
将式(2)、式(3)代入式(1)得
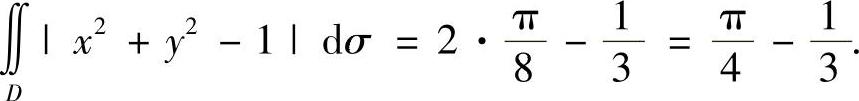
附注 (ⅰ)对于定积分,当被积函数中出现绝对值号时,总是适当划分积分区间,去掉绝对值号;
对于二重积分,当被积函数中出现绝对值号时,总是适当划分积分区域,去掉绝对值号.
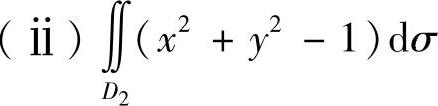 也可以如下运算:
也可以如下运算:
由于D2关于直线y=x对称,且x2+y2-1在对称点处的值彼此相等,所以

本题的有关内容及计算方法见提高篇12.
(18)分析 在(-1,1)内分别计算幂级数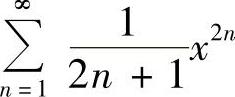 和
和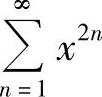 的和函数,然后相加即得s(x).
的和函数,然后相加即得s(x).
精解 在(-1,1)内,
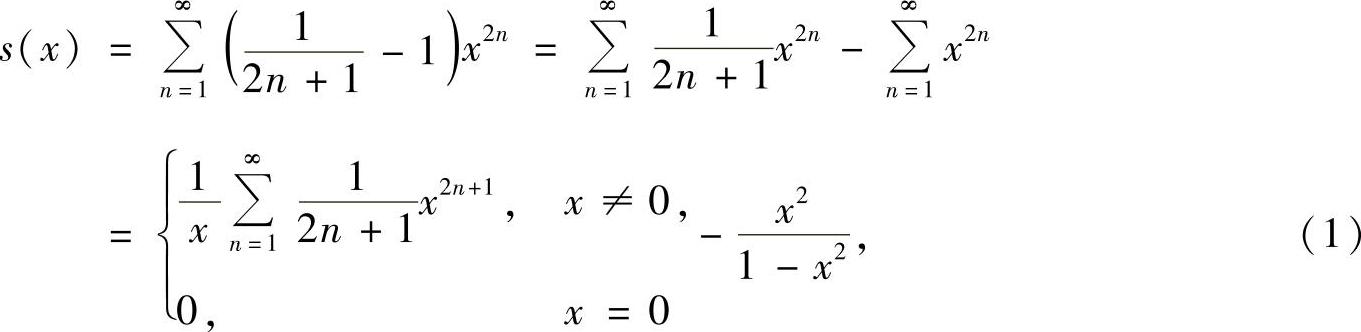
其中 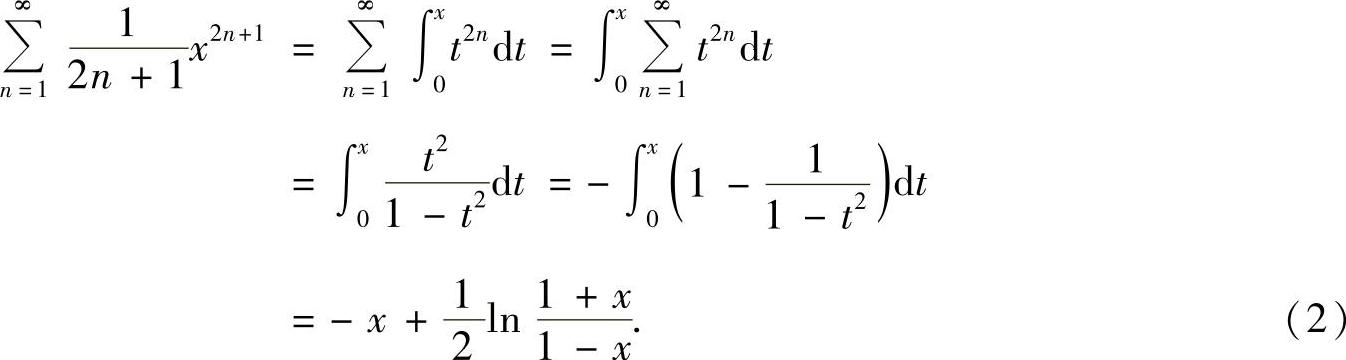
将式(2)代入式(1)得
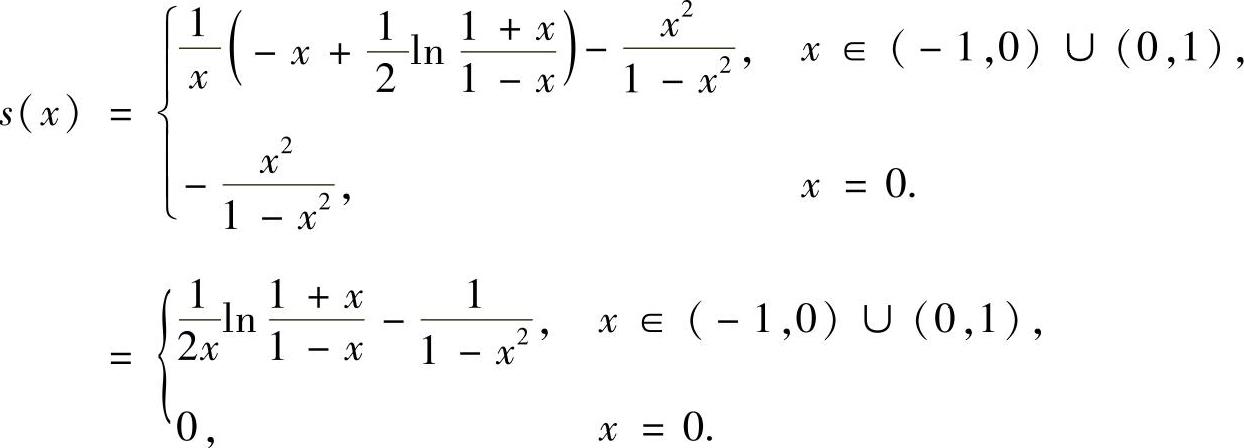
附注 在(-1,1)内,幂级数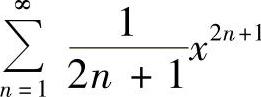 也可以按ln(1-x)的麦克劳林级数
也可以按ln(1-x)的麦克劳林级数
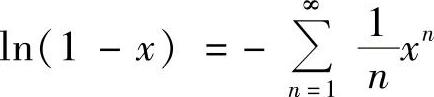
计算,具体如下:在(-1,1)内,
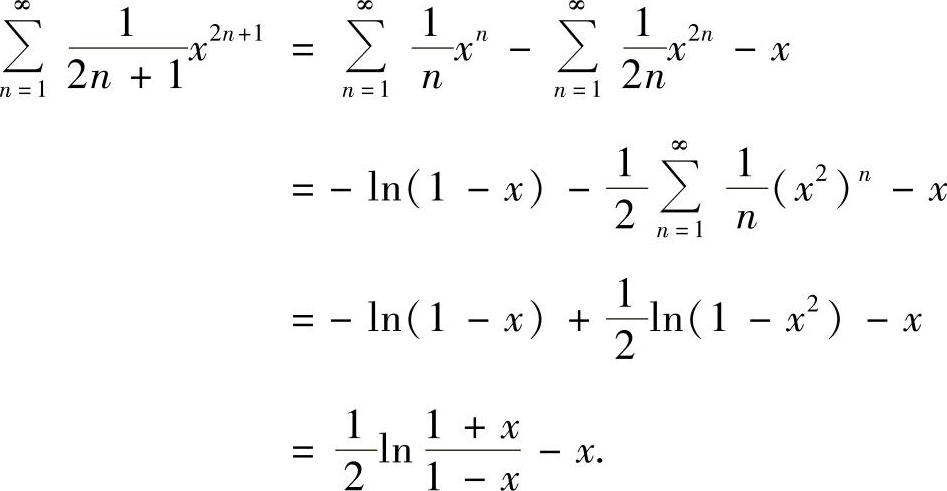
本题的有关计算方法见提高篇13.
(19)分析 将欲证不等式中的a改为x,且记
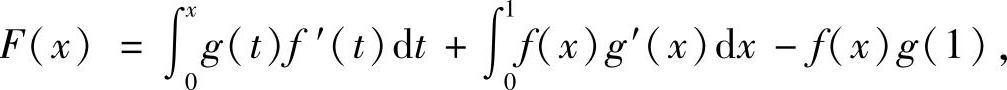
于是只要证明F′(x)≤0(x∈(0,1))即可.
精解 令
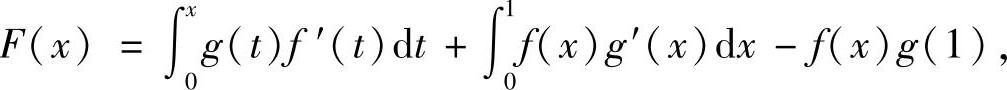
则F(x)在[0,1]上连续,在(0,1)内可导且由g′(x)≥0知g(x)-g(1)≤0,得
F′(x)=g(x)f′(x)-f′(x)g(1)=f′(x)[g(x)-g(1)]≤0,即F(x)在[0,1]上单调不增,从而对任何a∈[0,1]有
F(a)≥F(1),即
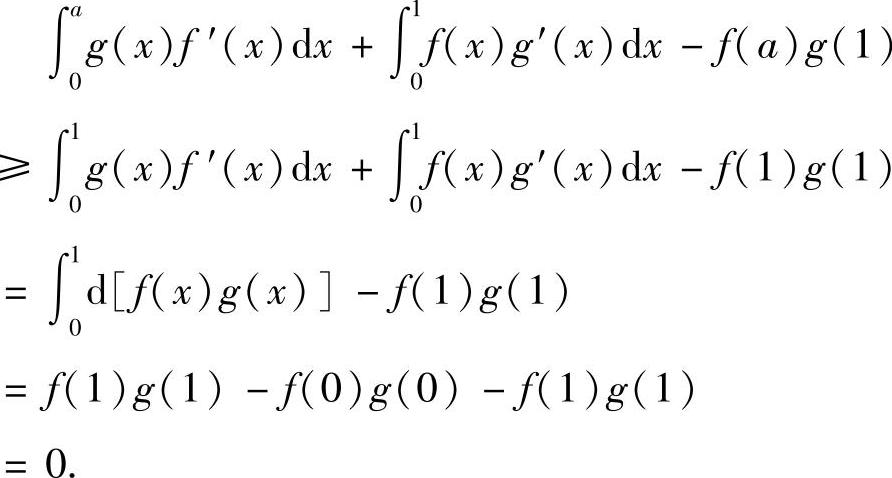
由此证得
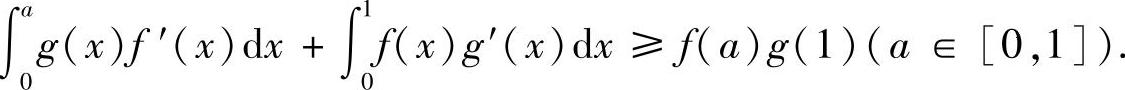
附注 本题也可以直接计算定积分得到结论:
对任意a∈[0,1]有
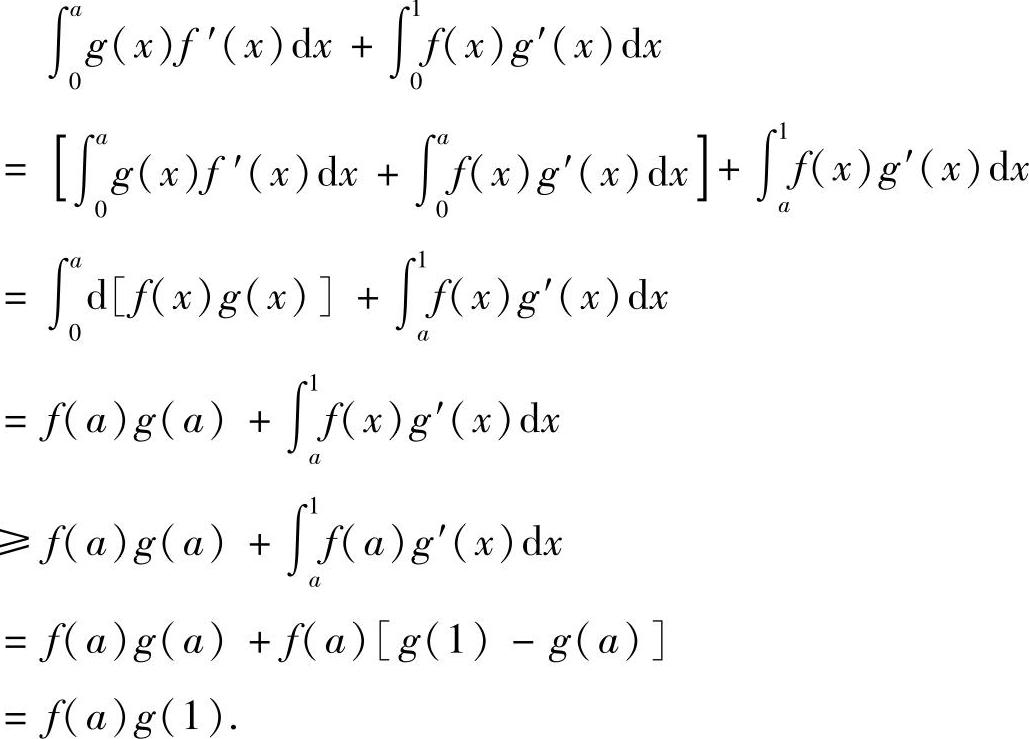
(20)分析 由于方程组(Ⅱ)有非零解,从而方程组(Ⅰ)与(Ⅱ)组成的方程组有非零解,由此可以算得a,b,c的值,并检验a,b,c取这些值时,(Ⅰ)与(Ⅱ)是否同解即可.
精解 由于方程组(Ⅱ)的系数矩阵秩≤2<3(未知数个数),所以有非零解,于是由方程组(Ⅰ)、(Ⅱ)同解知由(Ⅰ)、(Ⅱ)组成的方程组
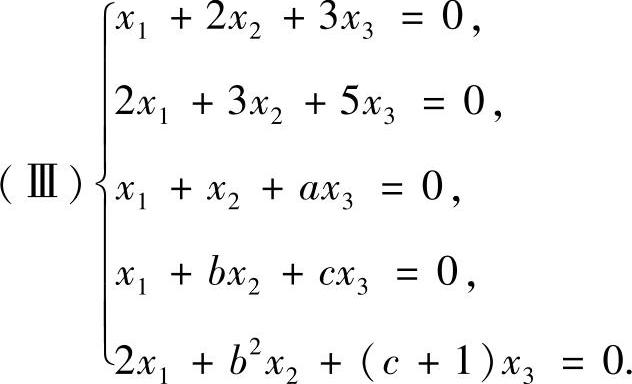
有非零解,从而它的系数矩阵A的秩r(A)<3.另一方面由(Ⅲ)可知,r(A)≥2.所以r(A)=2.
对A施行初等行变换:
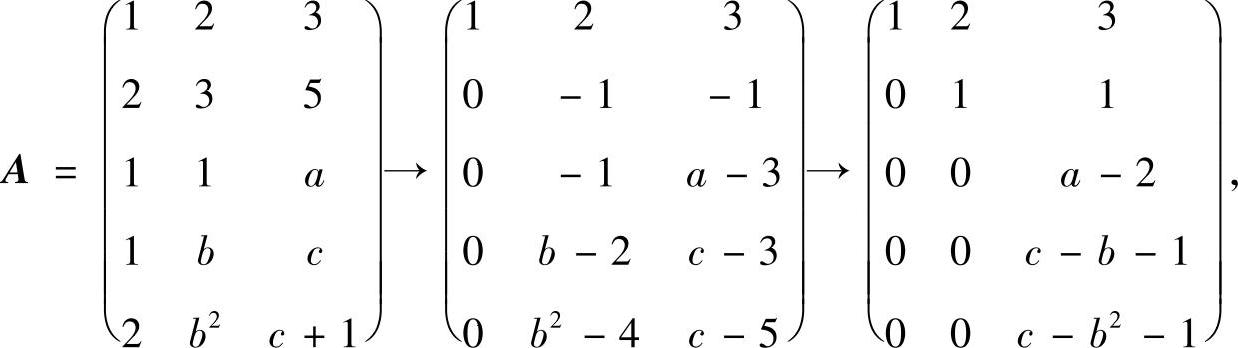
于是由r(A)=2得
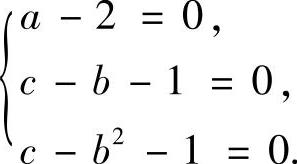 即a=2,b=1,c=2或a=2,b=0,c=1.
即a=2,b=1,c=2或a=2,b=0,c=1.
由于a=2,b=0,c=1时,方程组(Ⅰ)的秩为2,而方程组(Ⅱ)的秩为1,这与(Ⅰ)、
(Ⅱ)同解矛盾,所以a=2,b=1,c=2.
附注 本题也可按以下方法计算:
由于方程组(Ⅰ)的系数矩阵A1的秩为2,所以对A1施行初等行变换:

由此知a-2=0,即a=2,并且方程组(Ⅰ)与方程组
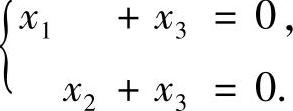
同解,从而(Ⅰ)的通解为k(-1,-1,1)T=(-k,-k,k)T(k是任意常数).(1)
由方程组(Ⅰ)与(Ⅱ)同解,式(1)也是方程组(Ⅱ)的解,即有
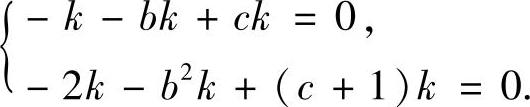
即
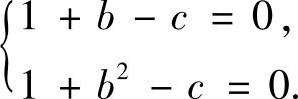
解此方程组得 b=0,c=1;b=1,c=2.
由于a=2,b=0,c=1不符合题意,所以a=2,b=1,c=2.
本题的有关内容和计算方法见提高篇18.
(21)分析 (Ⅰ)按分块矩阵乘法计算矩阵PTDP.
(Ⅱ)按正定矩阵的定义判定矩阵B-CTA-1C的正定性.
精解 (Ⅰ)由于AT=A,BT=B,所以由分块矩阵乘法得
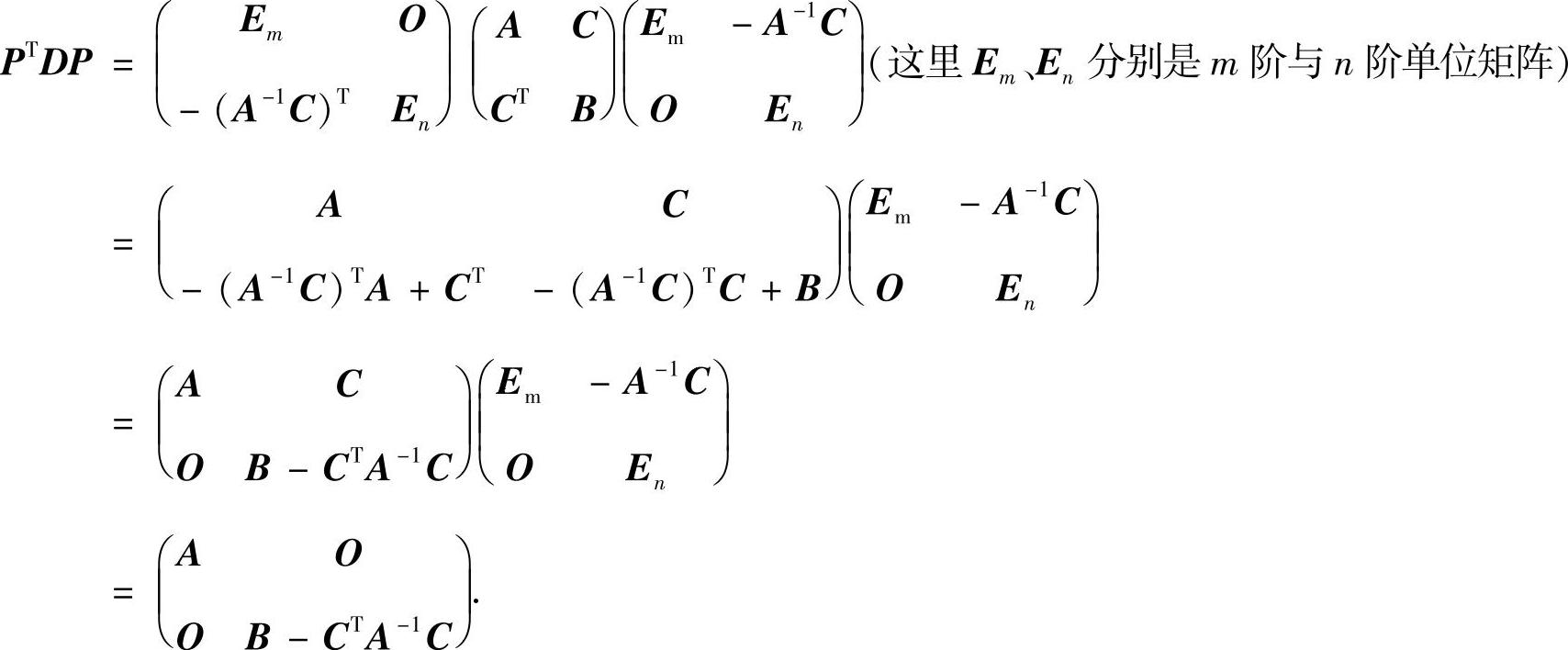
(Ⅱ)B-CTA-1C是正定矩阵.证明如下:
首先由A,B都是实对称矩阵得
(B-CTA-1C)T=BT-CT(A-1)TC=B-CT(AT)-1C=B-CTA-1C,因此,B-CTA-1C是实对称矩阵.
此外,对任意n维非零列向量x,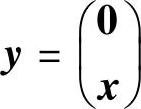 (其中0是m维零列向量)也是非零列向量.由P是可逆矩阵知Py也是非零列向量,因此由D是正定矩阵得
(其中0是m维零列向量)也是非零列向量.由P是可逆矩阵知Py也是非零列向量,因此由D是正定矩阵得
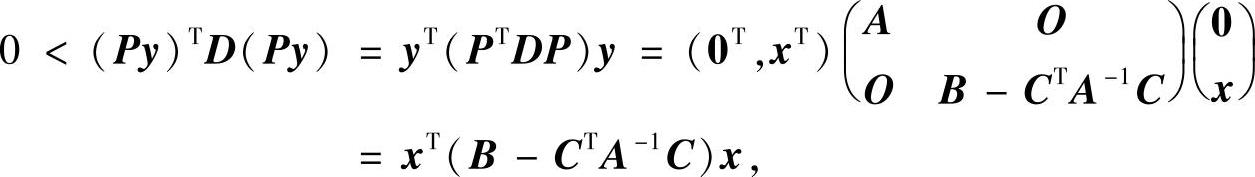
即对于任意n维非零列向量x有
xT(B-CTA-1C)x>0.
由此证得,B-CTA-1C是正定矩阵.
附注 以下(ⅰ)~(ⅴ)中的每一个都是n阶实对称矩阵A为正定矩阵的充分必要条件:
(ⅰ)以A为矩阵的二次型xTAx(其中x是n维列向量)为正定二次型;
(ⅱ)A的各阶顺序主子式都是正的;
(ⅲ)A与n阶单位矩阵(或正定矩阵)合同;
(ⅳ)A的特征值都为正的;
(ⅴ)存在n阶可逆矩阵C,使得A=CTC.
本题是综合题,有关内容与计算方法见提高篇17,20.
(22)分析 (Ⅰ)按边缘概率密度公式计算fX(x)和fY(y).
(Ⅱ)按公式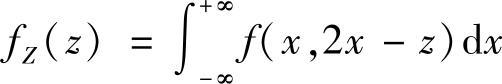 计算fZ(z).
计算fZ(z).
(Ⅲ)按条件概率计算公式计算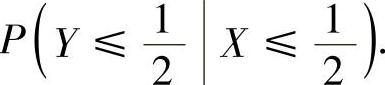
精解 (Ⅰ)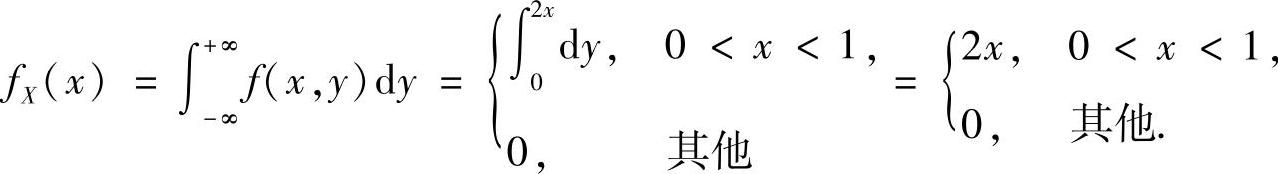
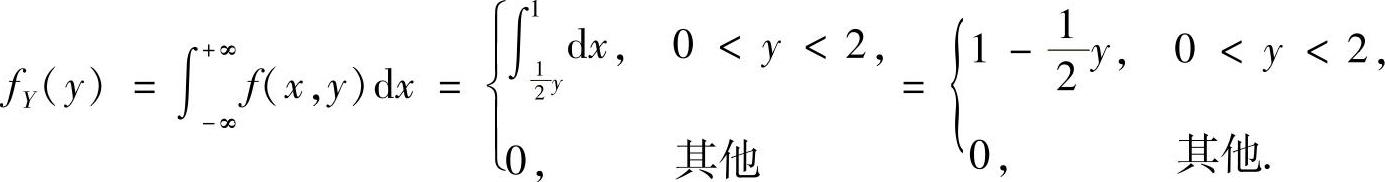
(Ⅱ)利用Z=2X-Y的概率密度计算公式得Z的概率密度为
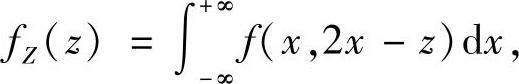
其中,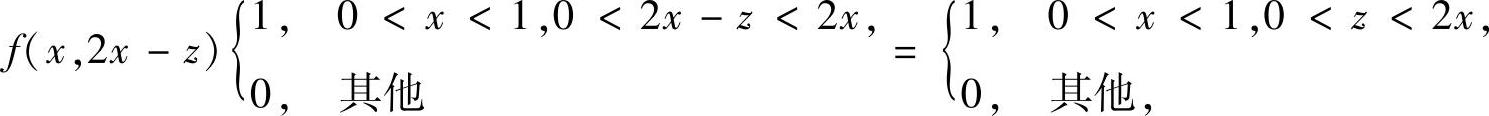
即f(x,2x-z)仅在图B.05.2a带阴影的△OAB内取值为1,xOz平面的其他部分取值为0,所以
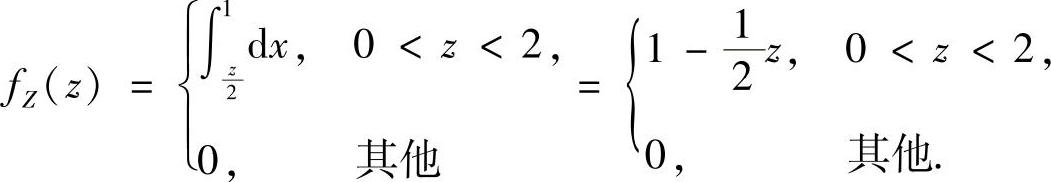
(Ⅲ)由条件概率计算公式得
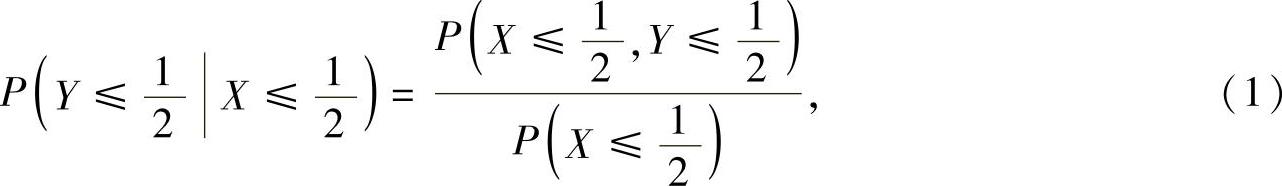
其中 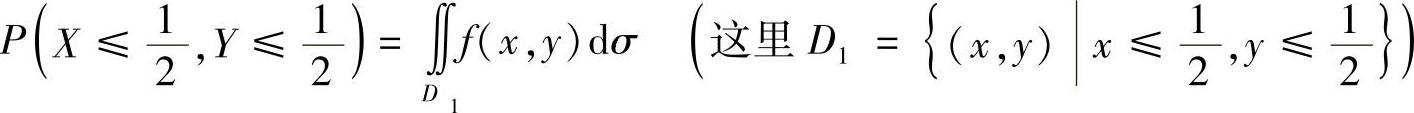

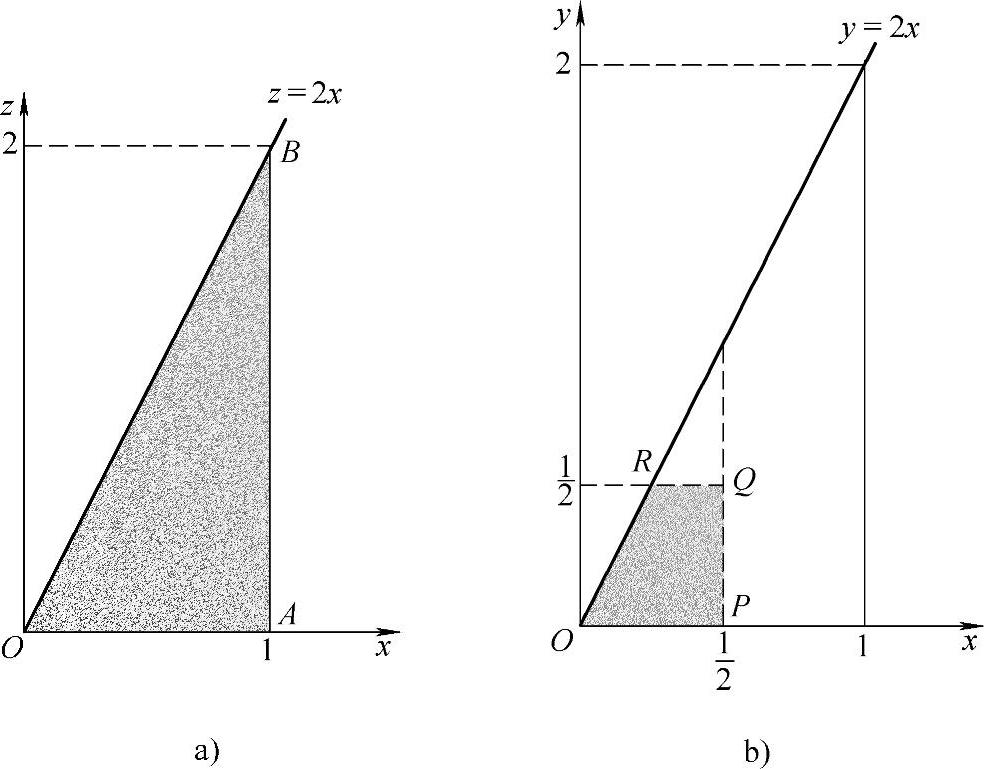
图 B.05.2
将式(2)、式(3)代入式(1)得
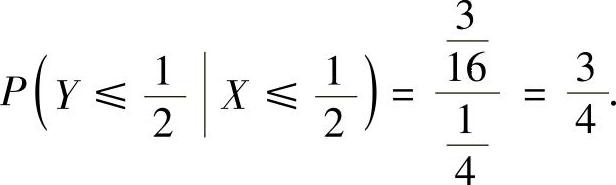
附注 记住以下公式将使有关计算变得快捷:
设二维随机变量(X,Y)的概率密度为f(x,y),则
当b≠0时,随机变量Z=aX+bY+c的概率密度可按公式
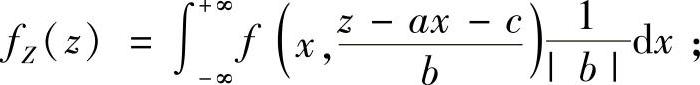
当a≠0时,随机变量Z=aX+bY+c的概率密度可按公式
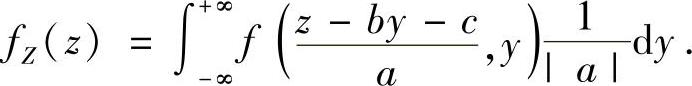
本题的有关内容及计算方法见提高篇23.
(23)分析 (Ⅰ)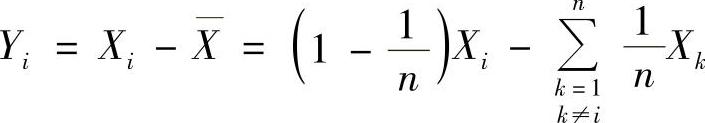 ,按此计算DYi.
,按此计算DYi.
(Ⅱ)由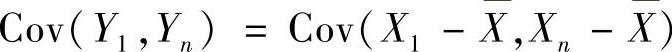 计算Cov(Y1,Yn).
计算Cov(Y1,Yn).
(Ⅲ)利用E[c(Y1+Yn)2]=σ2计算c的值.
精解 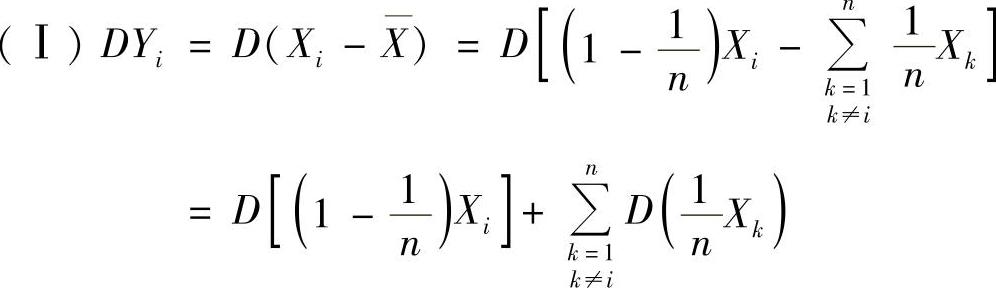
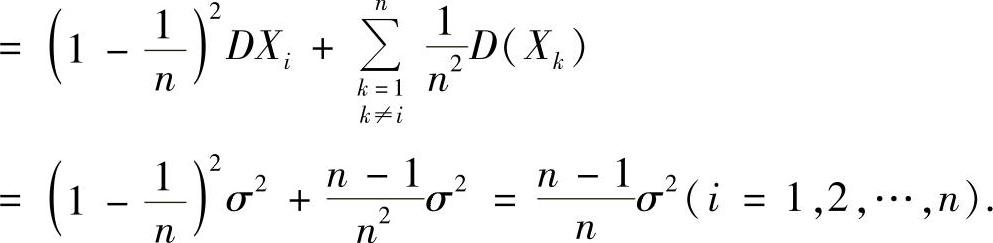
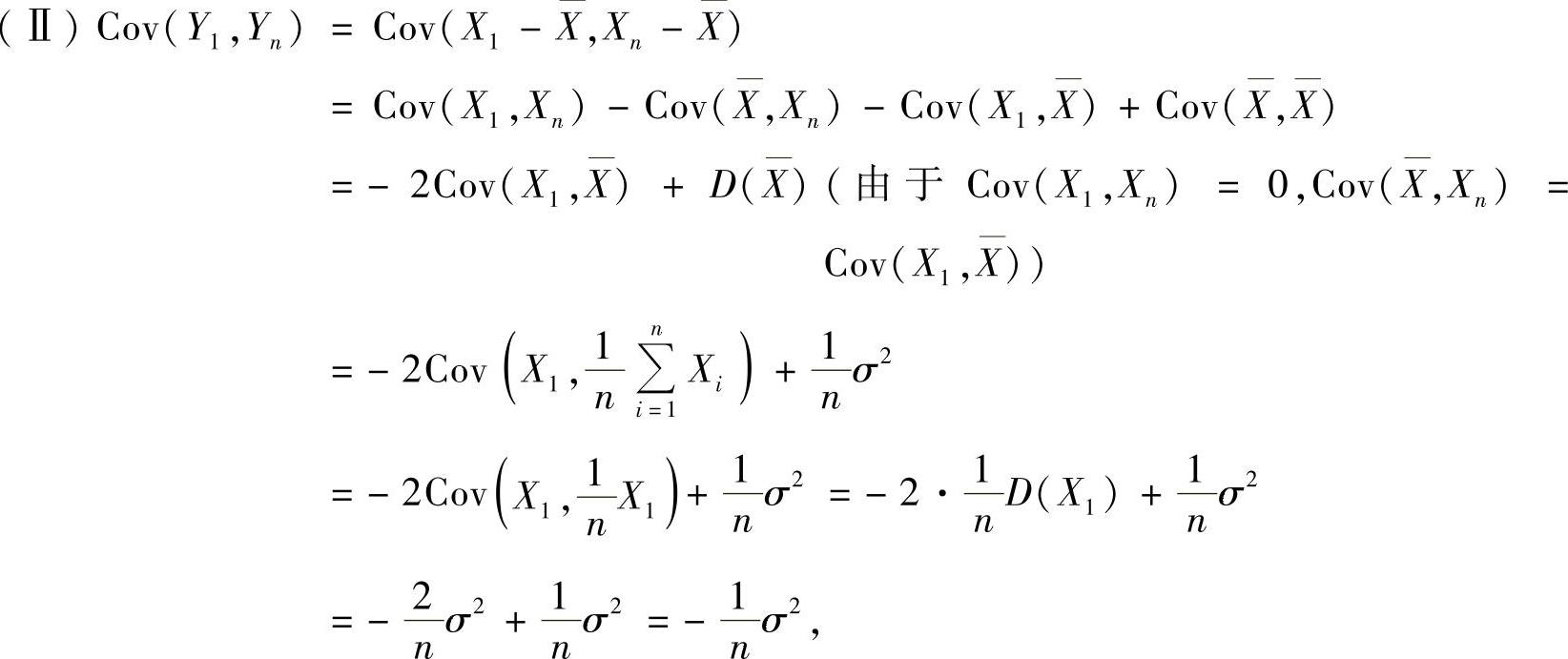
(Ⅲ)由题设有 E[c(Y1+Yn)2]=σ2,即
cE[(Y1+Yn)2]=σ2,(1)
其中 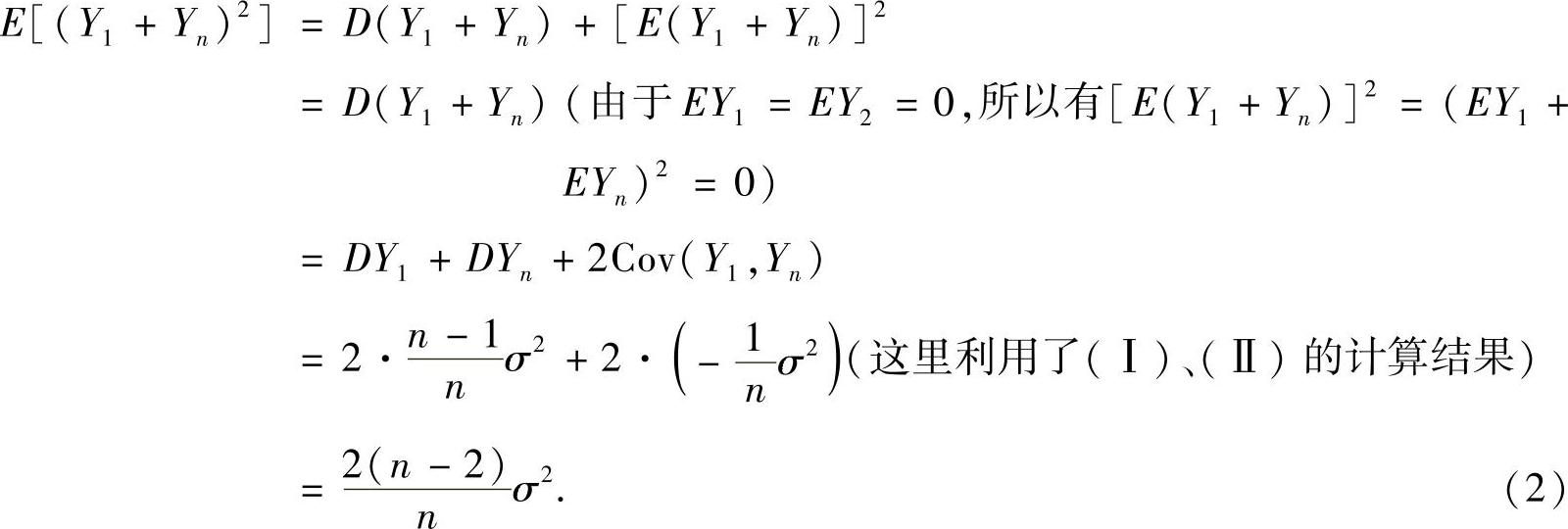
将式(2)代入式(1)得
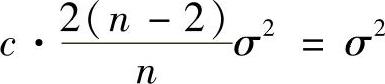 ,即
,即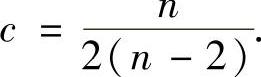
附注 应熟记随机变量的方差与协方差的性质:
(ⅰ)方差性质
设X,Y是随机变量,则
DC=0(C是常数),
D(CX)=D(CX+b)=C2DX(b,C都是常数),
D(X+Y)=DX+DY+2Cov(X,Y),特别当X与Y相互独立时,D(X+Y)=DX+DY,
DX=E(X2)-(EX)2.
(ⅱ)协方差性质
设X,Y,Z都是随机变量,则
Cov(X,Y)=Cov(Y,X),
Cov(aX,bY)=abCov(X,Y) (a,b是常数),
Cov(X+a,Y)=Cov(X,Y+b)=Cov(X,Y) (a,b是常数),
Cov(X,Y+Z)=Cov(X,Y)+Cov(X,Z),
Cov(X,Y)=E(XY)-EX·EY.
本题的有关内容及计算方法见提高篇24.
