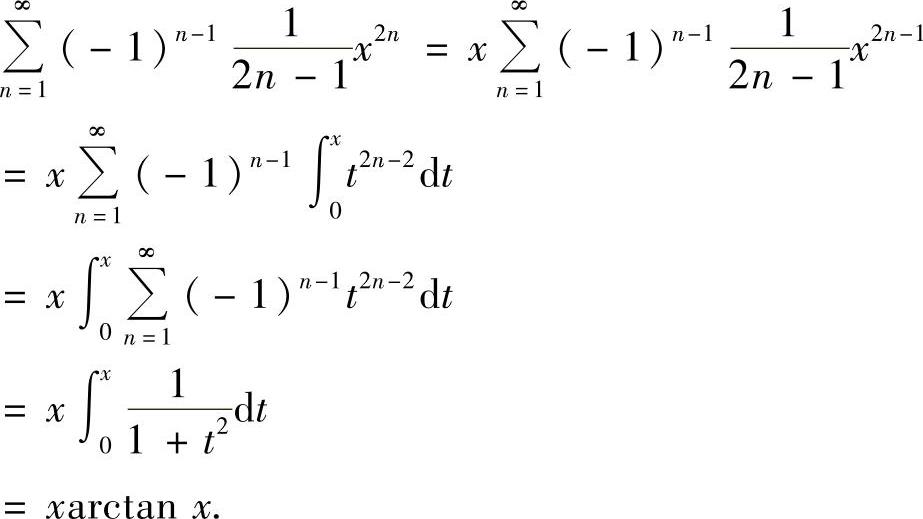6.2  幂级数的和函数的计算方法

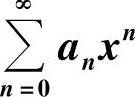6.2 幂级数 的和函数的计算方法

幂级数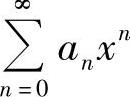的和函数可以按以下方法计算：

（1）对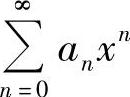进行适当的代数运算（例如，将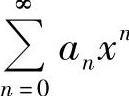的各项同乘以一个常数或x^k，或者提出一个常数或x^k，这里k为正整数），或作适当的变量代换，使其成为常用函数（指e^ax，sin ax，cos ax，ln（1+ax），（1+ax）^μ，这里a，μ都是常数）的麦克劳林级数，从而求得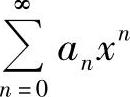的和函数.有时将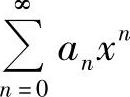表示成几个幂级数之和，然后对每个幂级数都作以上处理，由此算得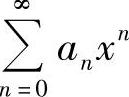的和函数.

（2）对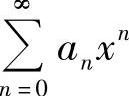在收敛区间内进行求导数或求二阶导数，或求积分，即

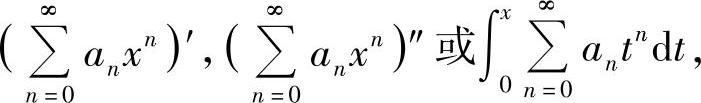
使其成为某个常用函数的麦克劳林级数，由此通过积分，二次积分或求导算得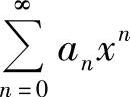的和函数.

例6.2 求幂级数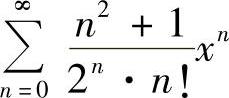的收敛域与和函数.

精解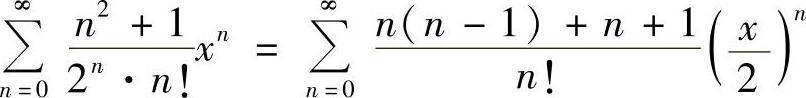

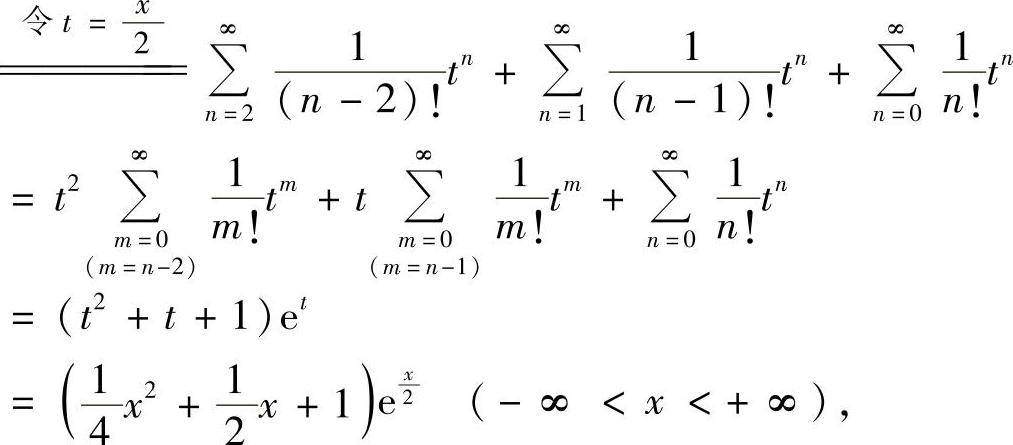
所以，所给幂级数的收敛域为（-∞，+∞），和函数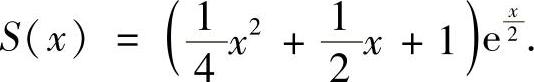

例6.3 求下列幂级数的收敛域与和函数：

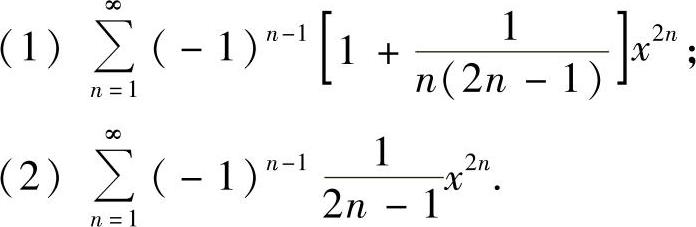
精解 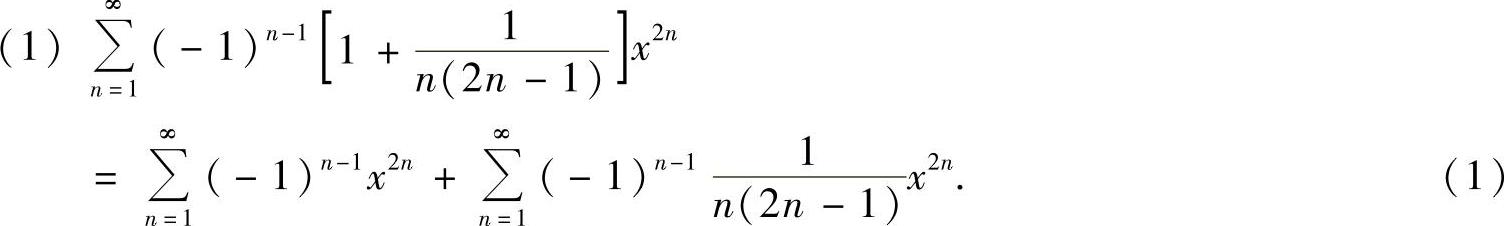显然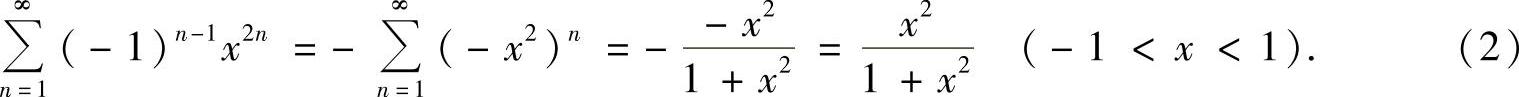，(https://www.daowen.com)

此外，对x∈（-1，1），记

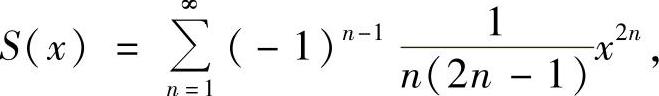
则

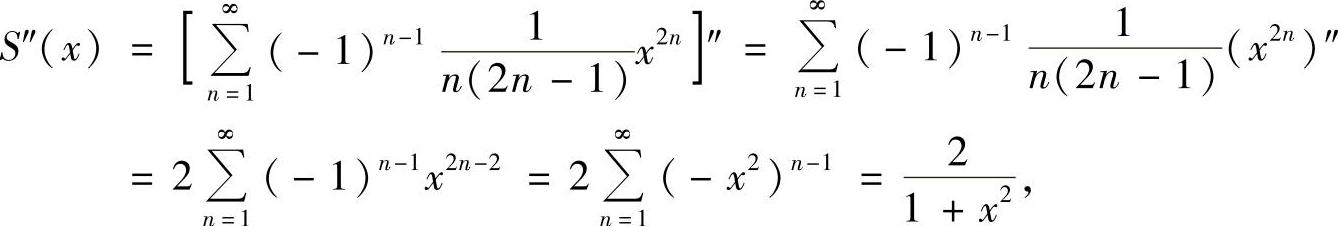
所以

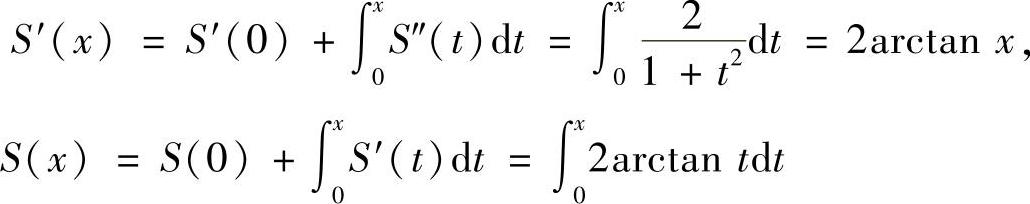
将式（2）、式（3）代入式（1）得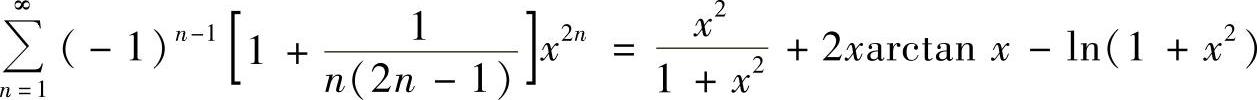 （-1<x<1）.

（2）记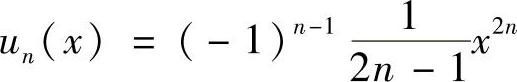，则

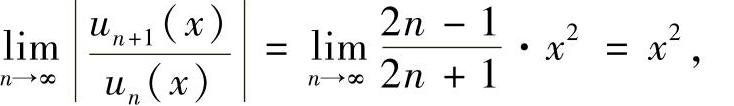
所以，所给幂级数的收敛区间为（-1，1）.由于x=-1，1时，所给幂级数都为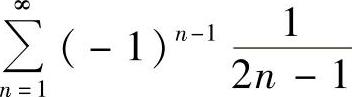，收敛.因此收敛域为[-1，1].

对x∈[-1，1]，有