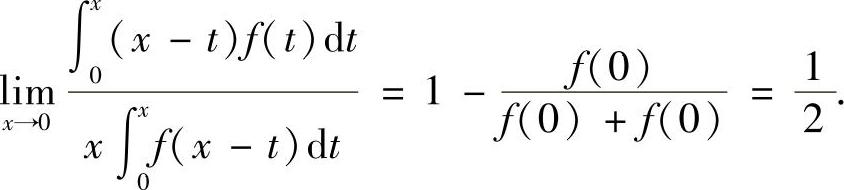1.1  型未定式极限的计算方法

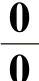1.1 型未定式极限的计算方法

设limf（x）=limg（x）=0，则称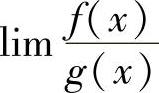为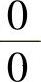型未定式极限，它可按以下步骤计算：

（1）化简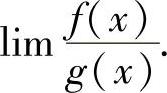常用的有以下五种方法：

a.消去f（x）与g（x）的公因子.

b.分子或分母有理化.

c.当x→x₀（x₀≠0）或x→∞时分别作变量代换t=x-x₀或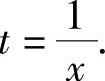

d.由极限运算法则算出其中非未定式部分的极限.

e.对f（x）与g（x）作等价无穷小代替，常用等价无穷小有：x→0时，sinx～x，tanx～x，arcsinx～x，arctanx～x，ln（1+x）～x，e^x-1～x，（1+x）μ-1～μx（μ≠0），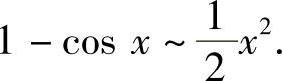

通过如上化简后，使得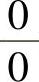型未定式极限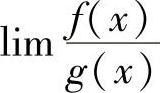变得十分简单，往往可以用极限运算法直接算出.

（2）如果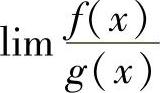不易作如上所述的化简，则可考虑使用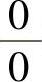型洛必达法则或对f（x）或g（x）应用麦克劳林公式，特别当f（x）或g（x）是积分上限函数时，必须首先应用洛必达法则，以消去积分运算.常用函数的麦克劳林公式是：x→0时，

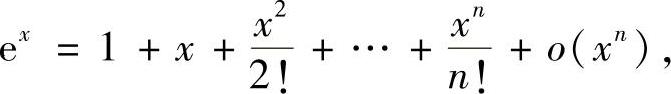
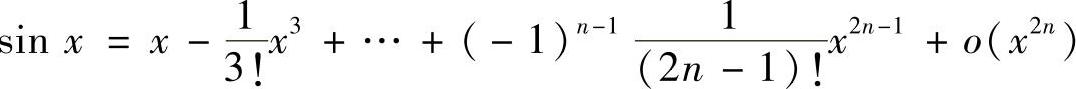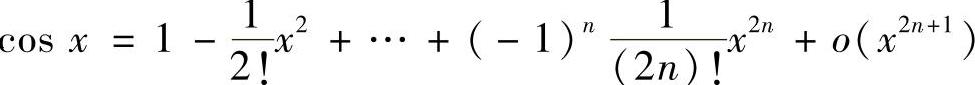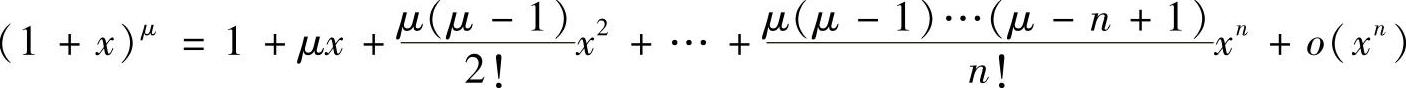，’，’特别地，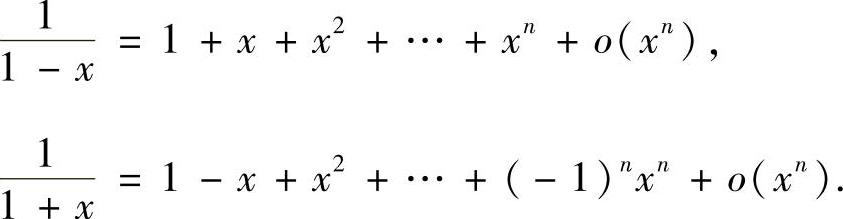

例1.1 计算下列极限：

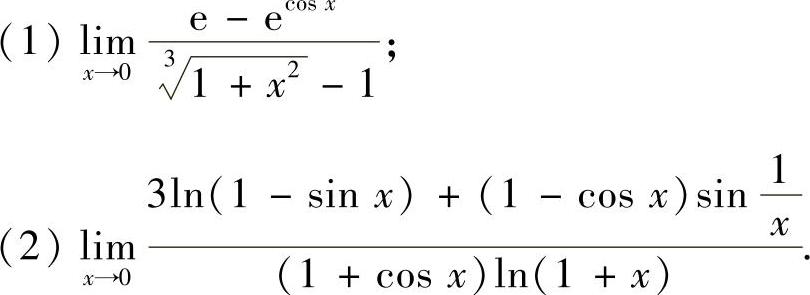
精解 （1）所给极限是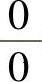型未定式极限.由于x→0时，

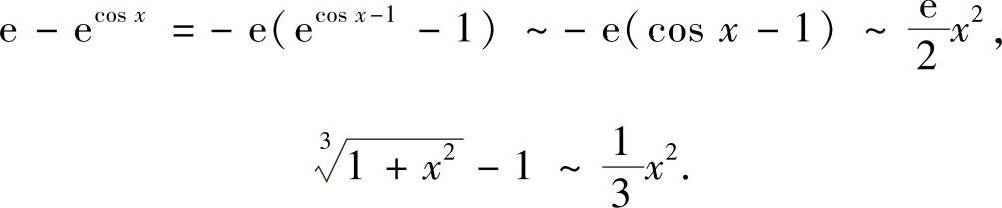
所以，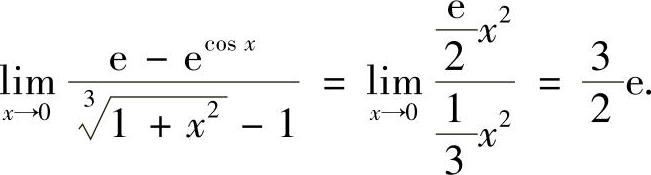

（2）所给极限是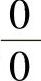型未定式极限.

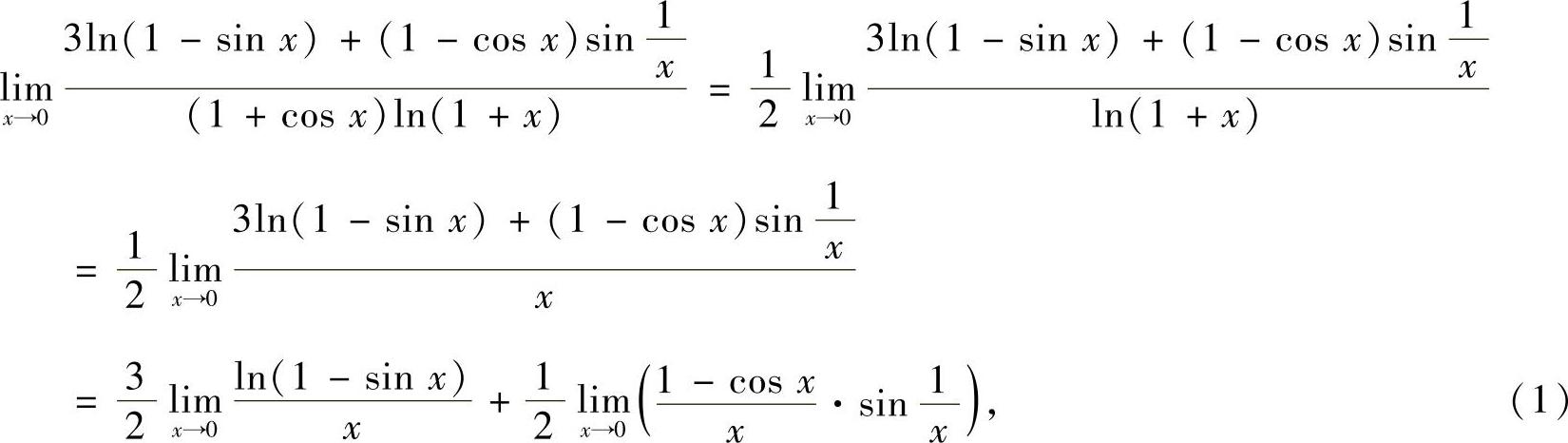
其中 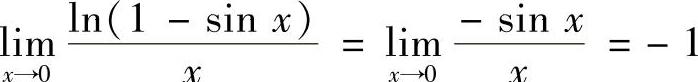’ 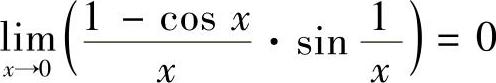（由于x→0时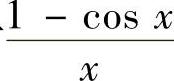是无穷小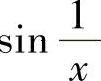，在点x=0的去心邻域内有界）.(https://www.daowen.com)

将它们代入式（1）得

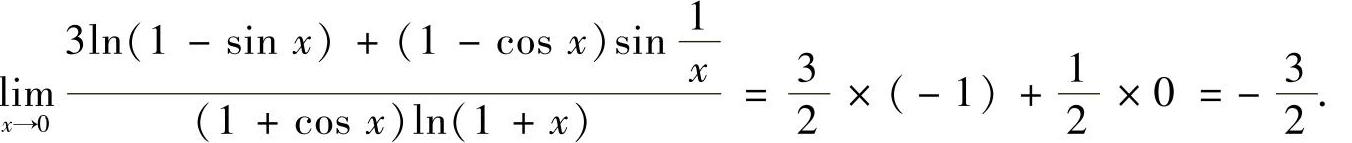
例1.2 求下列极限：

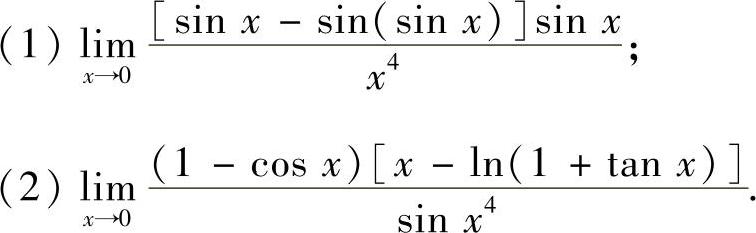
精解 （1）所给极限是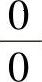型未定式极限.由于

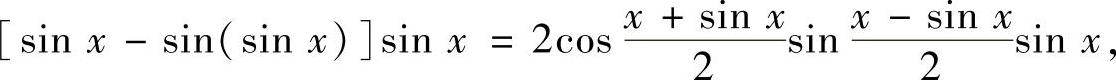
所以

（2）所给极限是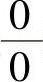型未定式极限.

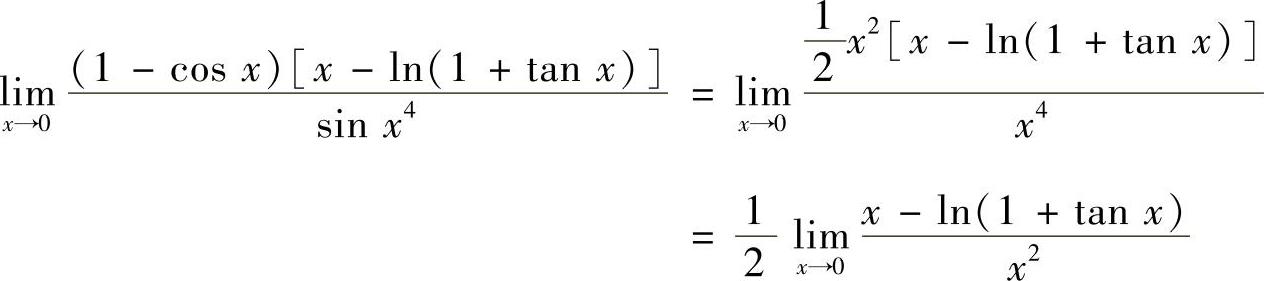
例1.3 计算下列极限.

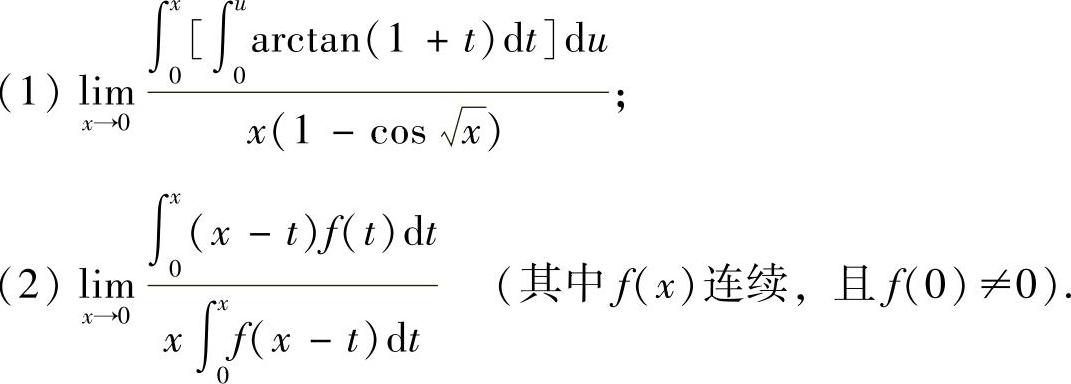
精解 （1）所给极限是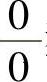型未定式极限.

（2）所给极限是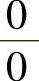型未定式极限.

其中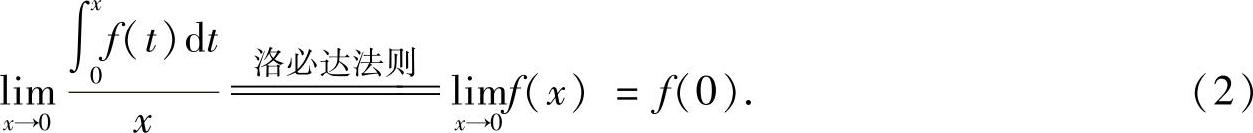

将式（2）代入式（1）得