6.1 幂级数收敛域的计算方法
2026年01月14日
6.1 幂级数
 收敛域的计算方法
收敛域的计算方法
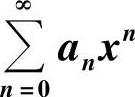 收敛域的计算方法
收敛域的计算方法
收敛域不为{0}的幂级数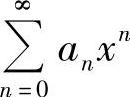 的收敛域可按以下步骤计算:
的收敛域可按以下步骤计算:
(1)用以下方法算出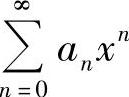 的收敛区间:如果
的收敛区间:如果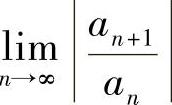 (或
(或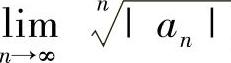 )存在为ρ,则当ρ≠0时,
)存在为ρ,则当ρ≠0时,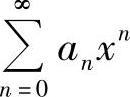 的收敛区间为
的收敛区间为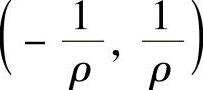 ;当ρ=0时,
;当ρ=0时,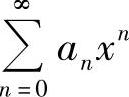 的收敛区间为(-∞,+∞).如果
的收敛区间为(-∞,+∞).如果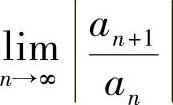 (或
(或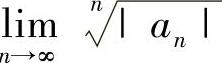 )不存在(例如
)不存在(例如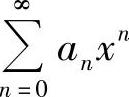 是缺项幂级数)时,将
是缺项幂级数)时,将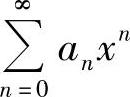 理解成
理解成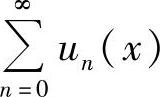 (其中对n=0,1,2,…,un(x)不恒为零),然后计算
(其中对n=0,1,2,…,un(x)不恒为零),然后计算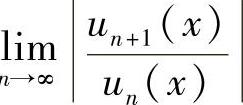 (或
(或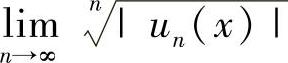 ),如果它们为ρ(x),则收敛区间为{xρ(x)<1}.
),如果它们为ρ(x),则收敛区间为{xρ(x)<1}.
(2)由收敛区间计算收敛域:
当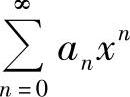 的收敛区间为(-∞,+∞)时,收敛域也为(-∞,+∞).
的收敛区间为(-∞,+∞)时,收敛域也为(-∞,+∞).
当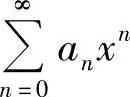 的收敛区间为(-R,R)(R>0)时,考虑
的收敛区间为(-R,R)(R>0)时,考虑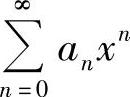 在点x=-R,R处的收敛性,将其中的收敛点并入收敛区间即得收敛域.
在点x=-R,R处的收敛性,将其中的收敛点并入收敛区间即得收敛域.
例6.1 求幂级数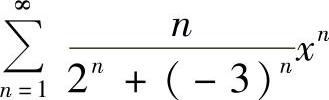 的收敛域.(https://www.daowen.com)
的收敛域.(https://www.daowen.com)
精解 记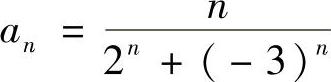 ,则
,则
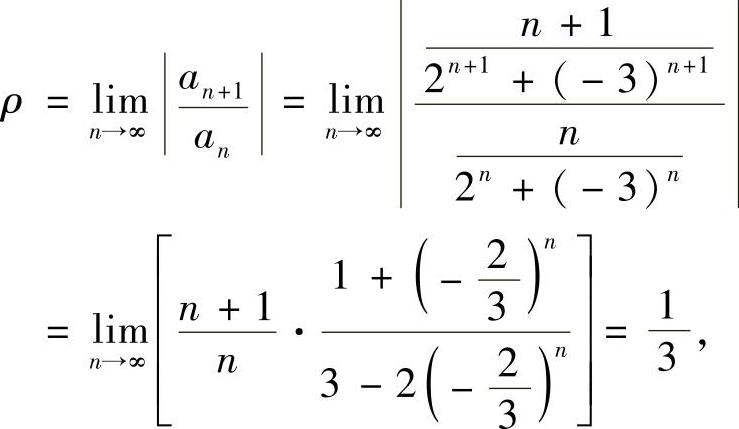
所以,所给幂级数的收敛区间为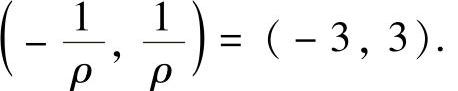
当x=-3,3时,所给幂级数分别为
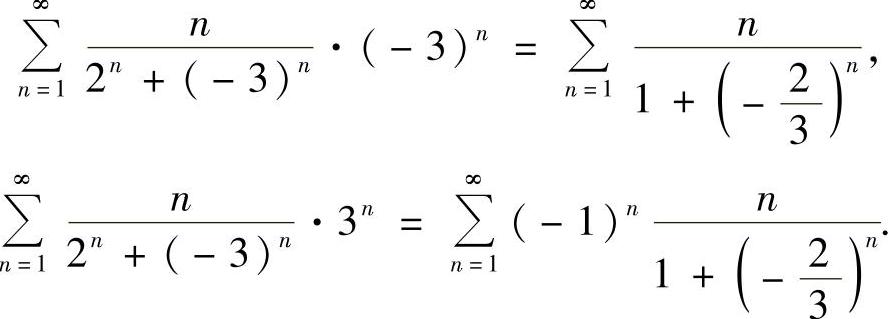
由于这两个级数的通项都不为零,所以发散.因此所给幂级数的收敛域为(-3,3).
