二重积分的计算

5.二重积分的计算

设f（x，y）是有界闭区域D上的连续函数，则二重积分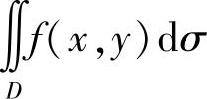可按以下步骤计算：

（1）画出D的简图，根据D的对称性，化简：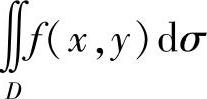

当D具有某种对称性时，如果f（x，y）在对称点处的值互为相反数，则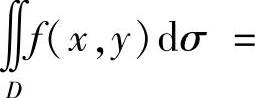；如果f（x，y）在对称点处的值彼此相等，则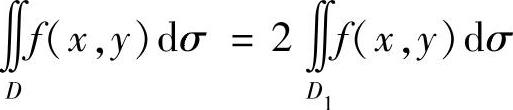（其中D₁是D按对称性划分成的两部分之一）.

记化简后的二重积分仍为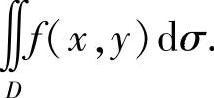

（2）根据D将二重积分转换成二次积分：

如果D={（x，y）|y₁（x）≤y≤y₂（x），a≤x≤b}（X型），则

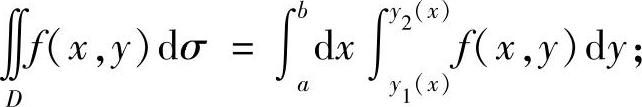
如果D={（x，y）|x₁（y）≤x≤x₂（y），c≤y≤d}（Y型），则

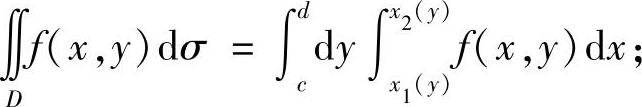
如果D是以原点为顶点的角域{（r，θ）|r₁（θ）≤r≤r₂（θ），0≤θ₁≤θ≤θ₂≤2π}，用极坐标计算，此时

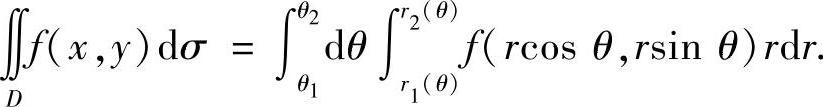
如果D不是上述三种形式的积分区域，则用若干条与y轴平行的直线（或与x轴平行的直线，或从原点出发的射线）将D划分成若干小块，使每一块为Y型（或X型，或角域），然后把每一小块上的二重积分化为二次积分.

（3）计算二次积分

例如，对于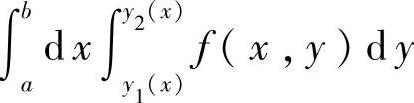，先将x看做[a，b]上的某个固定点计算定积分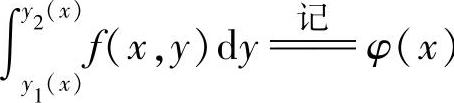，然后再计算定积分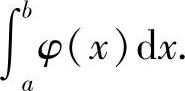

例5.1 计算下列二重积分：

（1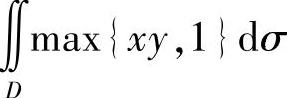），其中D={（x，y）0≤x≤2，0≤y≤2}；

（2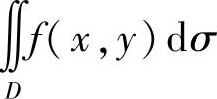），其中D={（x，y）|x|+|y|≤2，x≥0，y≥0}及

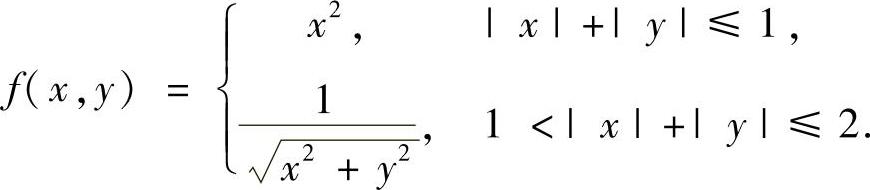
精解 （1）曲线xy=1将D分成D₁与D₂两部分（如图C.5.1所示），并且，在D上

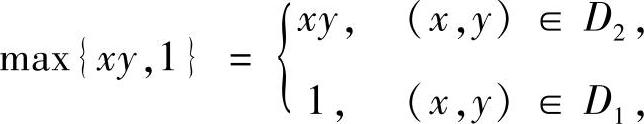
所以

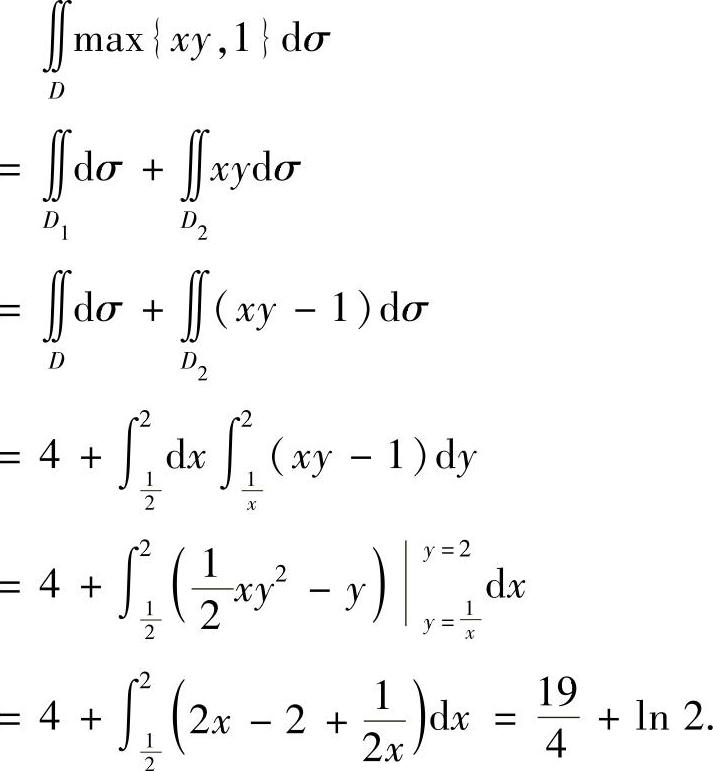
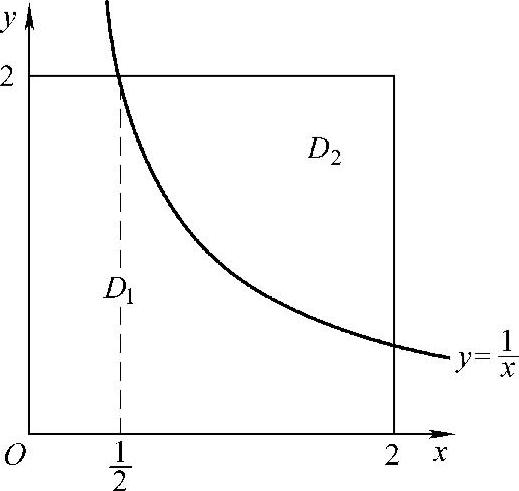
图 C.5.1

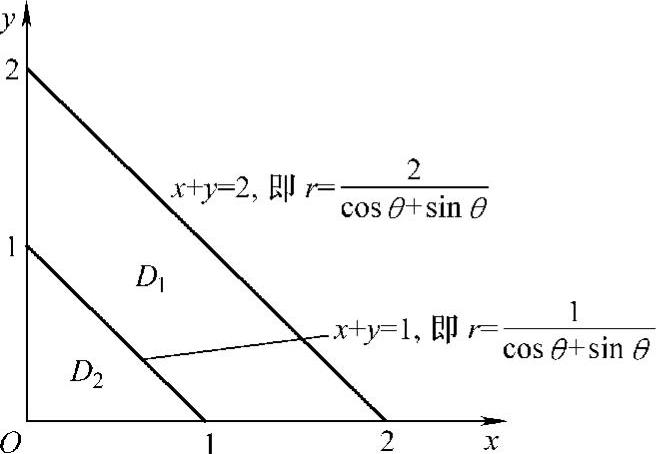
（2）用直线x+y=1将D划分成D₁与D₂两部分（如图C.5.2所示），则

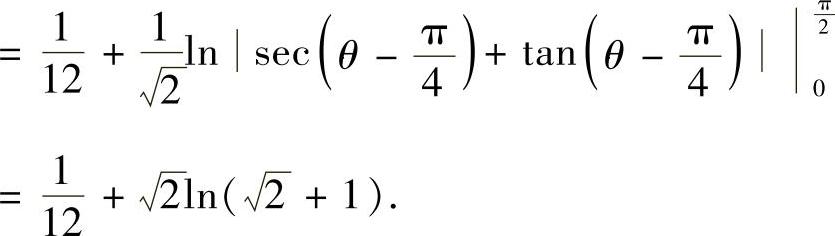
(https://www.daowen.com)

图 C.5.2

例5.2 计算下列二重积分：

（1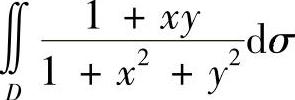），其中D={（x，y）x²+y²≤1，x≥0}；

（2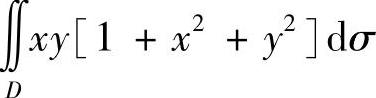），其中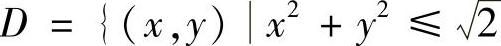，x>0，y>0}，[u]表示不超过u的最大整数；

（3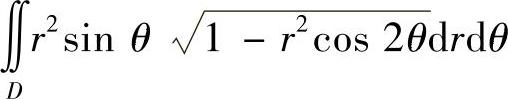），其中D={（r，θ）0≤r≤secθ，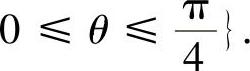

精解 （1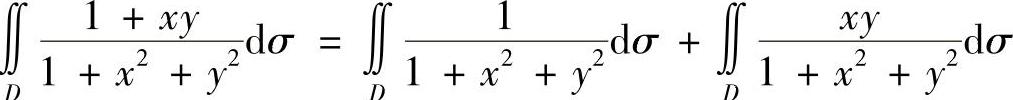），其中 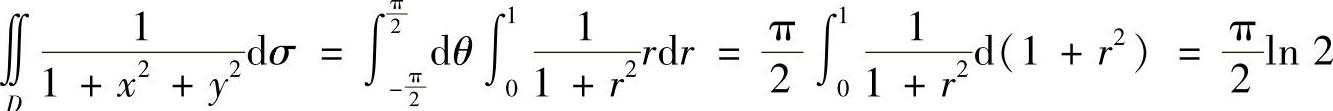’ 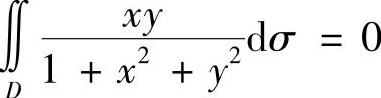（由于D关于x轴对称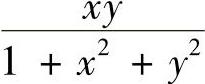，在对称点处的值互为相反数）.因此

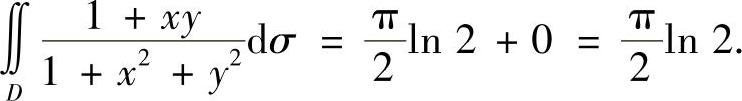
（2）用圆x²+y²=1将D划分成D₁={（x，y）|x²+y²<1，x>0，y>0}与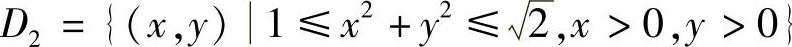，则在D上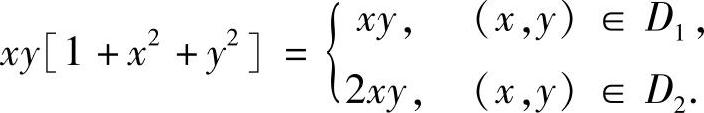，所以

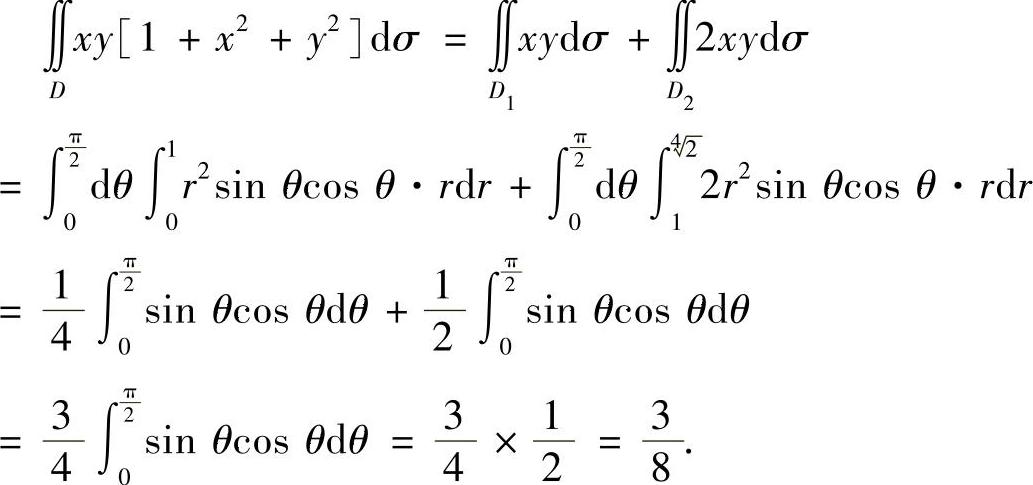
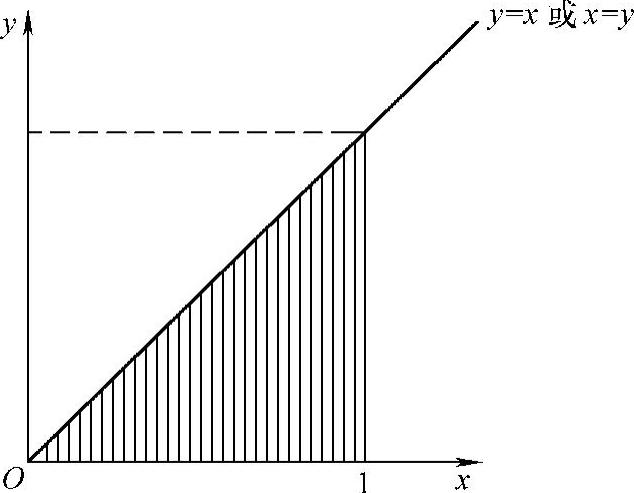
图 C.5.3

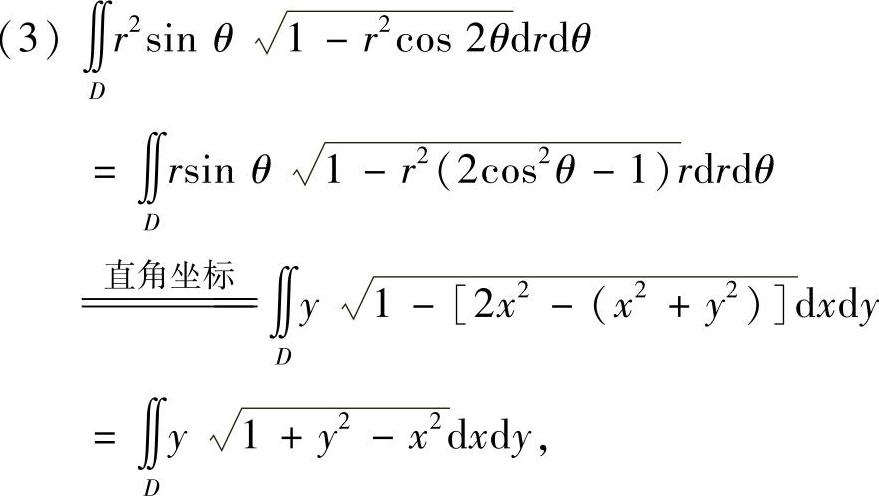
其中 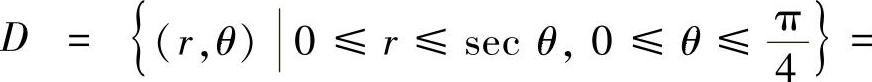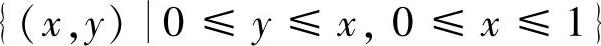（如图C.5.3阴影部分所示），所以

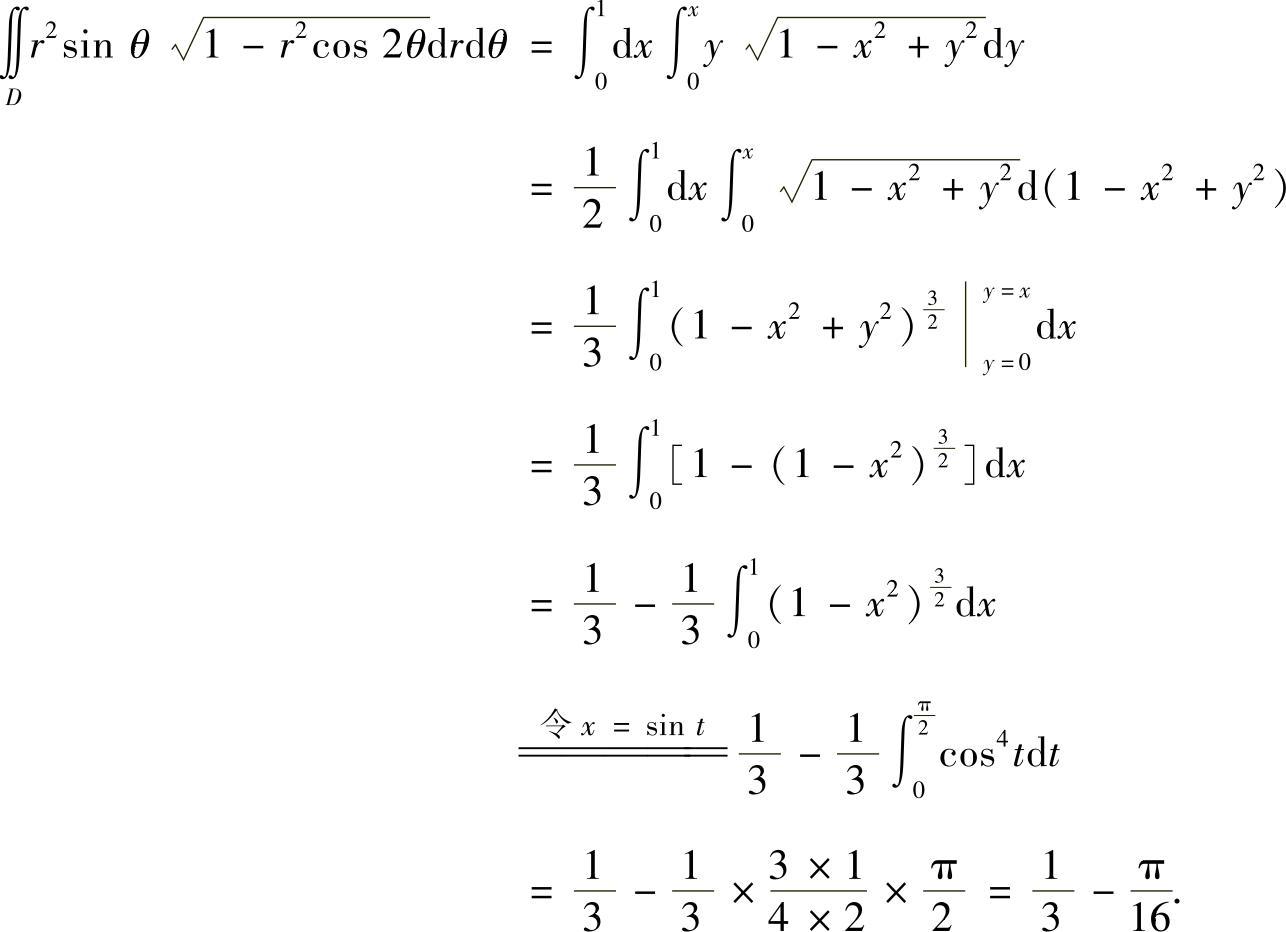
例5.3 计算下列二重积分：

（1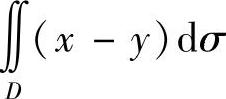），其中D={（x，y）|（x-1）²+（y-1）²≤2，y≥x}；

（2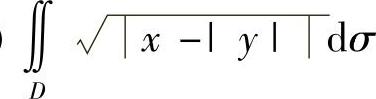），其中D={（x，y）|0≤x≤2，-1≤y≤1}.

精解 （1）D如图C.5.4阴影部分所示，它是角域的一部分，所以用极坐标计算所给的二重积分：

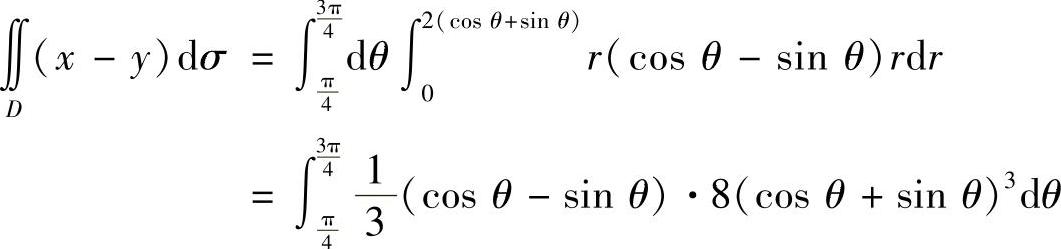
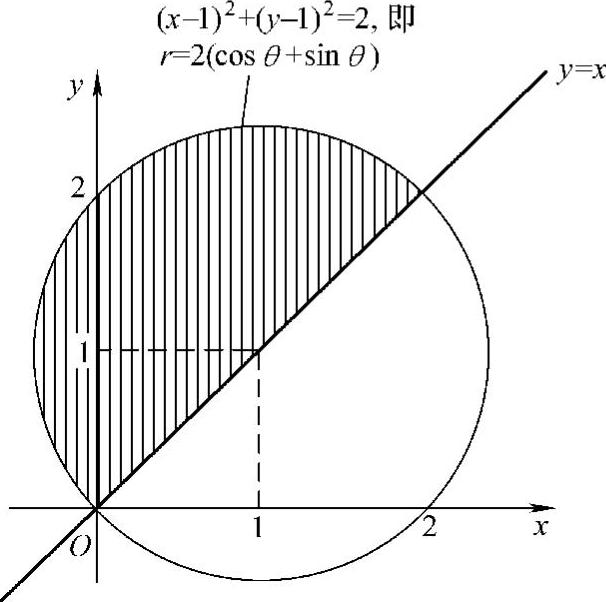
图 C.5.4

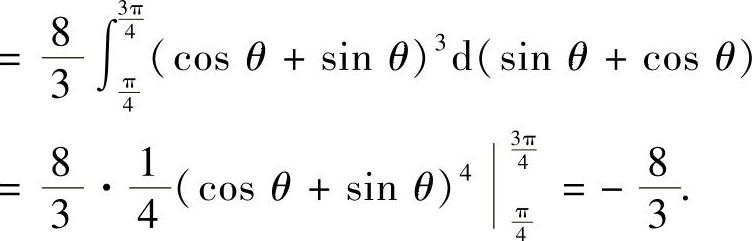
（2）由于D关于x轴对称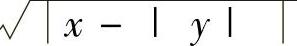，在对称点处的值彼此相等，所以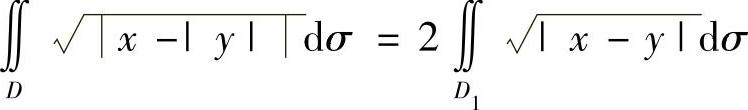，其中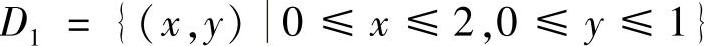是D的上半平面部分，如图C.5.5.用直线y=x将D₁划分成D₂与D₃两部分（其中D₂，D₃分别位于直线y=x的上方与下方），则

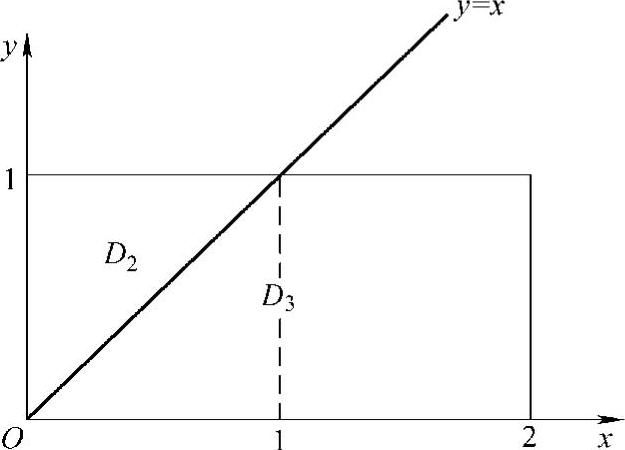
图 C.5.5