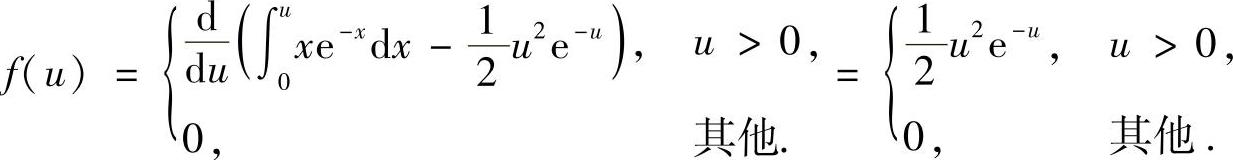13.2  二维连续型随机变量的各种概率密度的计算

13.2 二维连续型随机变量的各种概率密度的计算

设（X，Y）是二维连续型随机变量，f（x，y）与F（x，y）是它的概率密度与分布函数，则

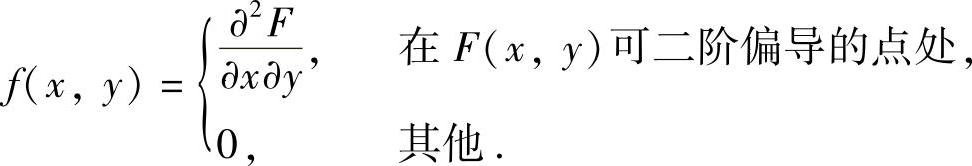
（X，Y）的边缘概率密度：

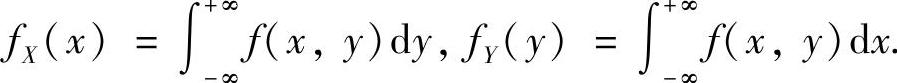
（X，Y）的条件概率密度：

对f_Y（y）≠0的任意y有，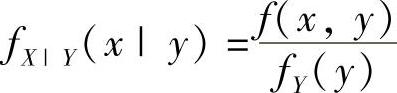

对f_X（x）≠0的任意x有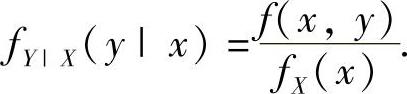

例13.1 设随机变量X的概率密度为

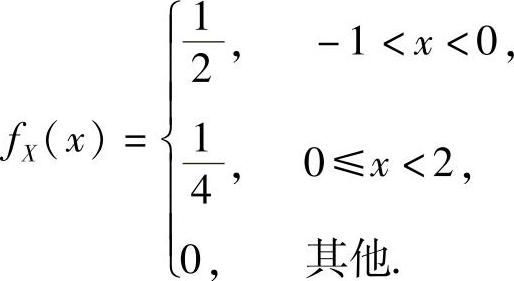
求Y=X²的概率密度.

精解 先计算Y的分布函数F_Y（y），然后求导算出Y的概率密度f_Y（y）.

按分布函数的定义F_Y（y）=P（Y≤y）=P（X²≤y）.

当y<0时，P（X²≤y）=P（∅）=0；

当y≥0时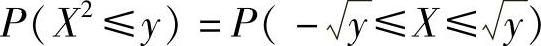，.于是

当0≤y<1时，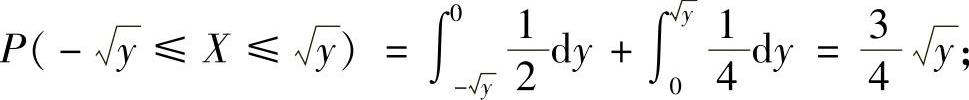

当1≤y<4时，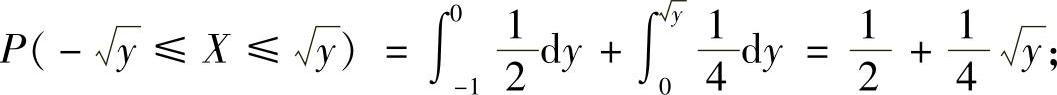

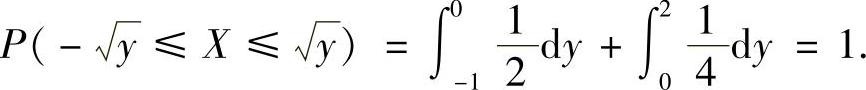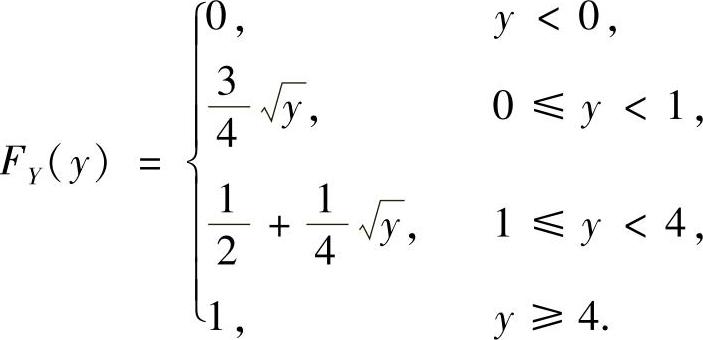当y≥4时，因此，从而

例13.2 设二维随机变量（X，Y）的概率密度为

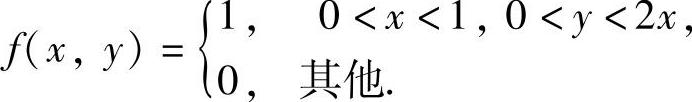
求：

（1）（X，Y）的边缘概率密度f_X（x），f_Y（y）；

（2）随机变量Z=2X-Y的概率密度f_Z（z）.

精解 （1）记D={（x，y）0<x<1，0<y<2x}（如图C.13.1阴影部分所示），则f（x，y）仅在D上取值为1，在xOy平面的其他部分取值为0.于是

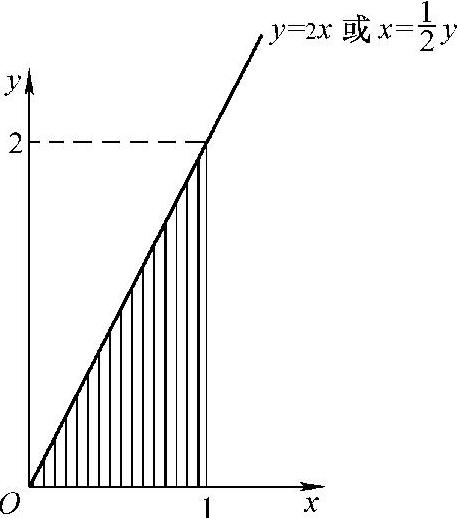
图 C.13.1

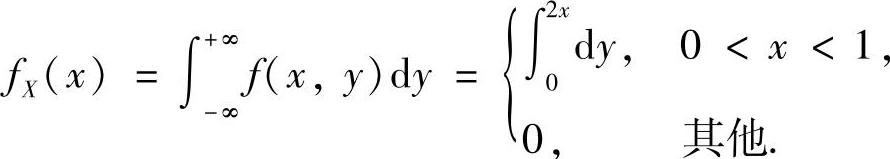
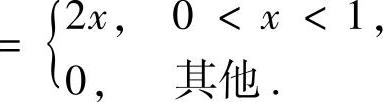
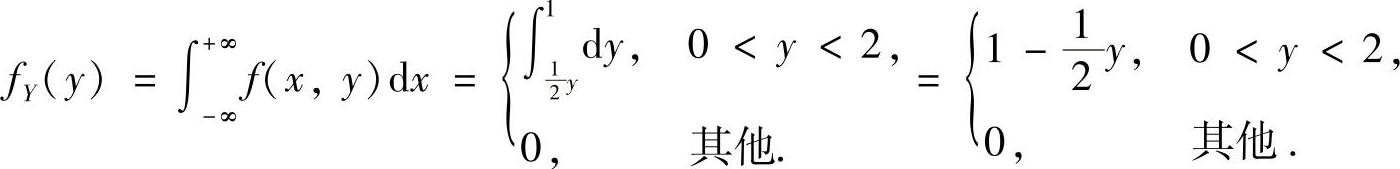
（2）Z=2X-Y的概率密度

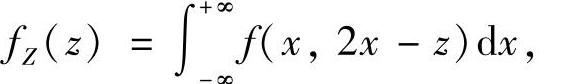
其中 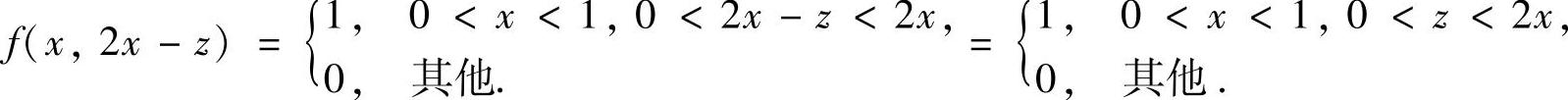所以，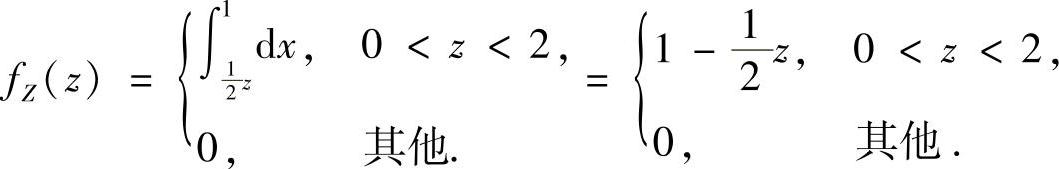

例13.3 设在随机变量Y=y∈（0，1）的条件下，随机变量X的条件概率密度为

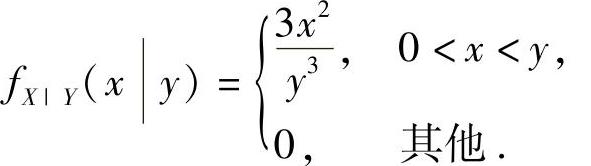
而Y的概率密度为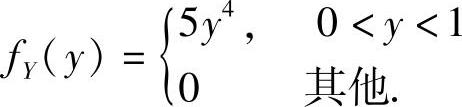，求X的概率密度f_X（x）.

精解 先算出（X，Y）的概率密度f（x，y），然后再计算f_X（x）.

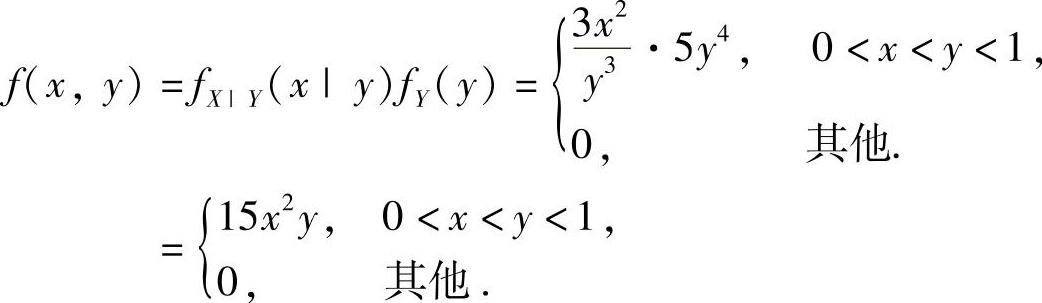
所以，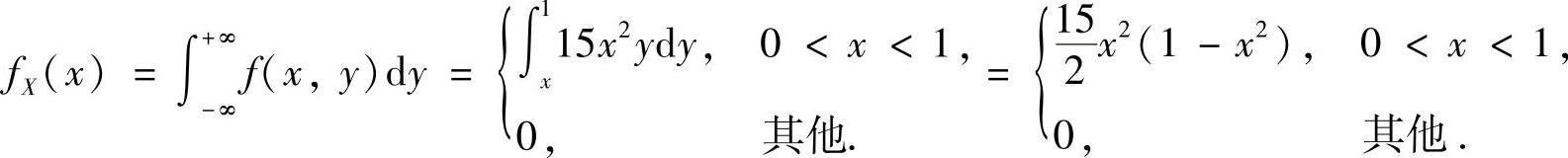

例13.4 设二维随机变量（X，Y）的概率密度为

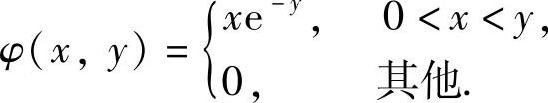
求随机变量U=max{X，Y}的概率密度f（u）.

精解 设U的分布函数为F（u），则

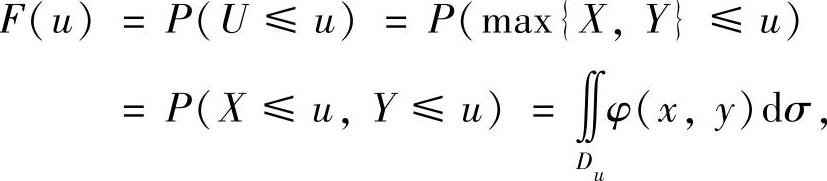
其中D_u={（x，y）|x≤u，y≤u}.此外，记D={（x，y）|0<x<y}.于是

当u≤0时，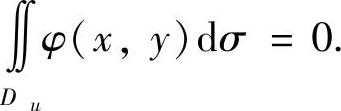

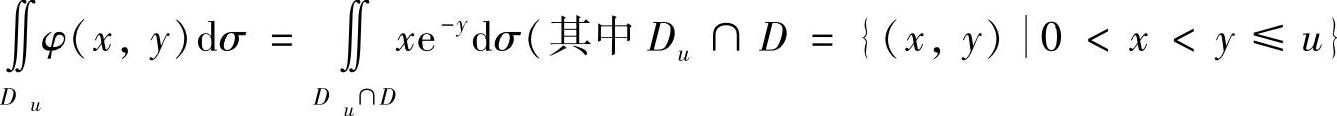
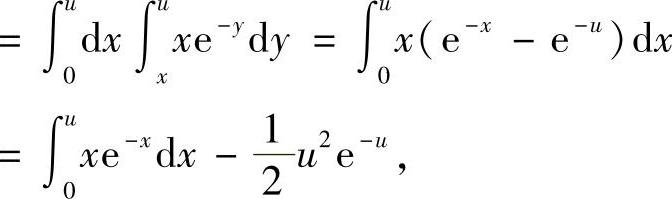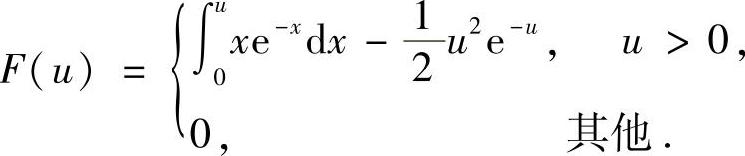当u>0时，所以，因此，