2008年全国硕士研究生入学统一考试试题精解

2008年全国硕士研究生入学统一考试试题精解

一、选择题

（1）分析 计算极限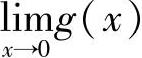即可.

精解 x=0是函数g（x）的间断点，由于

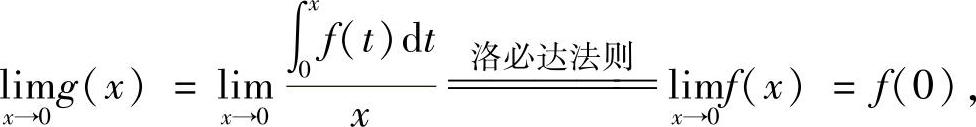
所以x=0是g（x）的可去间断点.

因此本题选（B）.

附注 设x₀是函数φ（x）的间断点，如果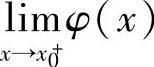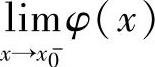，都存在，则称x₀是φ（x）的第一类间断点.特别地，当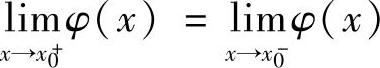（即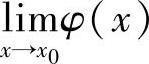存在）时，称x₀是φ（x）的可去间断点；当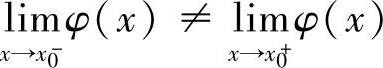时，称x₀是φ（x）的跳跃间断点.

（2）分析 先用分部积分法计算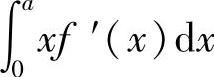，然后用定积分的几何意义确定正确的选项.

精解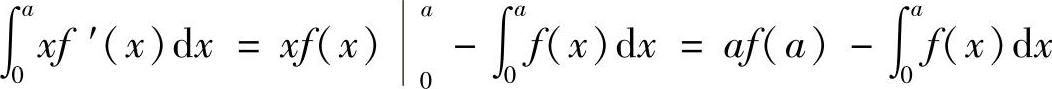

=矩形OBAC的面积-曲边梯形OBAD的面积

=曲边三角形ACD的面积.

因此本题选（C）.

附注 当f（x）≥0（x∈[a，b]）时，

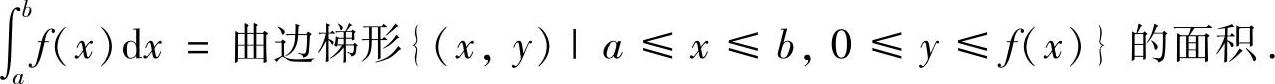理解定积分的几何意义有时可快捷地算得定积分，例如，当a>0时，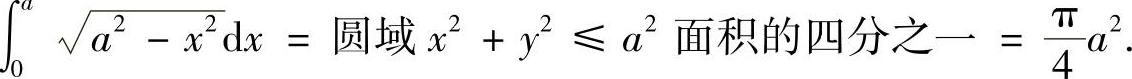

（3）分析 用定义计算f′_x（，0，0）和f′_y（0，0），确定正确选项.

精解 由于

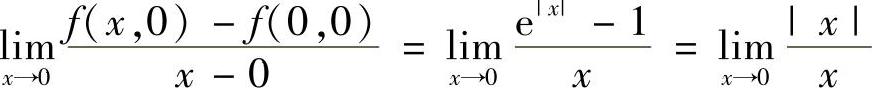
不存在，所以f′_x（0，0）不存在.

由于

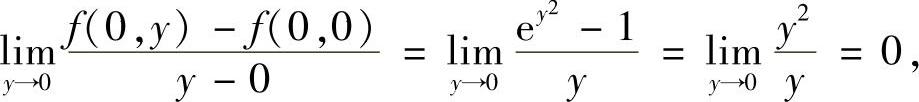
所以f′_y（0，0）存在.

因此本题选（B）.

附注 计算函数f（x，y）在点（x₀，y₀）处的偏导数时，往往从定义出发.

（4）分析 用极坐标将F（u，v）表示成积分上限函数，然后计算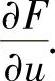

精解 由于

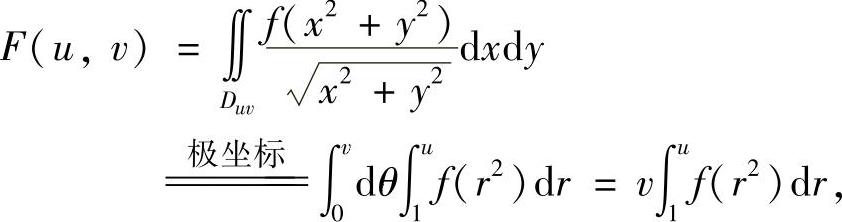
所以，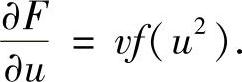

因此本题选（A）.

附注 由于积分区域D_uv是角域的一部分，且被积函数是x²+y²的函数，所以宜用极坐标计算所给的二重积分.

（5）分析 由A³=O，按可逆矩阵定义判定正确选项.

精解 由A³=O得E-A³=E.即（E-A）（E+A+A²）=E，所以矩阵E-A可逆.

由A³=O得E+A³=E，即（E+A）（E-A+A²）=E，所以矩阵E+A也可逆.

因此本题选（C）.

附注 本题也可从矩阵A的特征值入手求解：

设λ是A的特征值，则由A³=O知λ满足λ³=0，从而λ=0，即A的特征值全为零，因此E-A与E+A的特征值都全为1.由此推得E-A与E+A都可逆.

（6）分析 从“实对称矩阵合同的充分必要条件是它们具有相同个数的正特征值与负特征值”入手选择正确选项.

精解 由于|A|=-3<0，所以A的两个特征值中必有一正一负.

由于

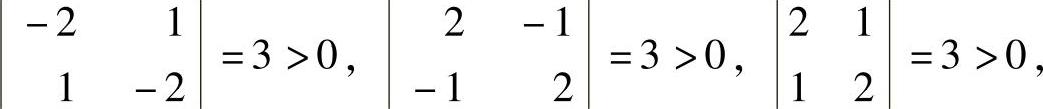
所以选项（A），（B），（C）的矩阵的特征值或全为正，或全为负，故矩阵A不可能与它们合同，应排除.

因此本题选（D）.

附注 记E是二阶单位矩阵，则

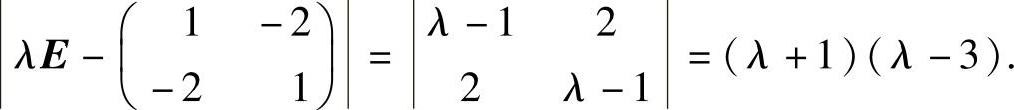
所以，选项（D）的矩阵的特征值为-1，3，确实是一正一负，因此A与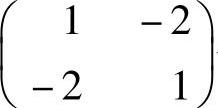合同.

（7）分析 按随机变量Z的分布函数定义确定正确选项.

精解 记Z的分布函数为F_Z（x），则 F_Z（x）=P（Z≤x）=P（max{X，Y}≤x）

=P（X≤x，Y≤x）=P（X≤x）P（Y≤x）=F²（x）.

因此本题选（A）.

附注 应记住以下结论：

设随机变量X，Y独立同分布，且X的分布函数为F（x），则U=max（X，Y）与V=min（X，Y）的分布函数分别为F²（x）与1-[1-F（x）]².

（8）分析 排除其中三个不正确选项即可.

精解 由ρ_XY=1知X与Y正相关，因此选项（A）、（C）排除.

如果Y=2X-1，则EY=E（2X-1）=2×0-1=-1，这不符合Y～N（1，4），所以选项（B）也应排除.

因此本题选（D）.

附注 这里给出选项（D）为正确的证明：

由于D（Y-2X）=DY-4DX=0，代入上式得1≥P（Y=2X+1）≥1，所以

P（Y=2X+1）=1.

二、填空题

（9）分析 只要利用函数f（x）在点c处连续即可确定c的值.

精解 由于函数f（x）在（-∞，+∞）上连续，特别在点x=c处连续，所以有

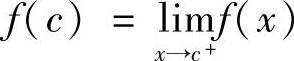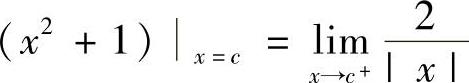,即 ，由此得到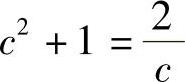，即c³+c-2=0，或者（c-1）（c²+c+2）=0.因此c=1.

附注 分段函数f（x）有两个分段点x=-c，c，但f（x）是偶函数，所以f（x）在点x=c处连续必在点x=-c处也连续，因此只要考虑点x=c即可.

（10）分析 先算出函数f（x）的表达式，再计算定积分.

精解 由于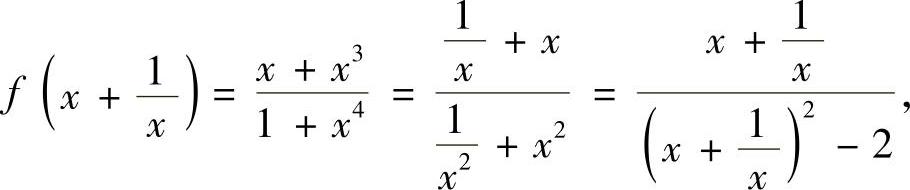

所以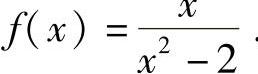

从而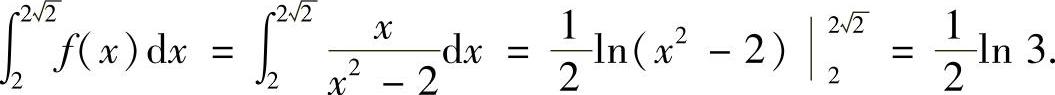

附注 由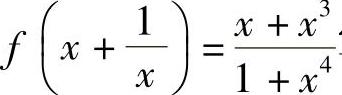写出f（x）的表达式问题，在初等数学中已多次见到过.

（11）分析 先利用D的对称性化简二重积分，然后用极坐标进行计算.

精解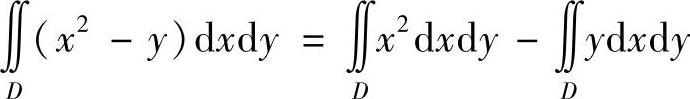

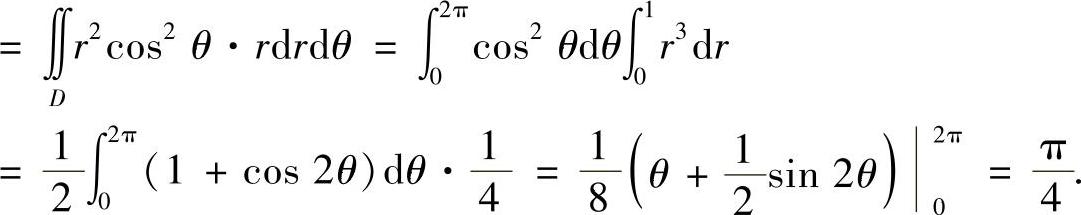
附注 对于二重积分而言，总是先按积分区域对称性进行化简，然后再计算.

（12）分析 所给微分方程可改写为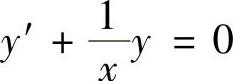，然后按一阶齐次线性微分方程通解公式计算即可.

精解 由于xy′+y=0可改写成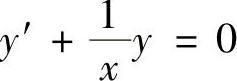.它的通解为

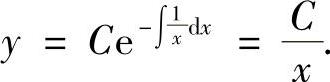
将y（1）=1代入上式得C=1.于是所求的解为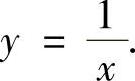

附注 所给微分方程也可改写成

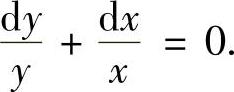
由此可得通解为lnxy=lnC，即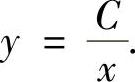

（13）分析 由矩阵A的特征值算出矩阵4A^-1-E的特征值，即可得到行列式|4A^-1-E|的值.精解 由矩阵A的特征值为1，2，2得A^-1的特征值为1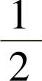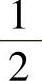，，，所以4A^-1-E的特征值为4×1-1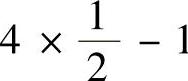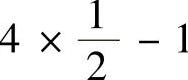，，，即3，1，1.因此

|4A^-1-E|=3×1×1=3.

附注 关于n阶矩阵A的特征值的以下结论是常用的：

（ⅰ）设A有特征值λ，则当A可逆时，A^-1有特征值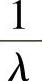，A^∗有特征值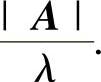

（ⅱ）设A有特征值λ，则f（A）=a₀Aⁿ+a₁A^n-1+…+a_n-1A+a_nE（E是n阶单位矩阵）有特征值f（λ）=a₀λⁿ+a₁λ^n-1+…+a_n-1λ+a_n.

（14）分析 按泊松分布及其数字特征计算.

精解 由于EX²=DX+（EX）²=1+1=2，所以

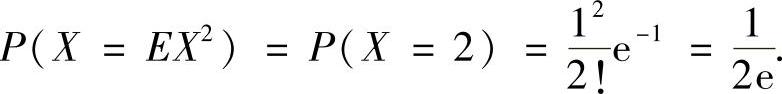
附注 要熟记以下结论：

当X～π（λ）时，X的概率分布为

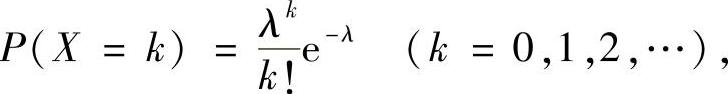
并且EX=DX=λ.

三、解答题

（15）分析 所给极限是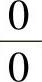型未定式极限，先用等价无穷小代替进行化简后再用洛必达法则计算.

精解 附注 计算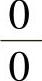型未定式极限时，总是先进行化简，其中用等价无穷小代替是化简的重要手段之一.

本题的有关计算方法见提高篇01.

（16）分析 （Ⅰ）将所给方程两边求全微分（利用全微分形式不变性），即可得到dz.

（Ⅱ）将（Ⅰ）中算得的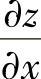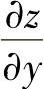，代入u后，计算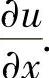

精解 （Ⅰ）将所给方程两边求全微分得

d（x²+y²-z）=dφ（x+y+z）.

利用全微分形式不变性得

2xdx+2ydy-dz=φ′（dx+dy+dz），

所以

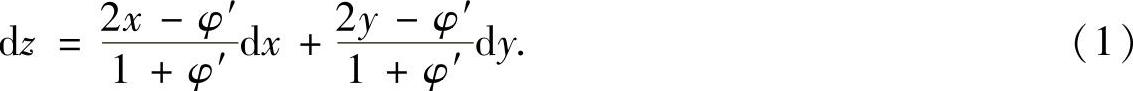
（Ⅱ）由式（1）可得

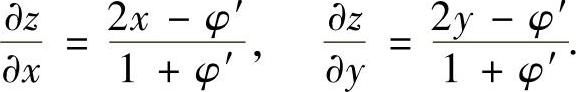
将它们代入u得

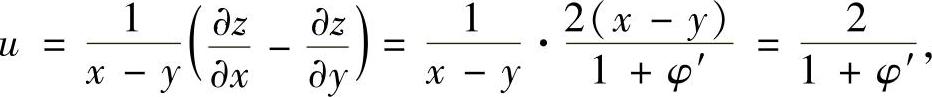
所以，

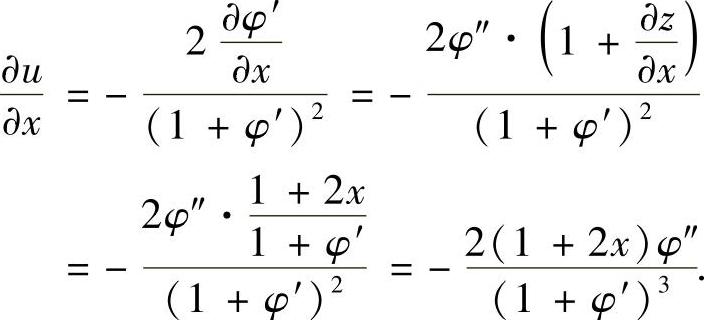
附注 计算由方程确定的隐函数z=z（x，y）的全微分，通常采用对方程两边求微分，然后利用全微分形式不变性算出全微分dz，这样做比较快捷.

本题的有关计算方法见提高篇10.

（17）分析 将D用曲线xy=1划成两块，然后计算二重积分.

精解 将D用曲线xy=1划分成D₁与D₂，如图B.08.1所示，则

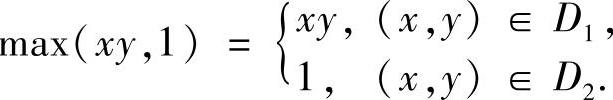
所以

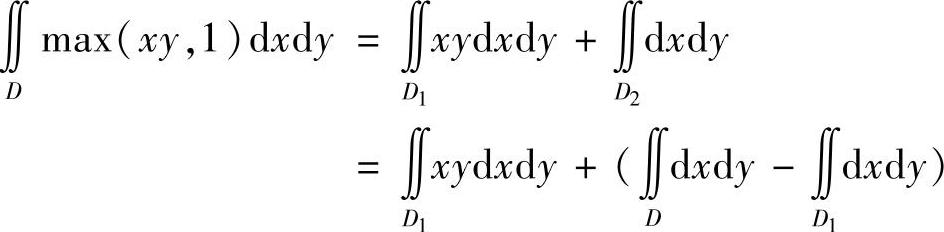
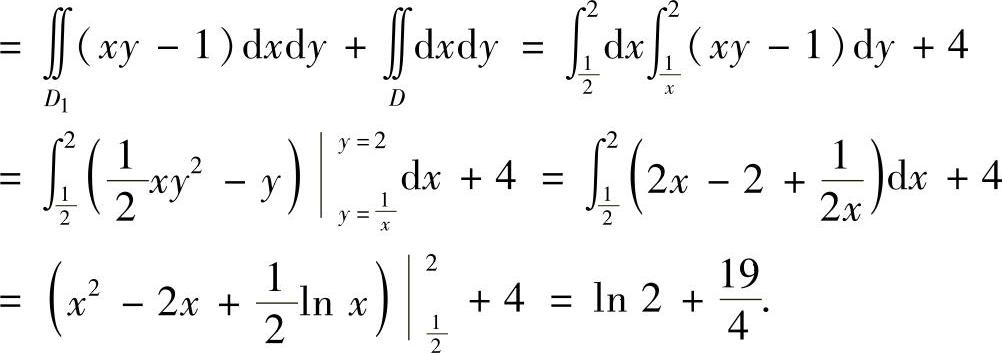
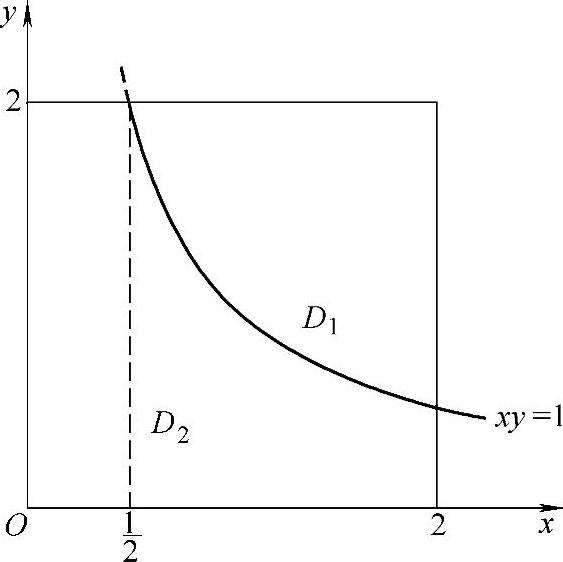
图 B.08.1

附注 二重积分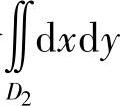也可直接计算，具体如下：

用直线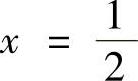将D₂划分成D₃与D₄两块（如图B.08.2所示），于是

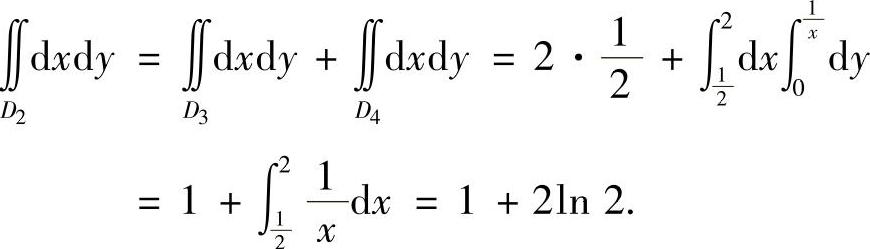
本题的有关计算方法见提高篇12.

（18）分析 （Ⅰ）由于

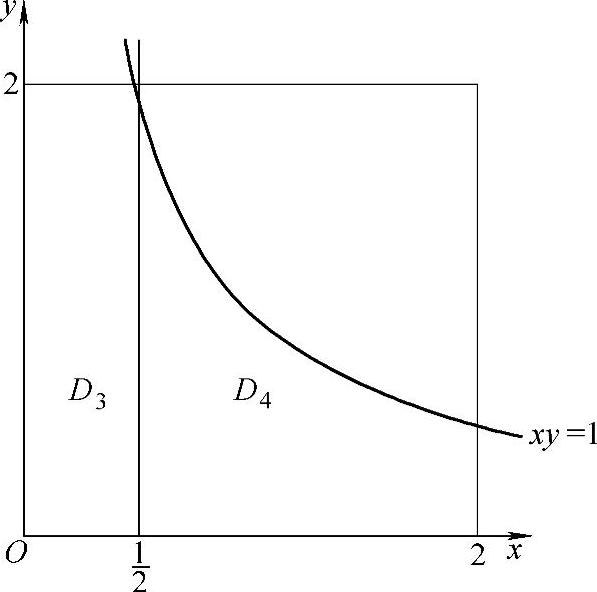
图 B.08.2

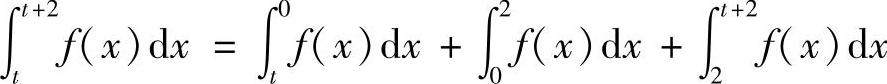
所以只要证明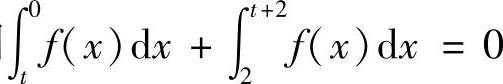即可.

（Ⅱ）只要证明对任意x∈（-∞，+∞），有G（x+2）=G（x）即可.

精解 （Ⅰ）由于

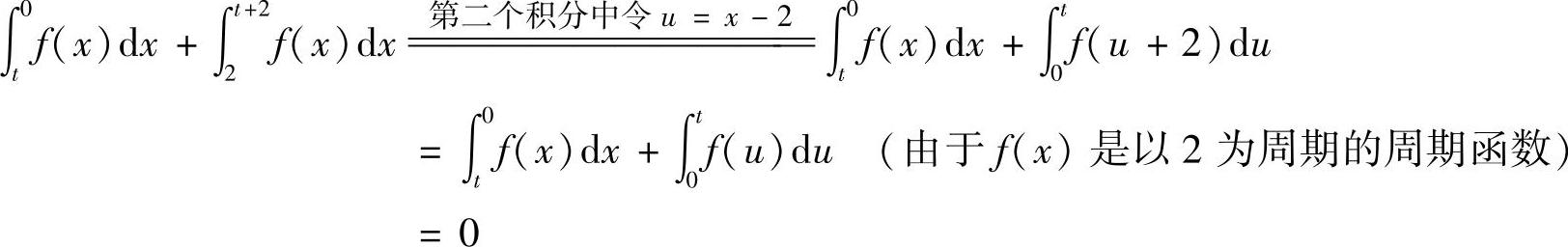
所以，对任意t∈（-∞，+∞）有

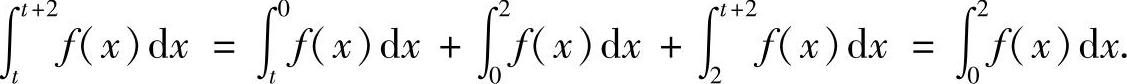
（Ⅱ）对任意x∈（-∞，+∞），有

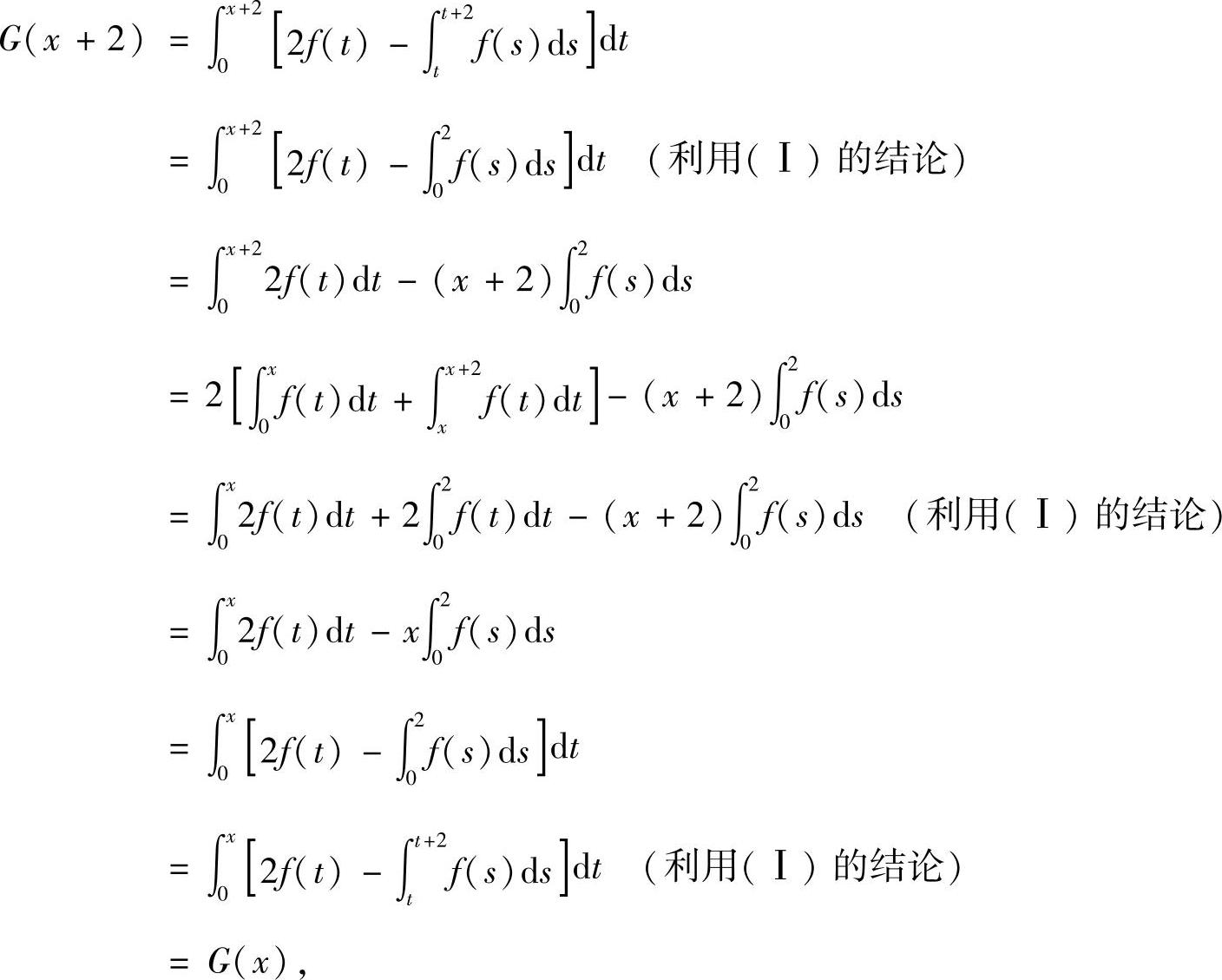
所以G（x）是以2为周期的周期函数.

附注 设φ（x）是周期为T的周期函数，则它有以下的积分性质：

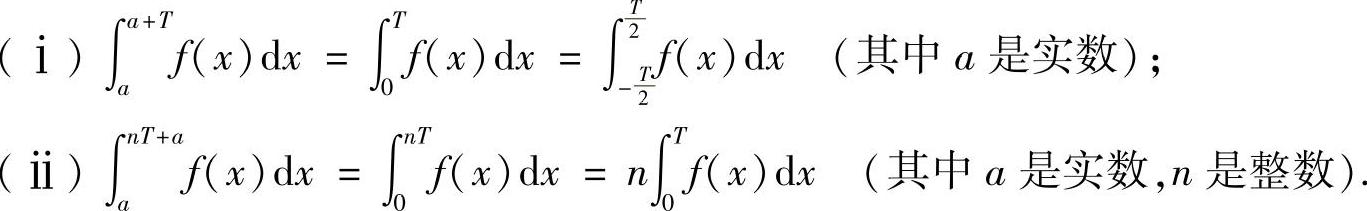
本题的有关计算方法见提高篇07.

（19）分析 第一年能提取19万元，则一开始至少存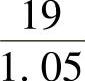万元，

第二年能提取28万元，则一开始至少存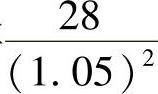万元，

︙

第n年能提取10+9n万元，则一开始至少存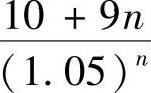万元，

︙

由此可以推出A至少是多少万元.

精解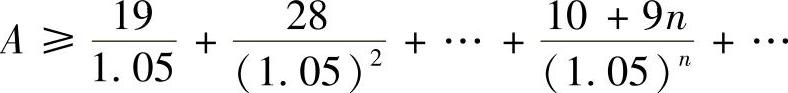

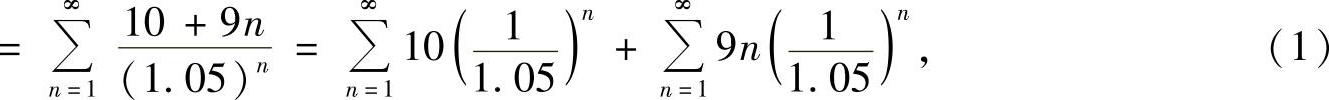
其中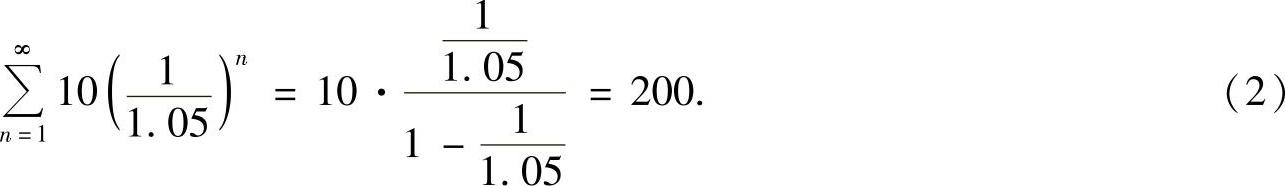

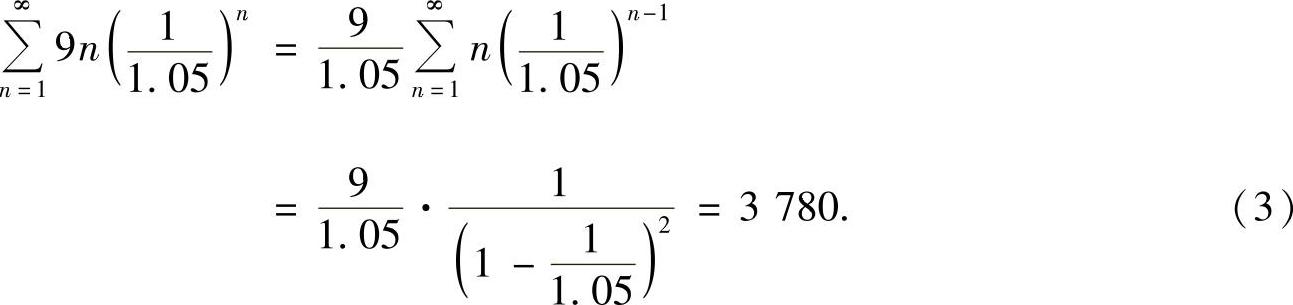
将式（2）、式（3）代入式（1）得

A≥200+3780=3980，

即A至少应为3980万元.

附注 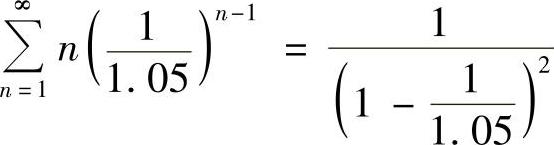的计算如下：

当0<x<1时，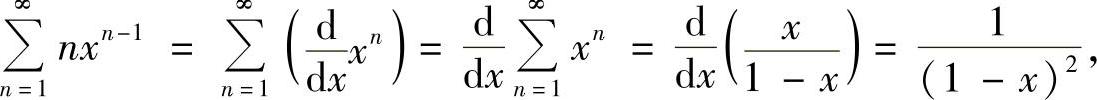

所以

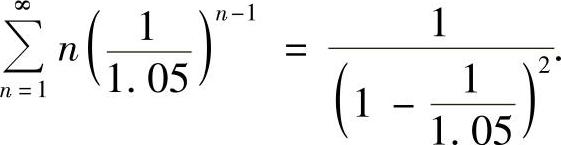
（20）分析 （Ⅰ）利用行列式性质将A化为上三角形行列式后算出|A|.

（Ⅱ）由|A|≠0算出Ax=b有唯一解的a值，并由克莱姆法则算出x_1.

（Ⅲ）由|A|=0算出Ax=b有无穷多解的a值.将求得的a值代入Ax=b计算通

解.

精解 （Ⅰ）

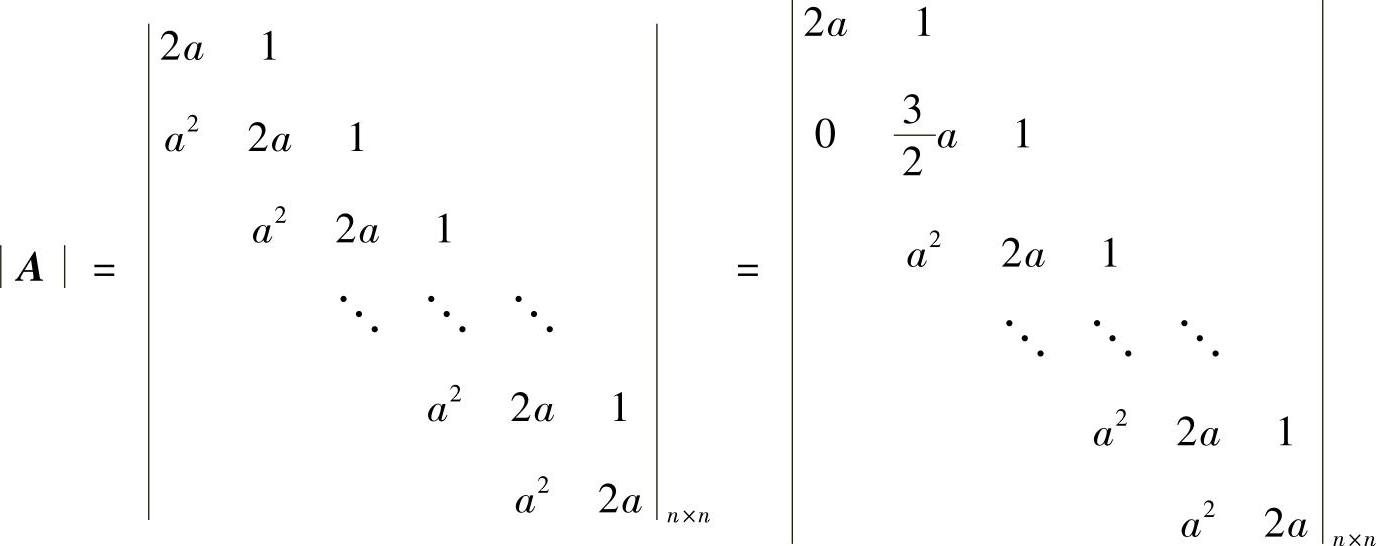
（Ⅱ）当a≠0时，|A|≠0，所以此时方程组Ax=b有唯一解，且由克莱姆法则得

其中

将式（2）代入式（1）得

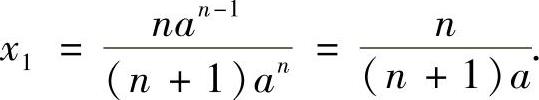
（Ⅲ）当a=0时，方程组Ax=b成为

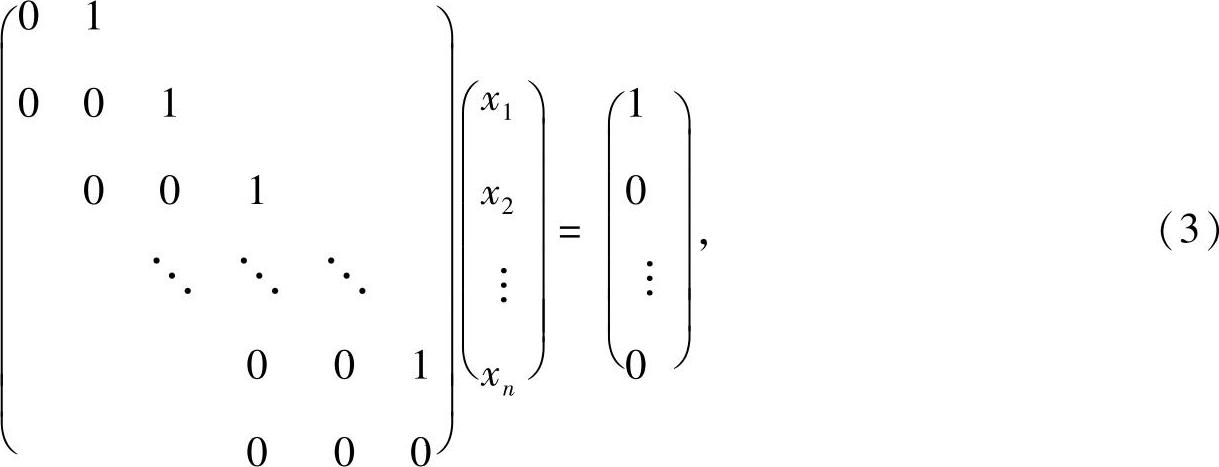
它即为方程组

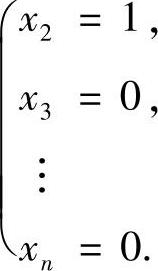
由此可知，方程组（3）有无穷多解，其通解为

附注 n阶行列式D_n通常有两种计算方法：

（ⅰ）利用行列式性质将D_n化为三角形行列式.

（ⅱ）按一行（或一列）展开D_n.

（21）分析 （Ⅰ）用定义证明α₁，α₂，α₃线性无关.

（Ⅱ）利用α₁，α₂都是A的特征向量及Aα₃=α₂+α₃，可以由A（α₁，α₂，α₃）=（α₁，α₂，α₃）B得到P^-1AP=B.

精解 （Ⅰ）设有数k₁，k₂，k₃，使得

k₁α₁+k₂α₂+k₃α₃=0，（1）

于是有

A（k₁α₁+k₂α₂+k₃α₃）=0，即k₁Aα₁+k₂Aα₂+k₃Aα₃=0，

将Aα₁=-α₁，Aα₂=α₂（因为α₁，α₂是A的对应特征值-1，1的特征向量），Aα₃=α₂+α₃代入上式得

-k₁α₁+k₂α₂+k₃（α₂+α₃）=0，即-k₁α₁+（k₂+k₃）α₂+k₃α₃=0.（2）

式（1）-式（2）得

2k₁α₁-k₃α₂=0.（3）

由于α₁，α₂是A的不同特征值的特征向量，所以线性无关，从而由式（3）得

k₁=k₃=0.

将它们代入式（1）得k₂α₂=0.由于α₂是A的特征向量，且不为零向量，所以k₂=0.

因此要使式（1）成立，必须满足k₁=k₂=k₃=0.由此推得α₁，α₂，α₃线性无关.

（Ⅱ）由α₁，α₂，α₃线性无关知，矩阵P=（α₁，α₂，α₃）可逆，且

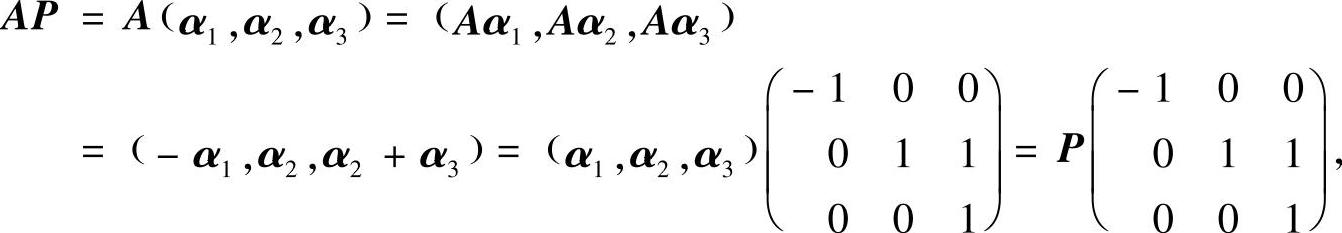
所以，

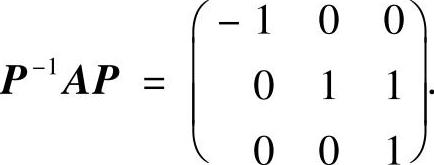
附注 由题解可知，A是不可相似对角化的.这是因为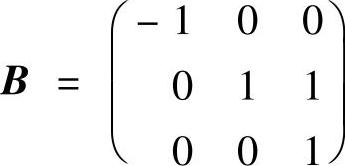有特征值λ=-1和λ=1（二重），但n-2=3-2≠r（1·E-B）=2（其中E是三阶单位矩阵），所以B不可相似对角化.

本题是综合题，其有关内容及计算方法见提高篇19.

（22）分析 （Ⅰ）由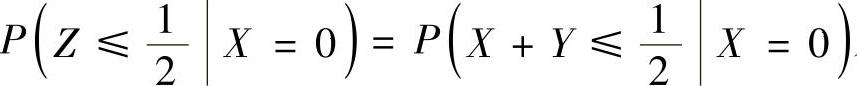及已知条件可以算出要求的条件概率.

（Ⅱ）先按分布函数算出随机变量Z的分布函数，然后计算它的概率密度.

精解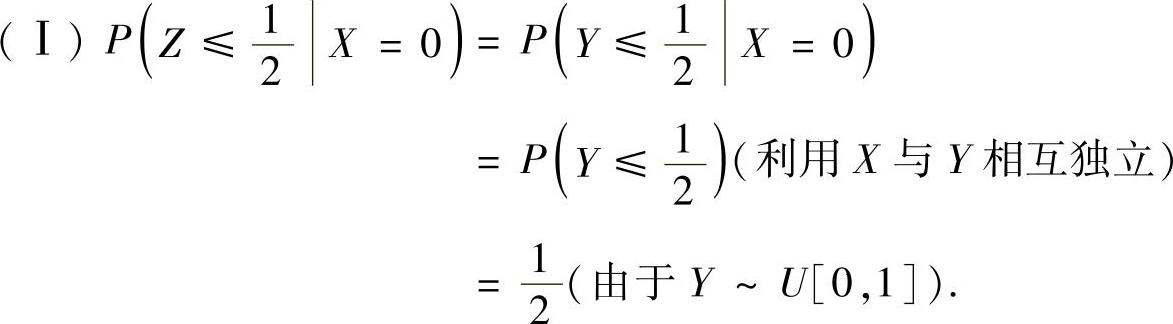

（Ⅱ）先计算随机变量Z的分布函数F_Z（z），然后求导得到它的概率密度f_Z（z）.

由于Y的分布函数

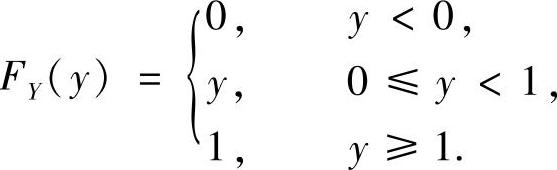
所以有

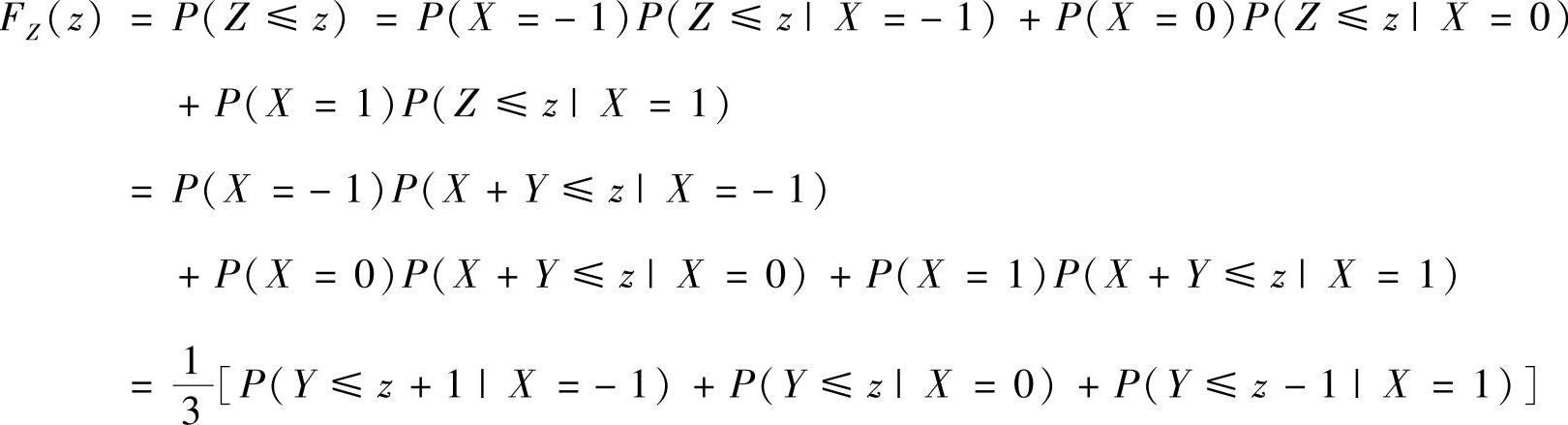
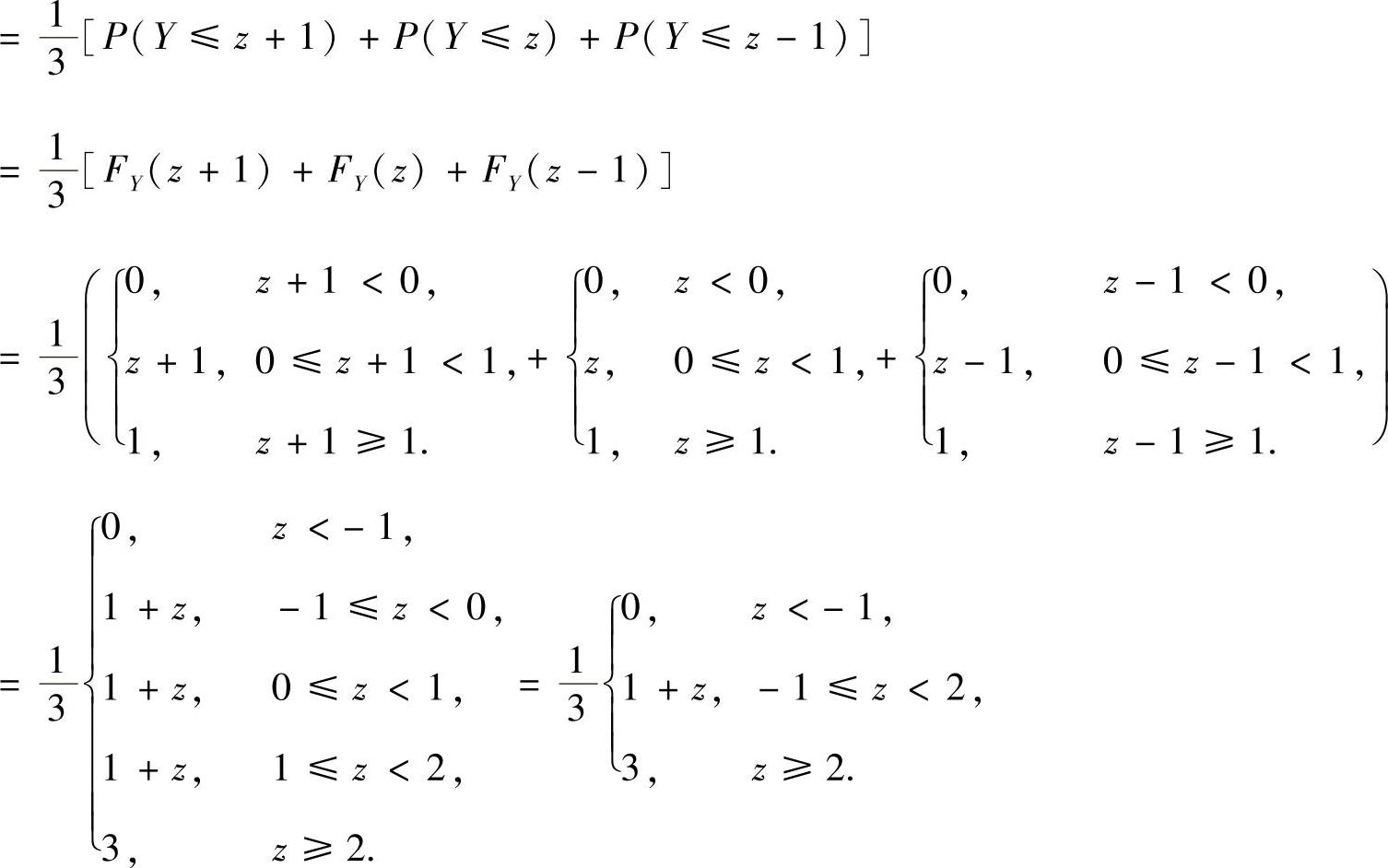
从而

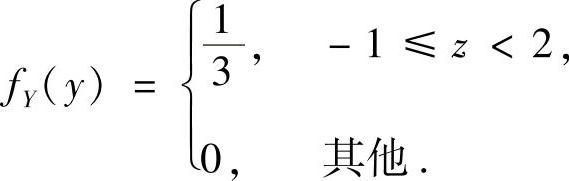
附注 由于Z=X+Y是离散型随机变量X与连续型随机变量Y之和，所以要计算Z的概率密度应先计算Z的分布函数.

本题是综合题，其有关内容及计算方法见提高篇21，22.

（23）分析 （Ⅰ）计算ET，证明T是μ²的无偏估计量.

（Ⅱ）利用X～χ²（k）的DX=2k，算出DT.

精解 （Ⅰ）由于

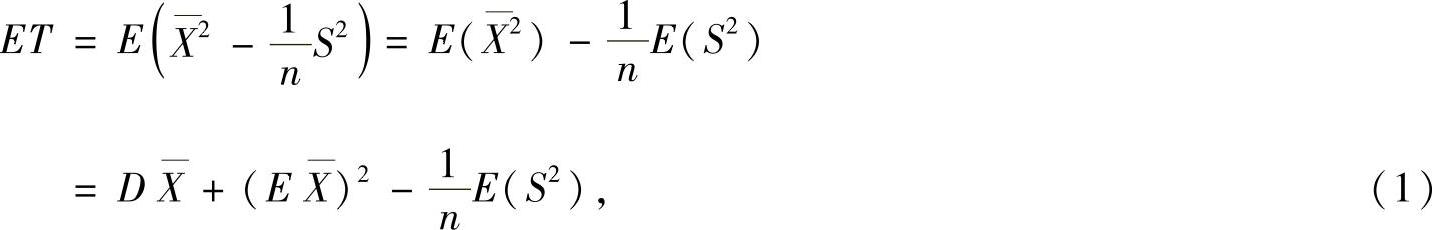
其中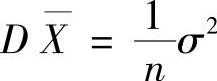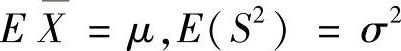，.将它们代入式（1）得

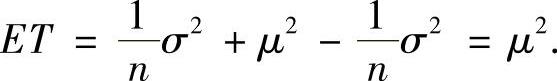
所以，T是μ²的无偏估计量.

（Ⅱ）当μ=0，σ=1时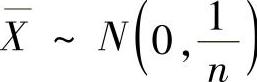，，所以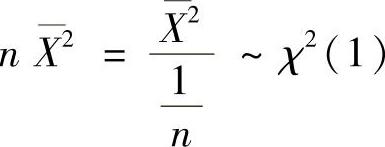.此外（n-1）S²～χ²（n-1），并且由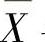与S²相互独立知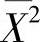与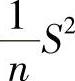相互独立，所以

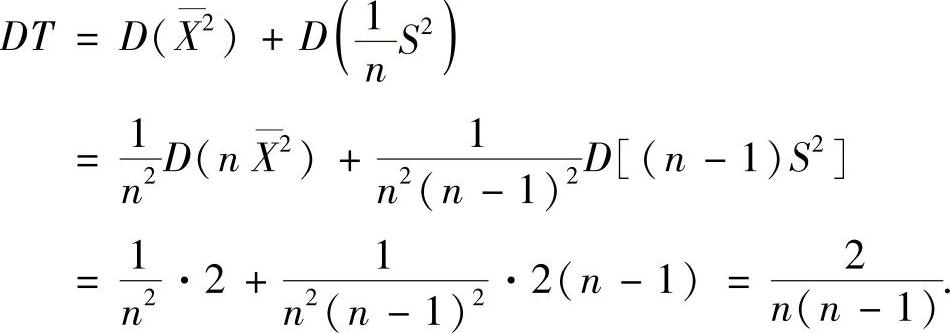
附注 设X₁，X₂，…，X_n是来自正态总体N（μ，σ²）的随机样本，则它的均值X和方差S²有以下性质：

（ⅰ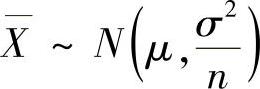），（n-1）S²～χ²（n-1），并且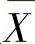与S²相互独立.

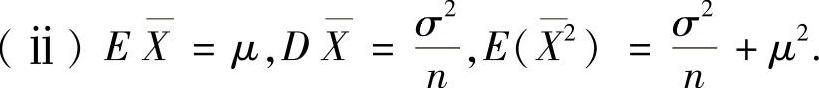
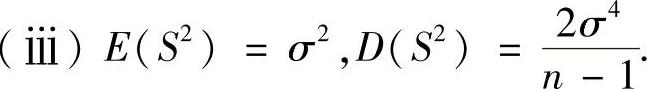
本题是综合题，其有关内容及计算方法见提高篇25，26.