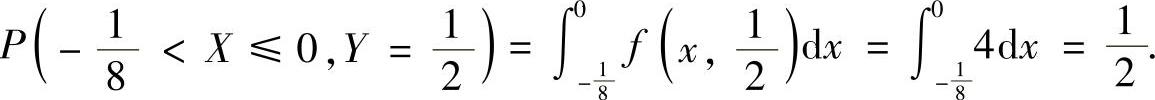各类随机事件概率的计算

12.各类随机事件概率的计算

随机事件的概率通常应用以下公式计算：

（1）逆事件概率公式（逆概公式）

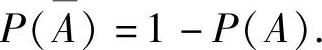
（2）加法公式

P（A∪B）=P（A）+P（B）-P（AB），特别当A，B互不相容时，P（A∪B）=P（A）+P（B）.

P（A∪B∪C）=P（A）+P（B）+P（C）-P（AB）-P（AC）-P（BC）+P（ABC），特别当A，B，C两两互不相容时，P（A∪B∪C）=P（A）+P（B）+P（C）.

（3）减法公式

P（A-B）=P（A）-P（AB），特别当B⊂A时，P（A-B）=P（A）-P（B）.

（4）乘法公式

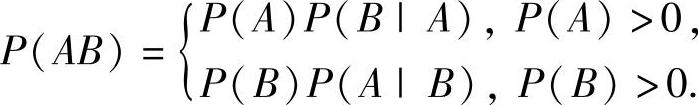
（5）全概率公式

设A₁，A₂，…，A_n是与事件B有关的完全事件组，且P（A_i）>0（i=1，2，…，n），则

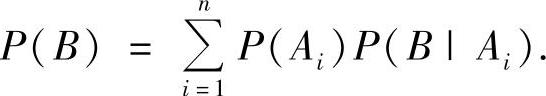
但是在考题中出现的往往是计算由随机变量表示的随机事件的概率，此时不仅需应用以上的公式，更需要利用随机变量的分布函数、概率分布（或概率密度）.

例12.1 有10个相同的罐子，其中有3个罐子都装有1个黑球1个红球，有6个罐子都装有2个黑球2个红球，有1个罐子装有9个红球1个黑球（球除颜色外，其余相同）.现任取一个罐子，再从这个罐子中任取一球，结果发现取出的是红球，求这个红球是从装有10个球的罐子中取出的概率.

精解 记 A={任取一球是红球}，

B₁={任取的罐子是装有2个球的}，

B₂={任取的罐子是装有4个球的}，

B₃={任取的罐子是装有10个球的}.

则要求的概率为

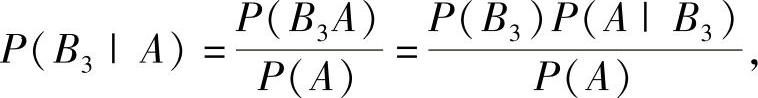
其中，B₁，B₂，B₃是与A有关的完全事件组，且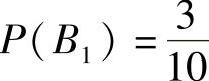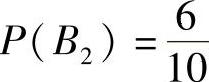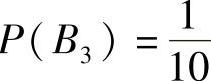，，，所以由全概率公式得

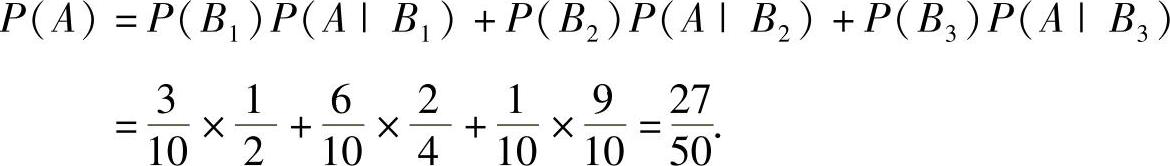
因此，所求的概率为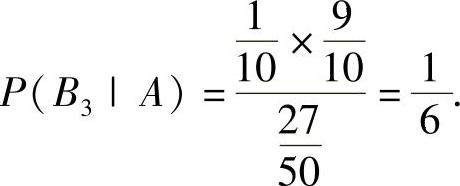例12.2 设A，B为随机事件，且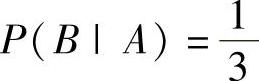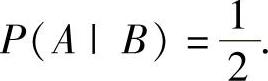，，记

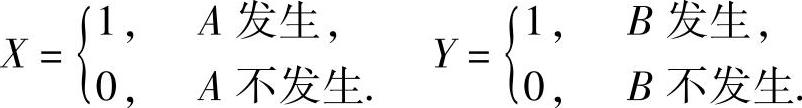
求二维随机变量（X，Y）的概率分布.

精解 本题实际上是计算随机事件概率的问题.

X，Y都只能取0和1两个值，且

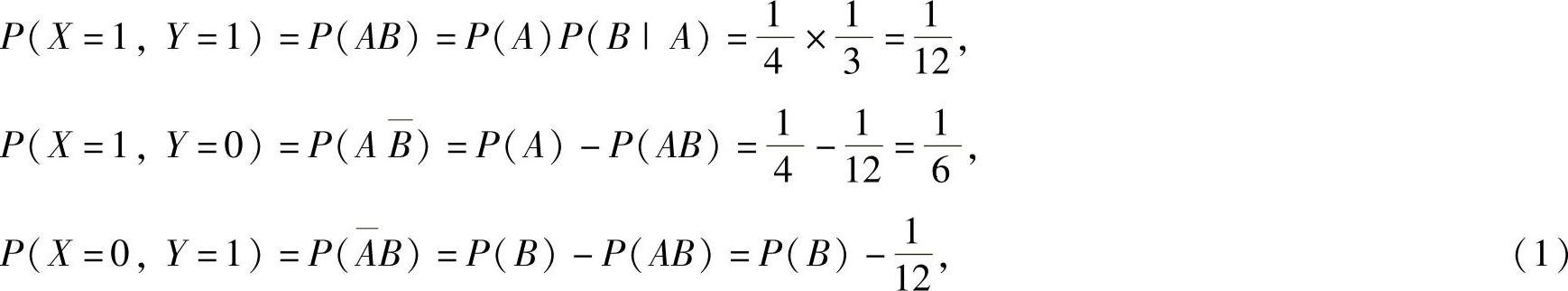
其中，由P（AB）=P（B）P（A|B）得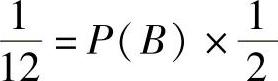，即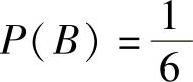.将它代入式（1）得

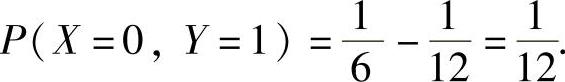(https://www.daowen.com)

此外，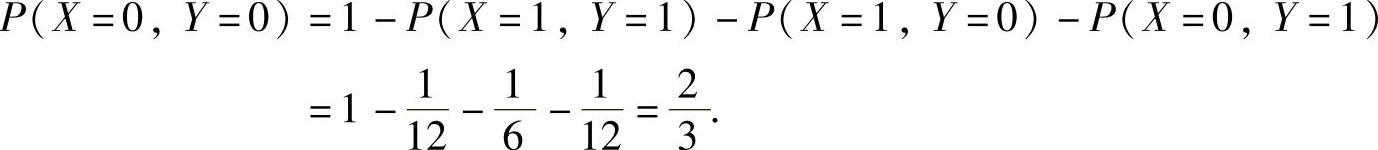

因此，（X，Y）的概率分布为

例12.3 设随机变量X～U[-1，3]，求随机变量Y=X³的分布函数F_Y（y）.

精解 X的概率密度为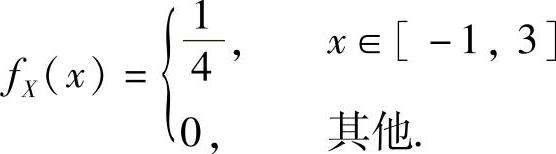，按定义计算F_Y（y），所以本题实际

上是计算随机事件概率的问题.

F_Y（y）=P（Y≤y）=P（X²≤y）.下面计算概率P（X²≤y）.

当y<0时，P（X²≤y）=P（∅）=0.

当y≥0时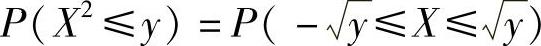，，于是

当0<y<1时，；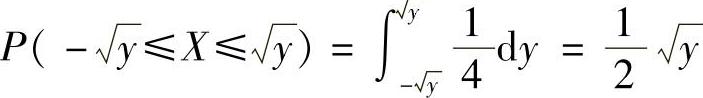

当1≤y<9时，；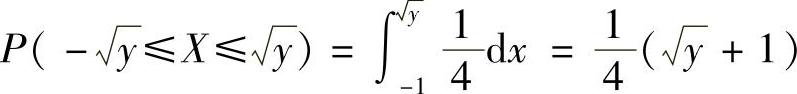

当y≥9时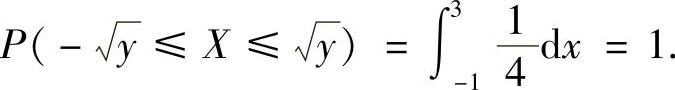，因此 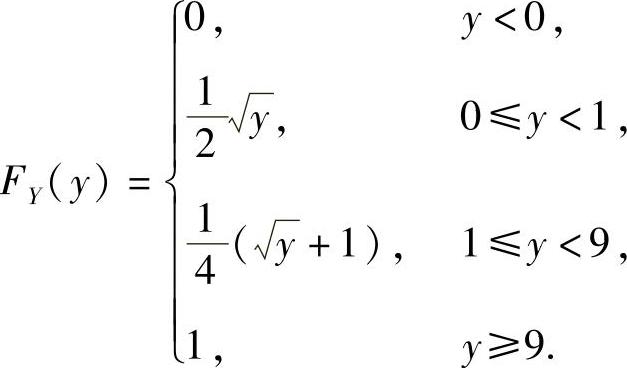例12.4 计算下列各题：

（1）设随机变量X与Y相互独立，X的概率分布为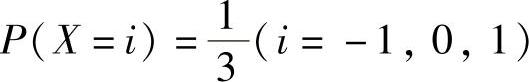，Y的概率密度为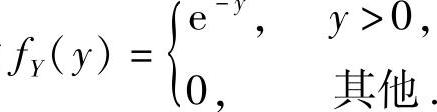记Z=X+Y，求概率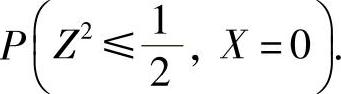

（2）设二维随机变量（X，Y）的概率密度为

求概率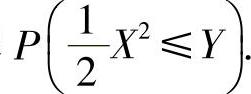

精解 （1）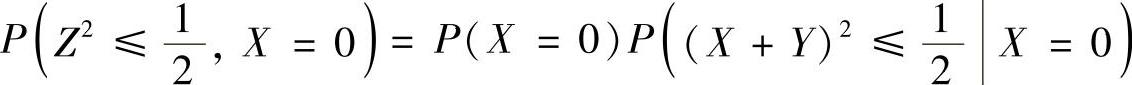

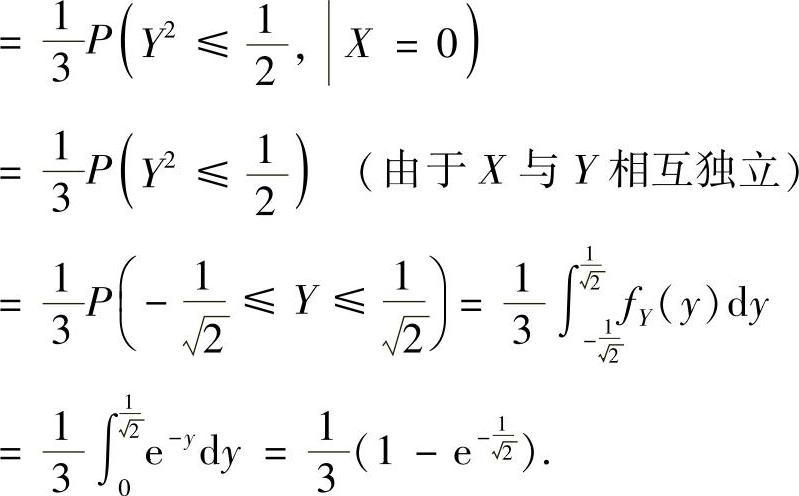
（2）记D={（x，y）0≤x≤1，0≤y≤1}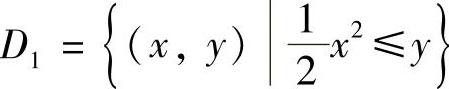，，则D∩D₁如图C.12.1的阴影部分所示.所以

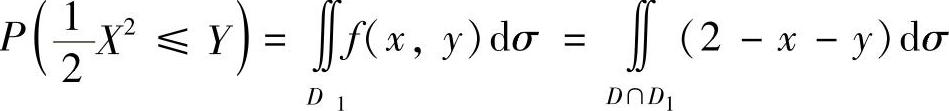
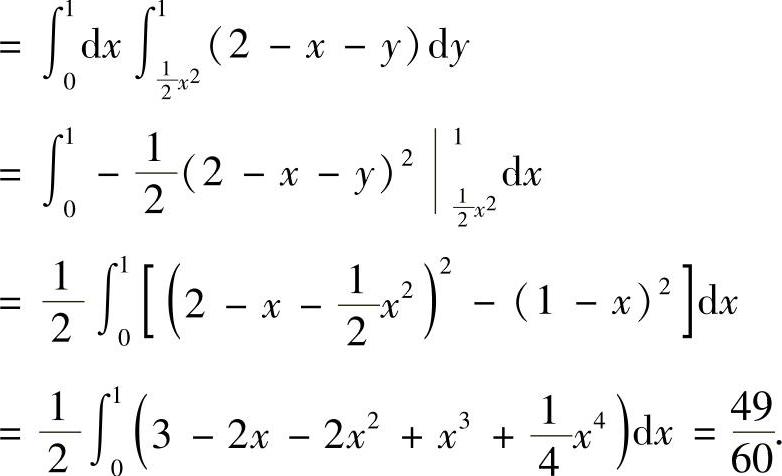
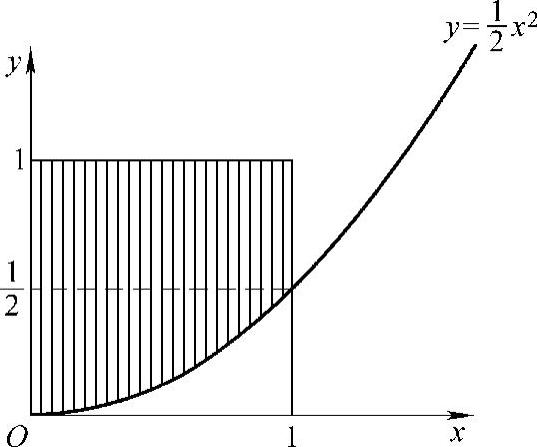
图 C.12.1

例12.5 设二维随机变量（X，Y）在区域G上服从均匀分布，其中G是由x轴、y轴以及直线y=2x+1围成的三角形.求条件概率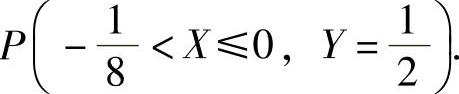

精解 先算出（X，Y）的条件概率密度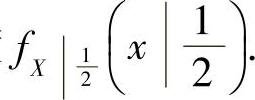为此画出G的图形如图C.12.2阴影部分所示.由于（X，Y）的概率密度

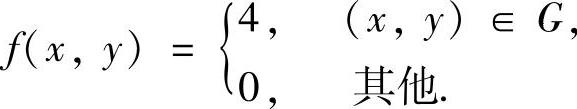
特别地，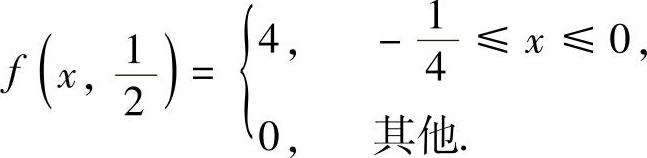

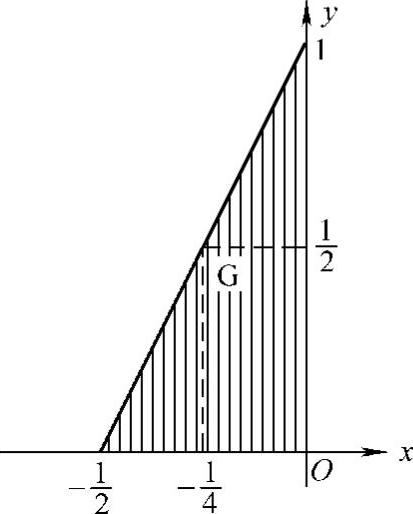
图 C.12.2

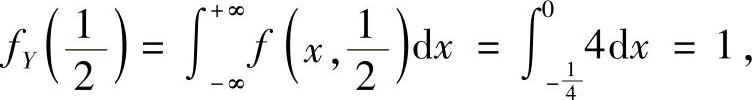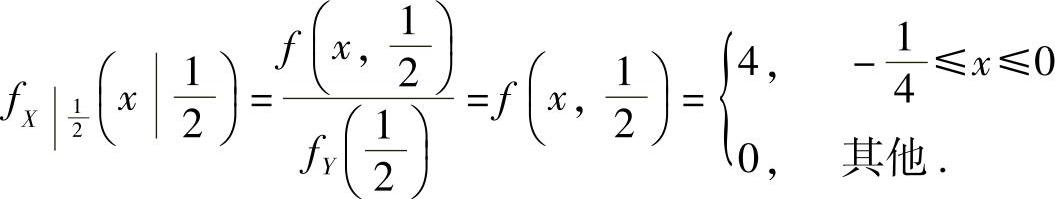此外，所以 ，因此