2011年全国硕士研究生入学统一考试试题精解
一、选择题
(1)分析 利用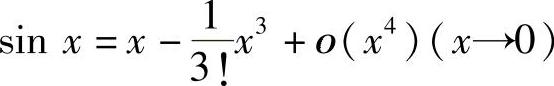 计算函数f(x)当x→0时的等价无穷小.
计算函数f(x)当x→0时的等价无穷小.
精解 由于
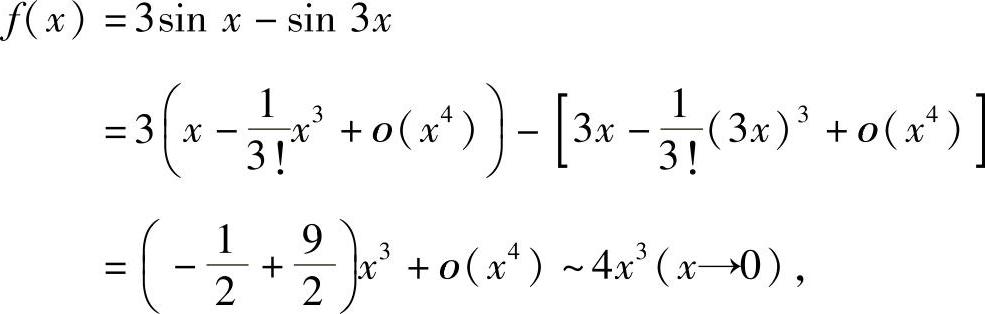
所以k=3,c=4.
因此本题选(C).
附注 本题也可以用洛必达法则逐一计算函数f(x)与x,x2,x3,…是否为同阶无穷小:
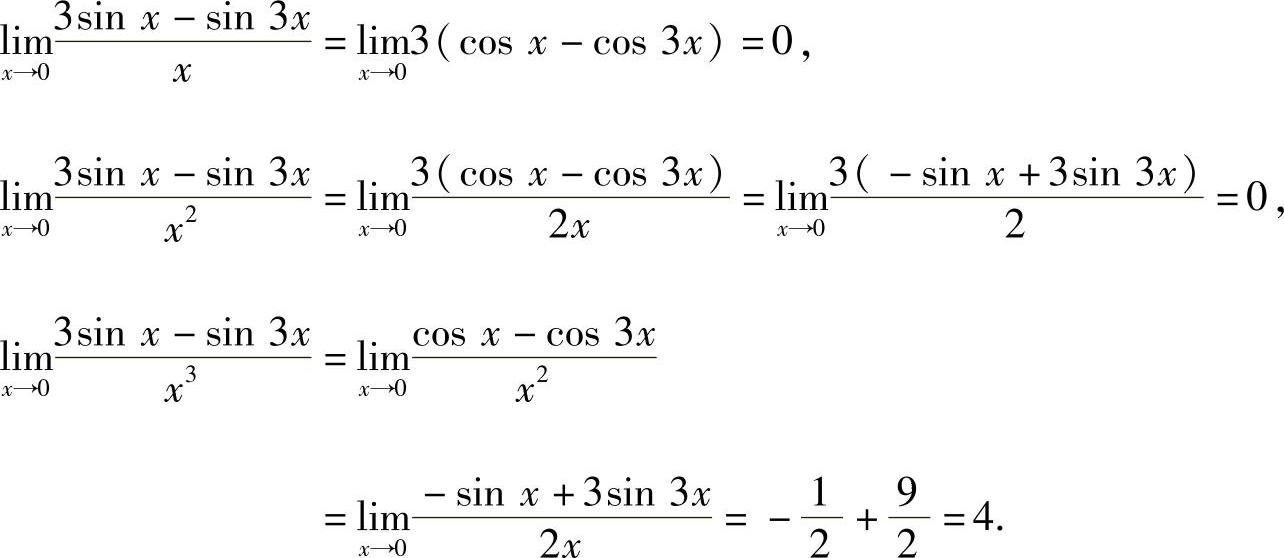
由此可知,f(x)=3sinx-sin3x~4x3(x→0),即k=3,c=4.
(2)分析 由于函数f(x)仅在点x=0处可导,因此需用导数定义计算所给的极限.
精解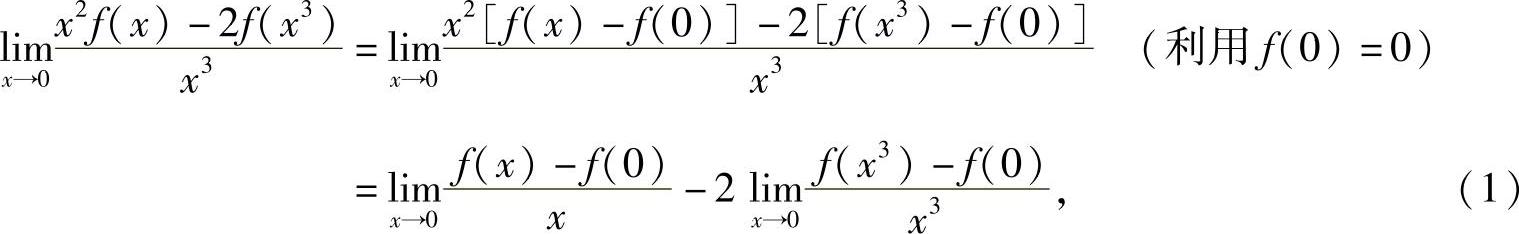
其中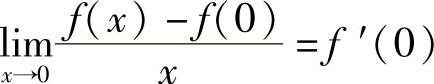 (利用f(x)在点x=0处可导),
(利用f(x)在点x=0处可导),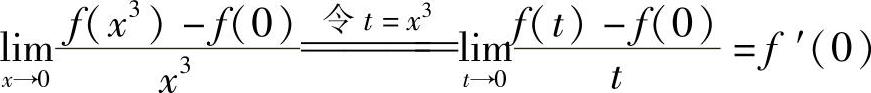 (利用f(t)在点t=0处可导).
(利用f(t)在点t=0处可导).
将它们代入式(1)得
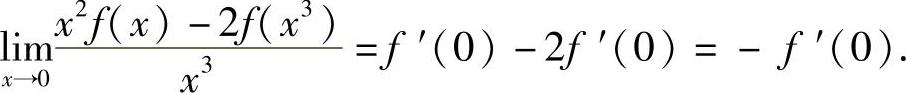
因此本题选(B).
附注 可考虑与本题类似的问题.
设函数f(x)在点x=1处可导,求极限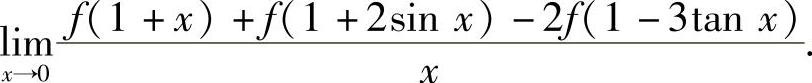 具体计算如下:
具体计算如下:
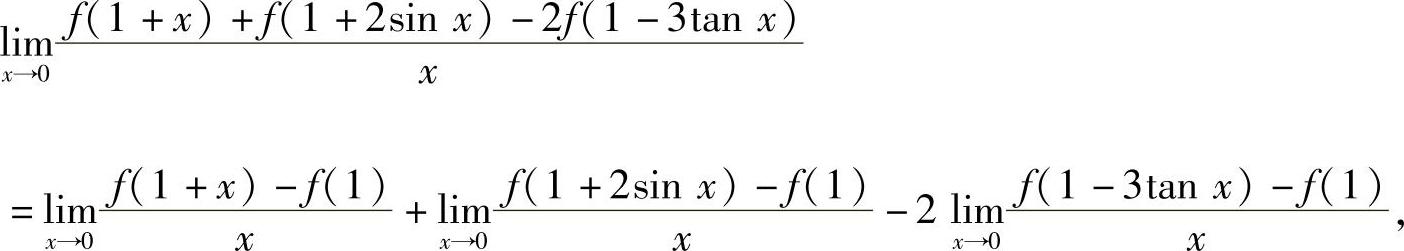
其中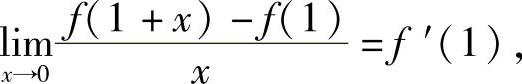
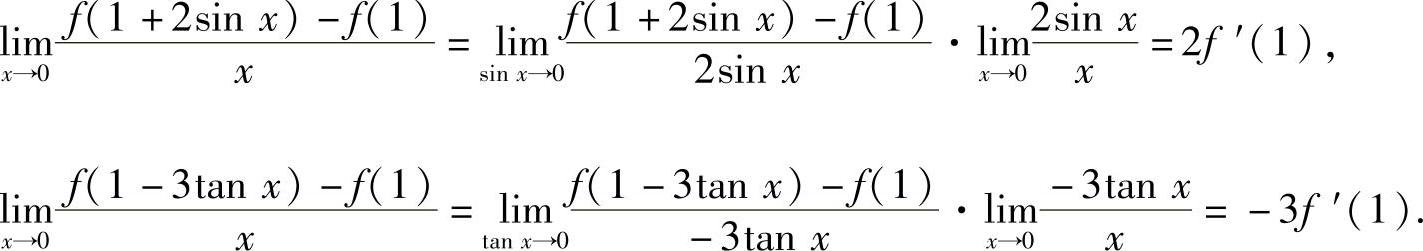
因此
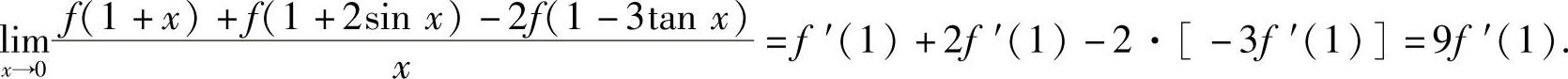
(3)分析 利用收敛级数性质判定.
精解 由于级数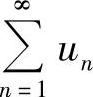 收敛,所以对它任意加括号后而成的级数仍收敛,特别是两项两项地加括号而成的级数
收敛,所以对它任意加括号后而成的级数仍收敛,特别是两项两项地加括号而成的级数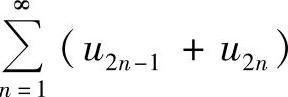 收敛.
收敛.
因此本题选(A).
附注 收敛级数有以下性质:
设级数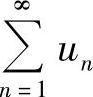 收敛,则对它任意加括号后所成的级数仍收敛.但反之未必成立,就是说,如果加括号后所成的级数收敛,则不能断定原来的级数也收敛.
收敛,则对它任意加括号后所成的级数仍收敛.但反之未必成立,就是说,如果加括号后所成的级数收敛,则不能断定原来的级数也收敛.
(4)分析 由于I,J,K都是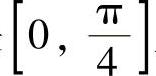 上的定积分,或仅有瑕点x=0的收敛的反常积分,所以只要比较被积函数在
上的定积分,或仅有瑕点x=0的收敛的反常积分,所以只要比较被积函数在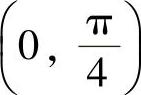 内的大小即可.
内的大小即可.
精解 由于对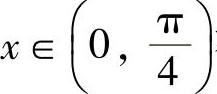 有
有
sin x<cos x<cot x,
所以由lnu是单调增加函数知
lnsin x<lncos x<lncot x.
于是
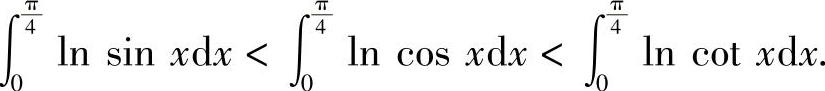
因此本题选(B).
附注 当函数f(x)与g(x)在[a,b]上连续时,如果f(x)<g(x)(x∈(a,b)),则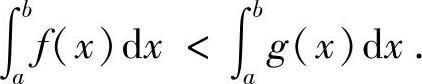
当函数f(x)与g(x)在(a,b]上连续时,如果x=a是f(x)或g(x)的瑕点,但作为反常积分的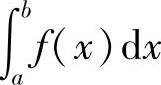 或
或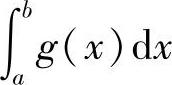 都收敛,并且f(x)<g(x)(x∈(a,b)),则
都收敛,并且f(x)<g(x)(x∈(a,b)),则
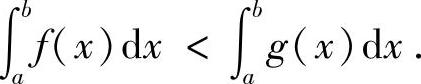
(5)分析 写出对应初等变换的初等矩阵,并进行运算即可.
精解 由题设知
AP1=B,P2B=E3 (E3是三阶单位矩阵),
所以,A=BP1-1=P2-1P1-1=P2P1-1(由于P2-1=P2).
因此本题选(D).
附注 应熟记矩阵的初等变换与初等矩阵之间的对应关系.
(6)分析 利用非齐次线性方程组解的构造判定正确选项.
精解 由于非齐次线性方程组Ax=β有3个线性无关的解η1,η2,η3,则η2-η1,η3-η1是对应的导出组Ax=0的两个线性无关的解,从而Ax=0的基础解系中至少有两个解.因此选项(A)、(B)都是不正确的.此外,容易看到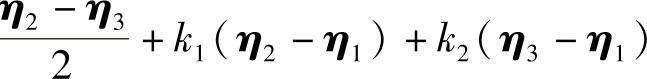 不是Ax=β的解,所以选项(D)应排除.
不是Ax=β的解,所以选项(D)应排除.
因此本题选(C).
附注 实际上,矩阵A的秩r(A)=1.证明如下:
由于Ax=0的基础解系中至少有两个解,所以r(A)≤3-2=1.
由于A是非零矩阵(线性方程组的系数矩阵必是非零矩阵),所以r(A)≥1.从而r(A)=1.
(7)分析 利用连续型随机变量的分布函数的导数为概率密度这一结论即可.
精解 由于F1(x),F2(x)都为分布函数时,F1(x)F2(x)也是分布函数,且它是可导函数,所以,其导数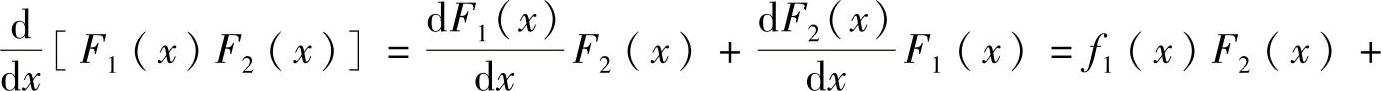
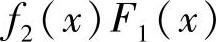 是概率密度.
是概率密度.
因此本题选(D).
附注 应记住以下结论:
如果F1(x),F2(x)都是分布函数,则F1(x)F2(x)也是分布函数.
(8)分析 只要分别计算ET1,ET2,DT1及DT2即可.计算时利用
EX=DX=λ.
精解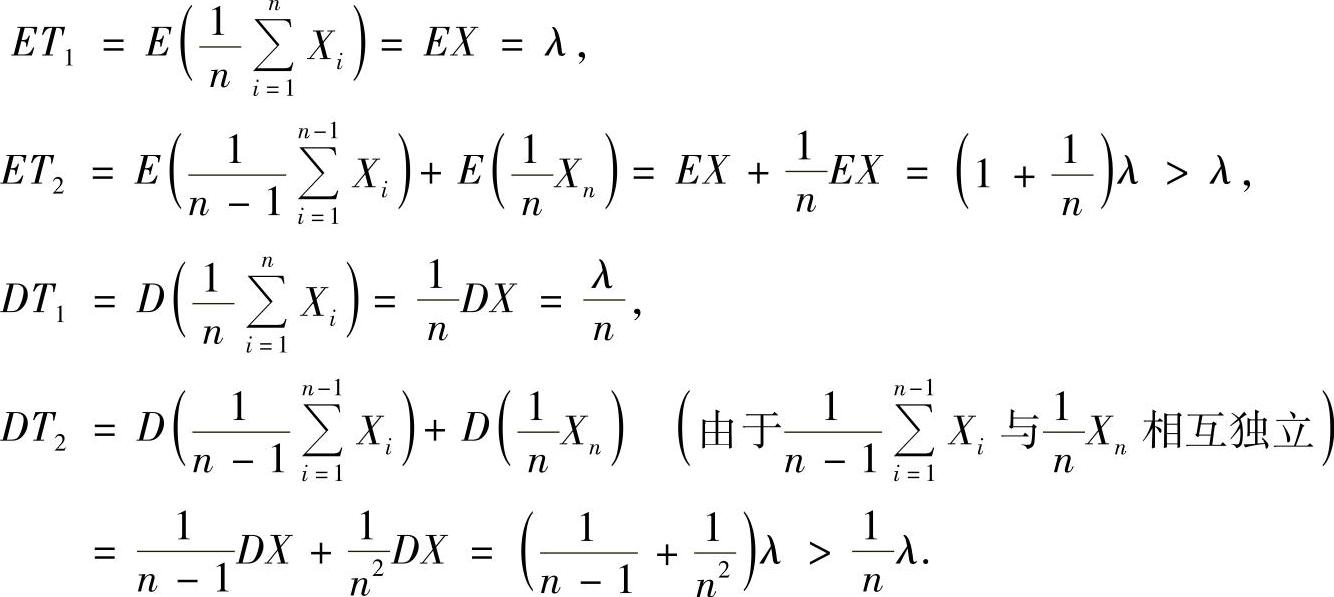
由此可知,ET1<ET2,DT1<DT2.
因此本题选(D).
附注 设X1,X2,…,Xn是来自总体X的简单随机样本,且X的数学期望与方差分别为μ,σ2,并记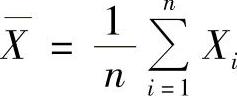 (样本均值),则
(样本均值),则
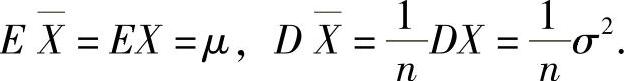
记住以上的结论.
二、填空题
(9)分析 先利用重要极限公式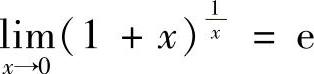 算出函数f(x)的表达式,然后求导.
算出函数f(x)的表达式,然后求导.
精解 由于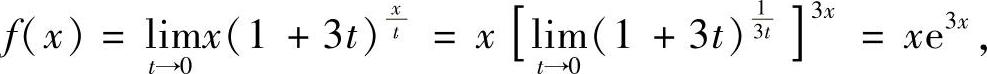 所以,f′(x)=(xe3x)′=(1+3x)e3x.
所以,f′(x)=(xe3x)′=(1+3x)e3x.
附注 重要极限公式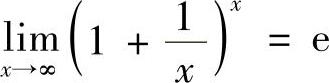 常表示为
常表示为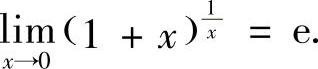
(10)分析 令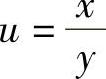 ,则z=(1+u)u=euln(1+u),然后利用一阶微分形式不变性计算dz.
,则z=(1+u)u=euln(1+u),然后利用一阶微分形式不变性计算dz.
精解 由于
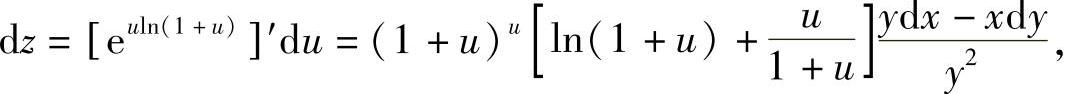
所以
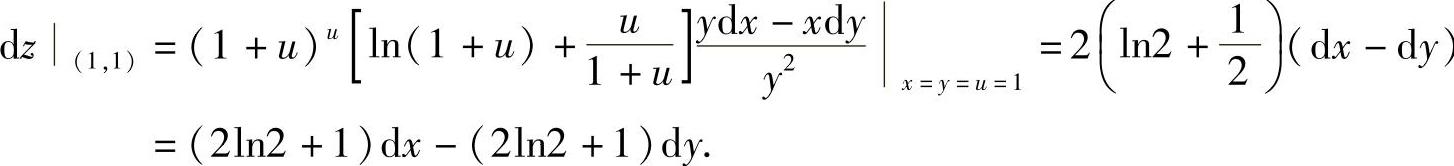
附注 利用一阶微分形式不变性往往能较快捷地算出复合函数微分.所谓微分形式不变性是指:
设f(u)是可微函数,则不管u是自变量或自变量的可微函数都有
df(u)=f′(u)du.
(11)分析 由隐函数求导算出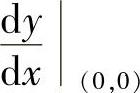 即可得到所求的切线方程.
即可得到所求的切线方程.
精解 所给方程两边对x求导得
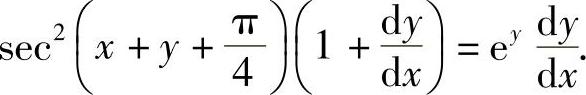
将x=y=0代入,上式成为
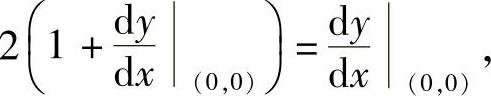
即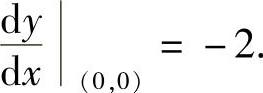
因此所求的切线方程为y-0=-2(x-0),即y=-2x.
附注 应熟练掌握隐函数求导数或微分的方法.
(12)分析 按旋转体体积公式计算.
精解 记由曲线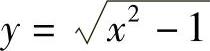 ,直线x=2及x轴所围成的平面图形为D,即
,直线x=2及x轴所围成的平面图形为D,即
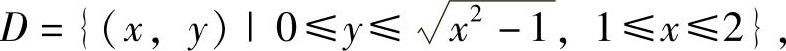
所以所求的体积为
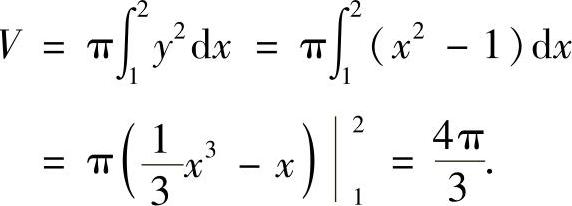
附注 记住以下的旋转体体积计算公式:
(ⅰ)平面区域D={(x,y)|a≤x≤b,0≤f1(x)≤y≤f2(x)}绕x轴旋转而成的旋转体体积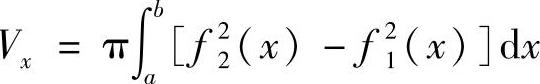 ;
;
(ⅱ)平面区域D={(x,y)|0≤a≤x≤b,f1(x)≤y≤f2(x)}绕y轴旋转而成的旋转体体积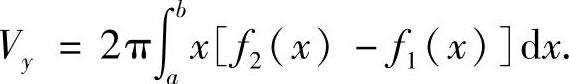
(13)分析 只要算出矩阵A的正交相似对角矩阵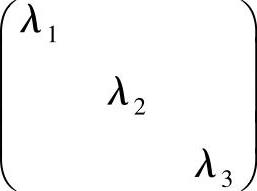 即可.
即可.
精解 由于A是实对称矩阵,它可正交相似对角化,即存在正交矩阵Q,使得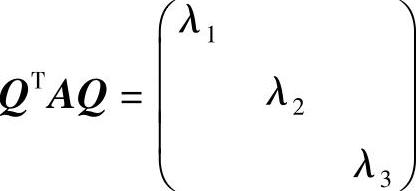 (其中λ1,λ2,λ3是A的特征值).
(其中λ1,λ2,λ3是A的特征值).
由于A的各行元素之和为3,所以有
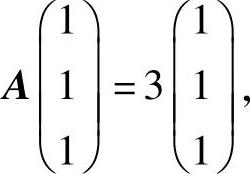
即A有特征值λ1=3.由于r(A)=1,所以λ2=λ3=0.因此
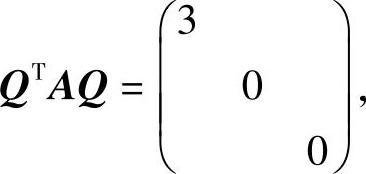
从而f在正交变换x=Qy(其中x=(x1,x2,x3),y=(y1,y2,y3)T)下的标准形为3y21.
附注 记住以下结论:
设n阶矩阵A的各行元素之和为k,则A有特征值k,且其对应的特征向量有
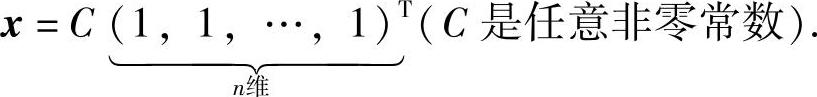
(14)分析 由ρ=0知服从正态分布的随机变量X与Y相互独立,由此即可算出E(XY2).
精解 由于(X,Y)~N(μ,μ;σ2,σ2;0)(注意ρ=0),所以X与Y相互独立,且都服从N(μ,σ2).从而有
E(XY2)=EX·EY2=EX[DY+(EY)2]=μ(σ2+μ2).
附注 二维正态分布的以下性质是常用的,应记住:
(ⅰ)当(X,Y)~N(μ1,μ2;σ21,σ22;ρ)时,X~N(μ1,σ21),Y~N(μ2,σ22).
(ⅱ)当(X,Y)~N(μ1,μ2;σ21,σ22;ρ)时,X与Y相互独立的充分必要条件是ρ=0.
(ⅲ)当X与Y相互独立,且X~N(μ1,σ21),Y~N(μ2,σ22),a,b是不全为零的常数时,aX+bY~N(aμ1+bμ2,a2σ21+b2σ22).
(ⅳ)当(X,Y)~N(μ1,μ2;σ21,σ22;ρ),a,b是不全为零常数时,aX+bY~N(aμ1+bμ2,a2σ21+bσ22+2abρσ1σ1).
三、解答题
(15)分析 所给极限是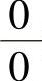 型未定式极限.利用函数
型未定式极限.利用函数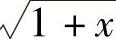
`及sinx的带佩亚诺型余项的麦克劳林公式寻找分子的等价无穷小后,用等价无穷小代替计算所给极限.
精解 由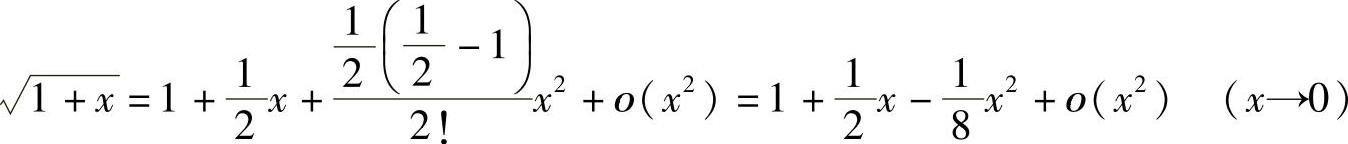 和sinx=x+ο(x3)知
和sinx=x+ο(x3)知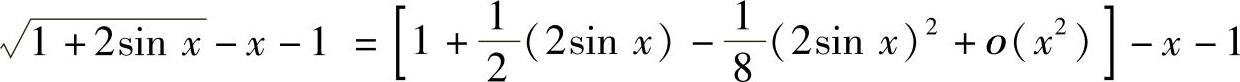
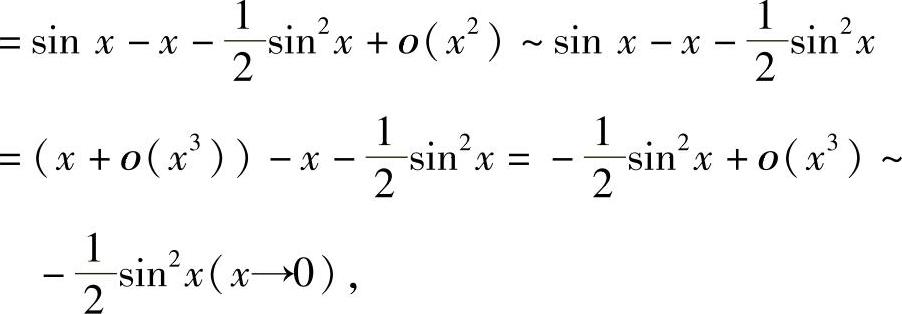
此外,xln(1+x)~x2(x→0),所以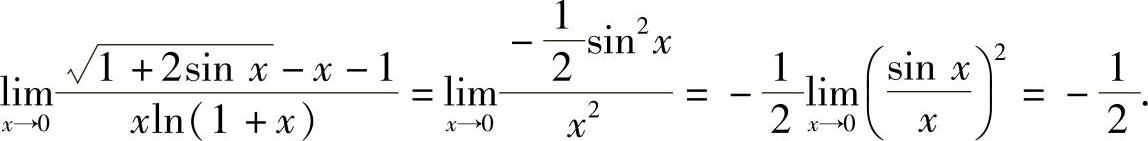 (https://www.daowen.com)
(https://www.daowen.com)
附注 利用五个常用函数的麦克劳林公式(带佩亚诺型余项),往往能快捷得到比较复杂的初等函数在x→0时的等价无穷小:
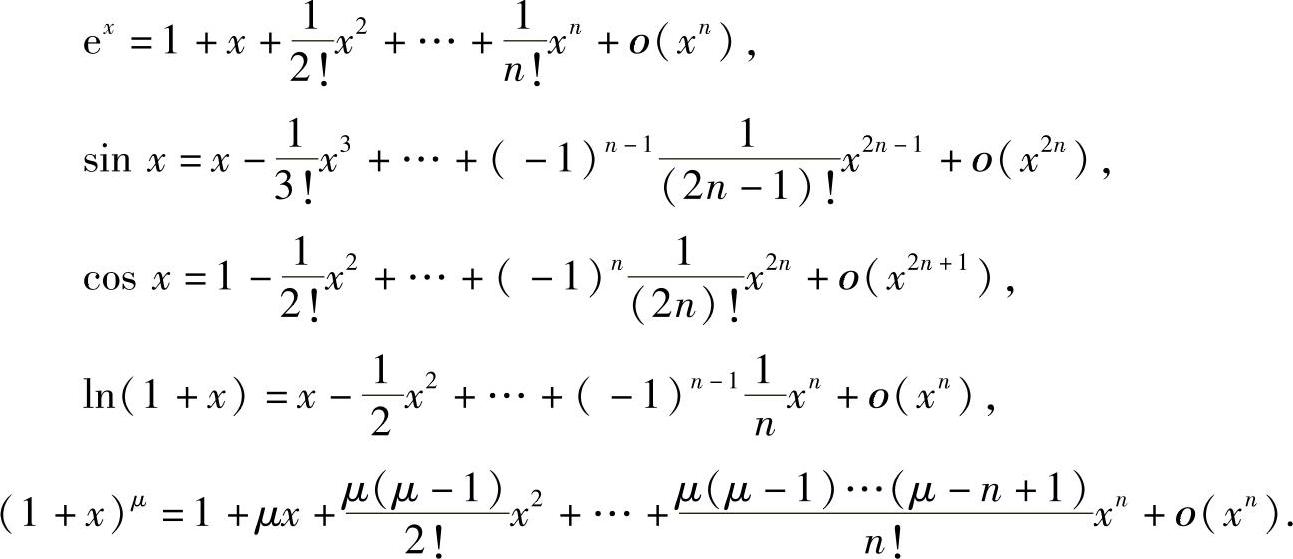
本题的有关内容及计算方法见提高篇01.
(16)分析 算出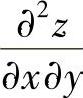 后,用f(1,1)=2,f1′(1,1)=f2′(1,1)=0代入即得
后,用f(1,1)=2,f1′(1,1)=f2′(1,1)=0代入即得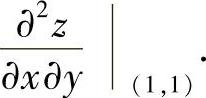
精解 由于
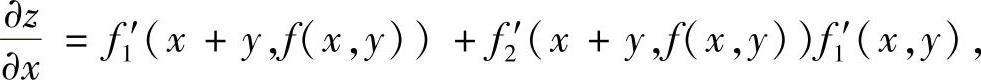
所以
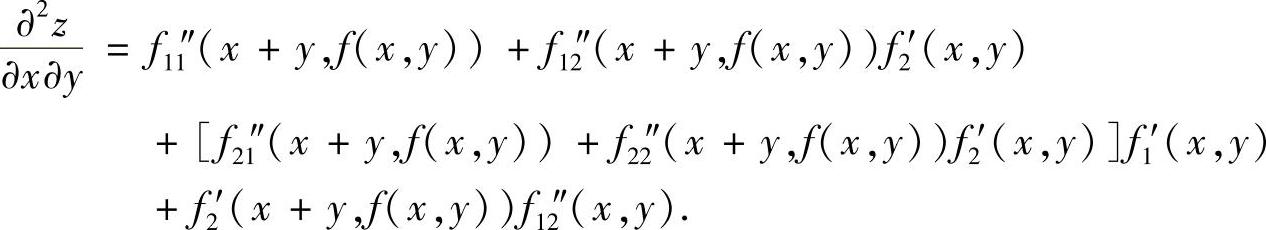
因此,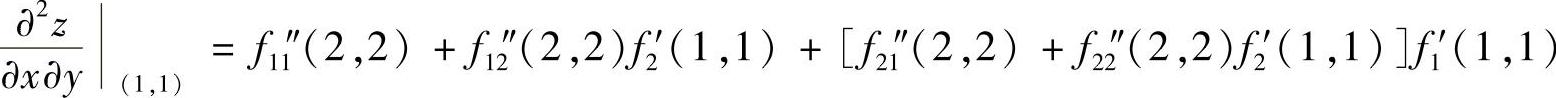
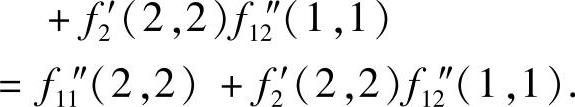
附注 应熟练掌握二元复合函数的一、二阶偏导数的计算.
(17)分析 先令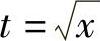 ,然后用分部积分法计算.
,然后用分部积分法计算.
精解 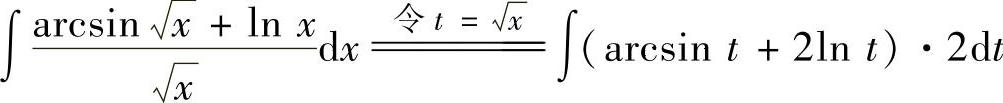
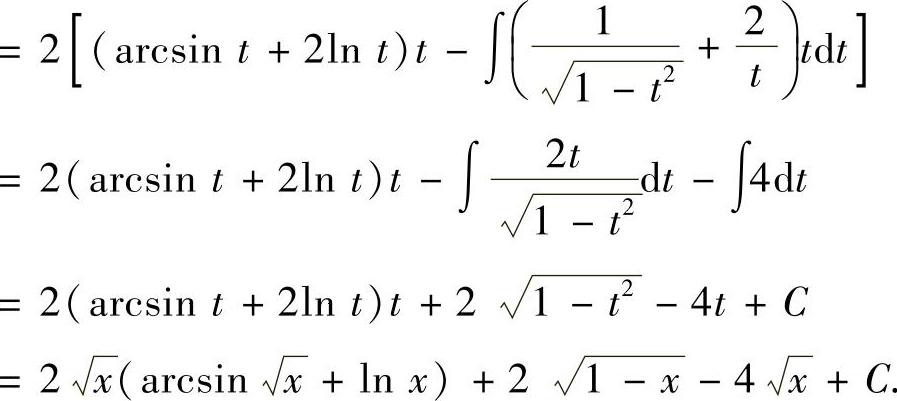
附注 当被积函数中含有无理式时,往往通过适当的变量代换,先去掉其中的无理式.此外,在不定积分计算中,往往综合运用换元积分法与分部积分法,使计算更快捷有效.
(18)分析 记函数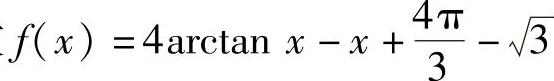 ,然后用导数方法证明方程f(x)=0恰有两个实根.
,然后用导数方法证明方程f(x)=0恰有两个实根.
精解 函数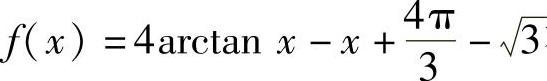 在(-∞,+∞)上可导,且
在(-∞,+∞)上可导,且
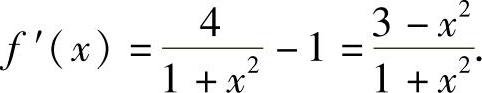
显然,f′(x)=0只有两个实根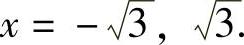 据此列表如下:
据此列表如下:

由表可知,方程f(x)=0有实根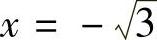 ,此外在
,此外在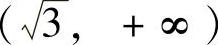 内还有一个实根,记为x0.由此证得方程f(x)=0恰有两个实根
内还有一个实根,记为x0.由此证得方程f(x)=0恰有两个实根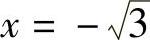 和x=x0.
和x=x0.
附注 计算函数f(x)在(a,b)内的单调区间、极值及方程f(x)=0在(a,b)内的实根个数时,如果f(x)的驻点及f′(x)的不存在的点的个数大于等于2,总是列出类似题解中所列的表,可快捷地获得结果.
本题的有关内容见提高篇05.
(19)分析 先按所给的等式建立关于函数f(x)的微分方程,然后求解微分方程得到f(x)的表达式.
精解 由于
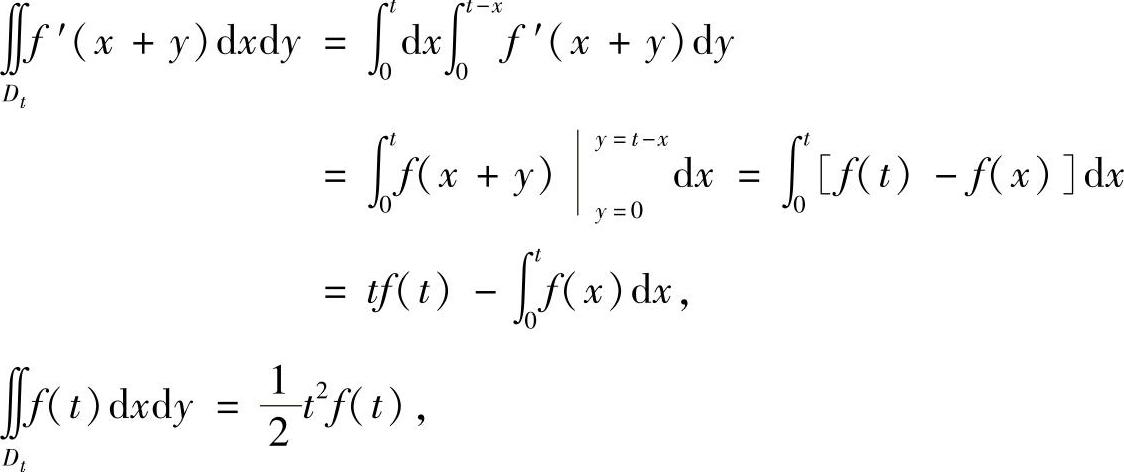
所以,由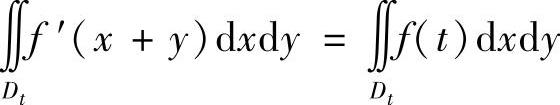
得 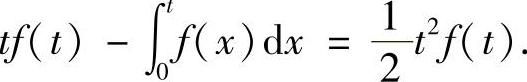
上式两边求导得
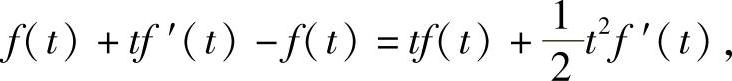
化简后成为
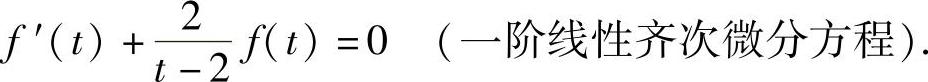
它的通解为
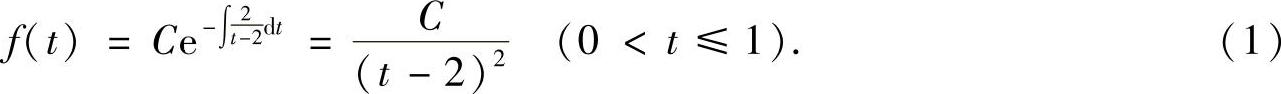
由于f(t)在[0,1]上连续,所以由

得C=4.将它代入式(1)得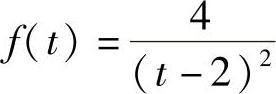 ,即
,即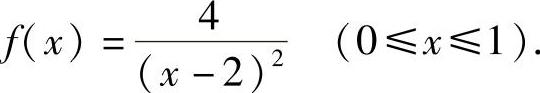
附注 注意题解中的微分方程是分两步才建立的:
(ⅰ)通过二重积分的计算建立方程
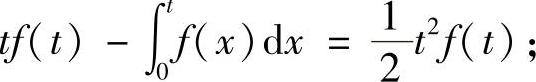
(ⅱ)通过求导将上述方程转换成微分方程.
本题是综合题,有关内容及计算方法见提高篇12,13.
(20)分析 可用矩阵方程快捷地解本题.
精解 (Ⅰ)由于α1,α2,α3不能由β1,β2,β3线性表示,所以矩阵方程
(β1,β2,β3)X=(α1,α2,α3)
无解(其中X是三阶未知矩阵),从而
r(β1,β2,β3)<r(β1,β2,β3┆α1,α2,α3).(1)
对增广矩阵(β1,β2,β3︙α1,α2,α3)施行初等行变换:

所以由式(1)得a=5.
(Ⅱ)为了确定β1,β2,β3关于α1,α2,α3的线性表示式,构造矩阵方程
(α1,α2,α3)Y=(β1,β2,β3)(其中Y是三阶未知矩阵).(2)
对式(2)的增广矩阵(α1,α2,α3︙β1,β2,β3)(将a=5代入)施行初等行变换:
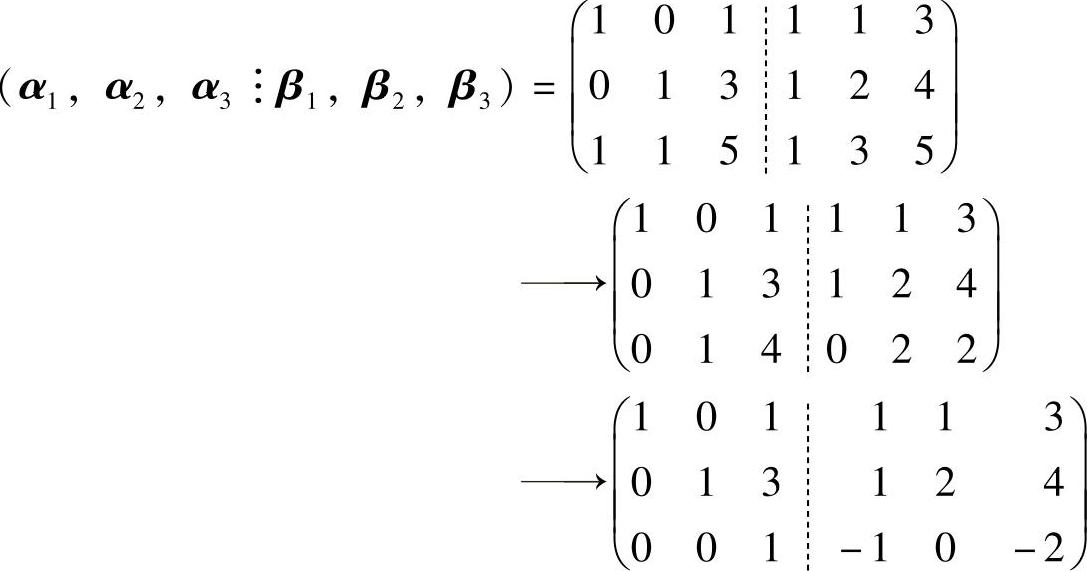
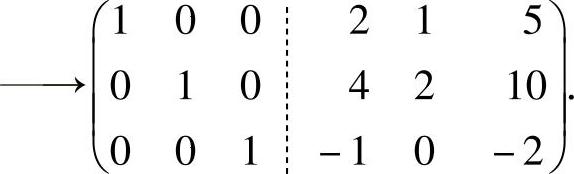
所以 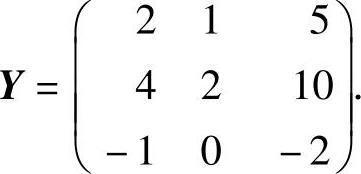
故 β1=2α1+4α2-α3,β2=α1+2α2,β3=5α1+10α2-2α3.
附注 求解矩阵方程是计算向量组之间线性表示式的有效方法.如果A是可逆矩阵,则矩阵方程AX=B可直接获解,即
X=A-1B.
对于本题的(α1,α2,α3)Y=(β1,β2,β3),由于
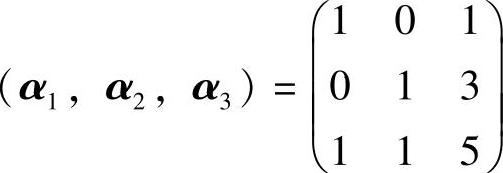
可逆,且其逆矩阵为 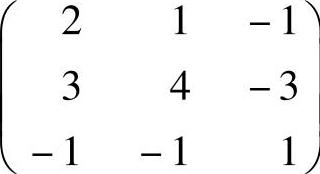 ,
,
所以

故 β1=2α1+4α2-α3,β2=α1+2α2,β3=5α1+10α2-2α3.
本题是综合题,其有关内容见提高篇18.
(21)分析 (Ⅰ)按所给条件,利用特征值与特征向量概念,计算矩阵A的特征值与特征向量.计算时要利用实对称矩阵对应不同特征值的特征向量正交的性质.
(Ⅱ)利用(Ⅰ)将矩阵A正交相似对角化,从而得到A.
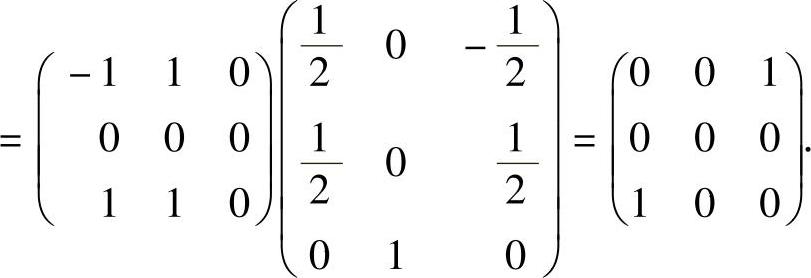
精解 (Ⅰ)由题设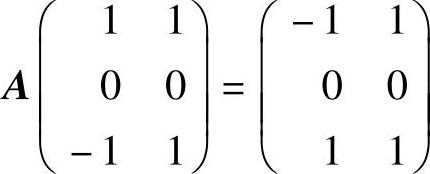 ,即
,即
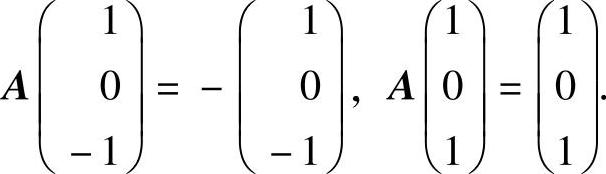
由此知,矩阵A有特征值λ=-1,1,对应的特征向量分别为C1(1,0,-1)T,C2(1,0,1)T(其中C1,C2是任意非零常数).
由于r(A)=2,所以矩阵A的第三个特征值为λ=0,记它对应的特征向量为(x1,x2,x3)T,则它与(1,0,-1)T,(1,0,1)T都正交,即满足:
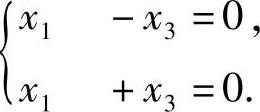
该三元方程组的基础解系为(0,1,0)T,所以λ=0对应的特征向量为C3(0,1,0)T(其中C3是任意非零常数).
(Ⅱ)由于矩阵A的对应特征值λ=-1,1,0的特征向量(1,0,-1)T,(1,0,1)T和(0,1,0)T两两正交,现将它们单位化得
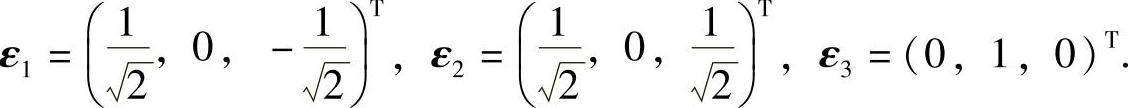
记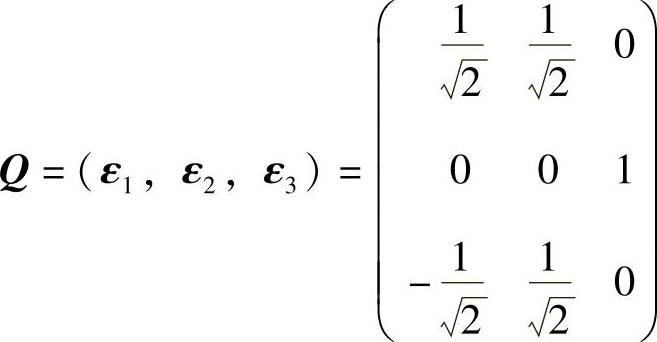 (正交矩阵),则
(正交矩阵),则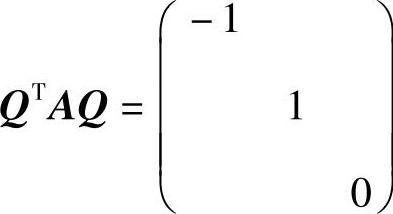 ,
,
所以

附注 在第(Ⅱ)小题中也可以由A的对应特征值λ=-1,1,0的三个特征向量为列向量构成矩阵P,即记
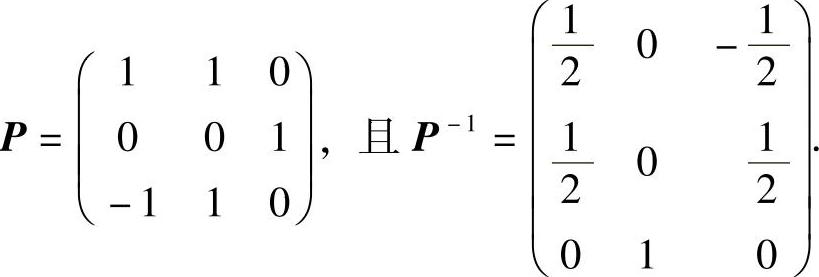
于是由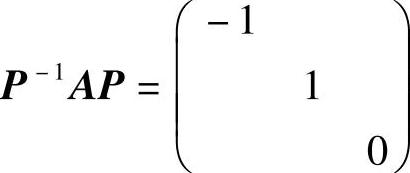 得
得
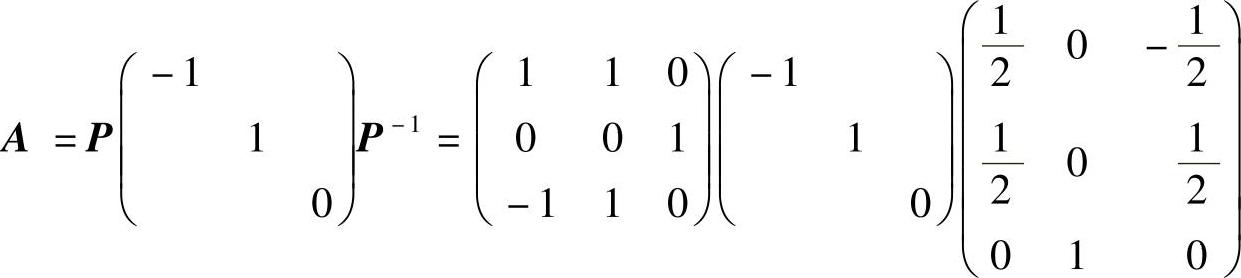
(22)分析 (Ⅰ)利用题设P(X2=Y2)=1,即P(X=0,Y=-1)=P(X=0,Y=1)=P(X=1,Y=0)=0及所给的(X,Y)的边缘概率分布,计算二维随机变量(X,Y)的概率分布.
(Ⅱ)利用(Ⅰ)中算得的(X,Y)的概率分布,计算随机变量Z的概率分布.
(Ⅲ)利用二维随机变量(X,Y)的概率分布和ρXY的计算公式计算ρXY.
精解 (Ⅰ)由P(X2=Y2)=1及X与Y的概率分布知(X,Y)的概率分布及边缘概率分布应如下表所示:
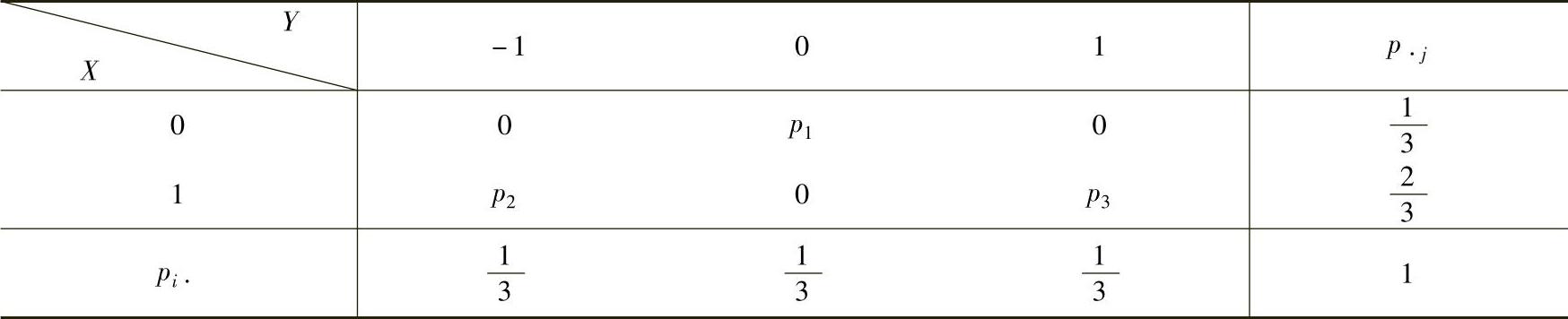
由表可知,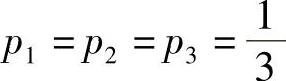 ,所以(X,Y)的概率分布为
,所以(X,Y)的概率分布为

(Ⅱ)Z可能取的值有-1,0,1,且
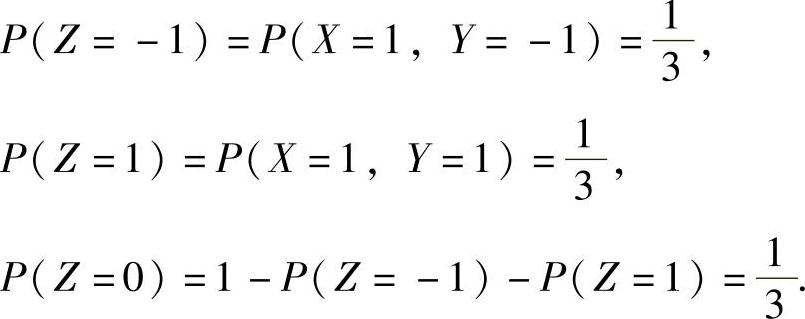
因此Z的概率分布可如下表所示:

(Ⅲ)由于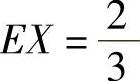 ,
,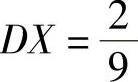 ;EY=0,
;EY=0,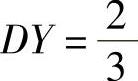 ,所以由
,所以由
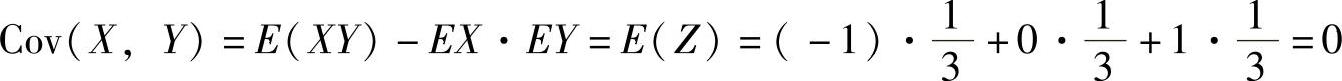
得
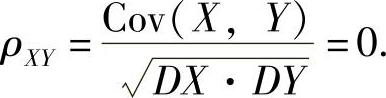
附注 本题表明虽然X与Y不相关,但X与Y不独立.
通常,当具有正方差的随机变量X与Y相互独立时,必不相关;但反之未必正确.当(X,Y)服从二维正态分布时,X与Y相互独立的充分必要条件为X与Y不相关.
本题是综合题.有关内容及计算方法见提高篇21,24.
(23)分析 先画出区域G的图形和写出二维随机变量(X,Y)的概率密度,然后按边缘概率密度与条件概率密度公式计算fX(x)与fX|Y(x|y).
精解 区域G如图B.11.1阴影部分所示,因此(X,Y)的概率密度为
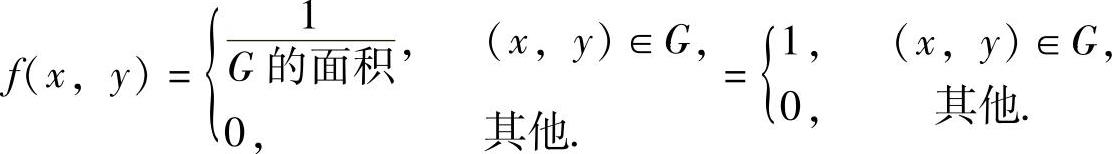
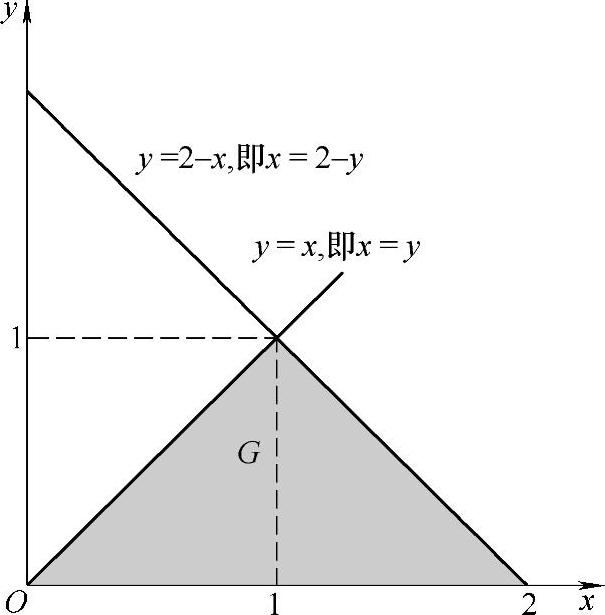
图 B.11.1

(Ⅱ)为计算fX|Y(x|y),先计算fY(y):
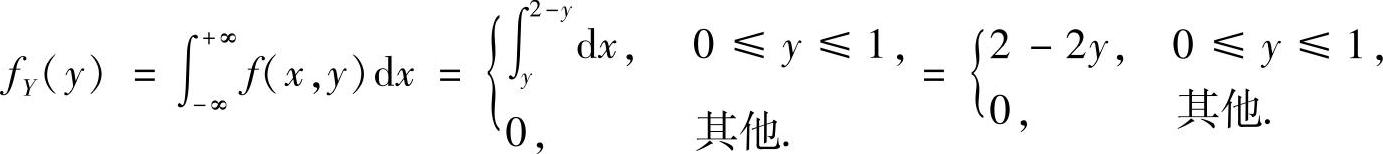
显然,仅在[0,1)上fY(y)≠0,所以对任意y∈[0,1),

附注 对于任意固定的y∈[0,1),f(x,y)成为x的函数,它定义在如图B.11.2所示的与x轴平行的直线l上,l位于G内部的区间为[y,2-y],所以对任意固定的y∈[0,1),有
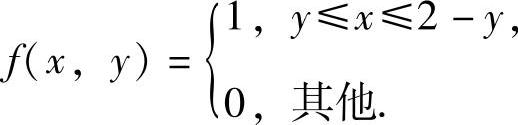
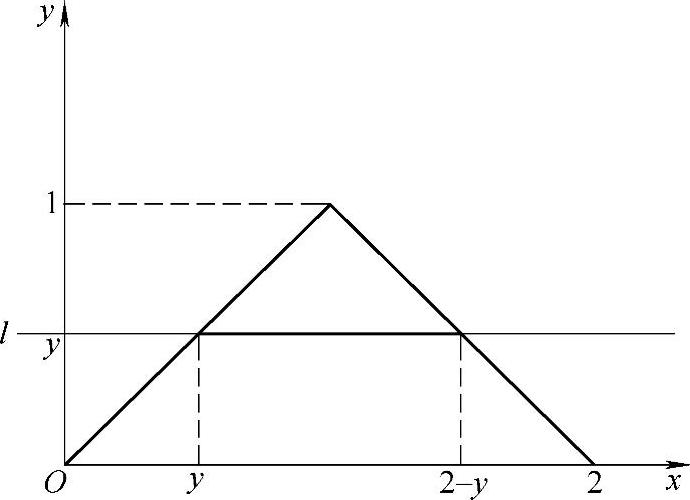
图 B.11.2
