2012年全国硕士研究生入学统一考试试题精解
一、选择题
(1)分析 分别确定曲线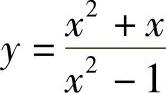 的铅垂和非铅垂渐近线的系数即可.
的铅垂和非铅垂渐近线的系数即可.
精解 y在点x=-1,1处无定义,但
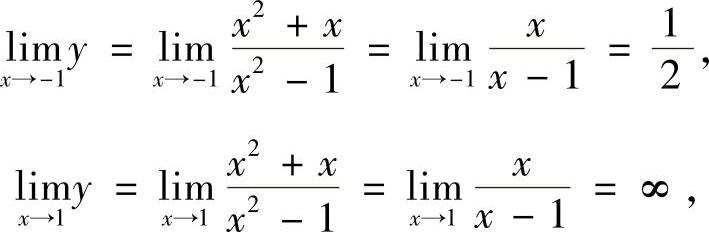
所以,所给曲线只有一条铅垂渐近线x=1.此外,由
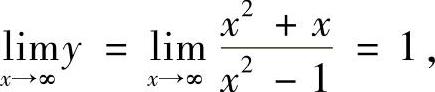
所以,所给曲线只有一条非铅垂渐近线y=1(它为水平渐近线).
因此本题选(C).
附注 在计算曲线y=f(x)的非铅垂渐近线时,如果
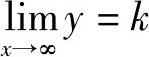 ,则必有非铅垂渐近线(水平渐近线)y=k(当以上的极限不存在时,应考虑x→+∞与x→-∞的极限).
,则必有非铅垂渐近线(水平渐近线)y=k(当以上的极限不存在时,应考虑x→+∞与x→-∞的极限).
(2)分析 按导数定义计算f′(0).
精解 由于f(0)=0,所以
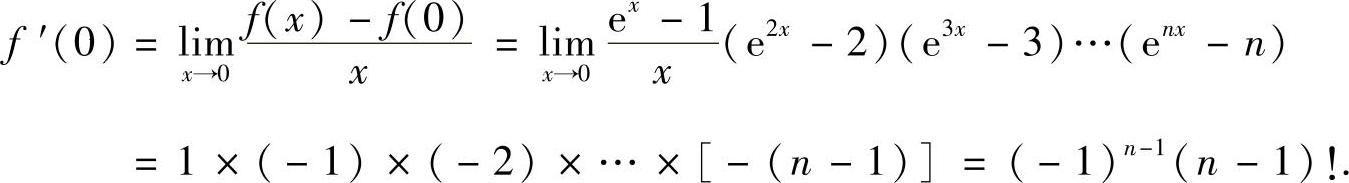
因此本题选(A).
附注 用以下方法也可计算f′(0):
由于
f′(x)={(ex-1)[(e2x-2)(e3x-3)…(enx-n)]}′
=ex(e2x-2)(e3x-3)…(enx-n)+(ex-1)[(e2x-2)…(enx-n)]′,
所以,
f′(0)=1×(-1)×(-2)×…×[-(n-1)]+0×[(e2x-2)…(enx-1)]′x=0
=(-1)n-1(n-1)!.
(3)分析 确定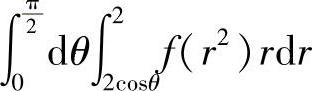 对应的二重积分的积分区域D,即可判定正确选项.
对应的二重积分的积分区域D,即可判定正确选项.
精解 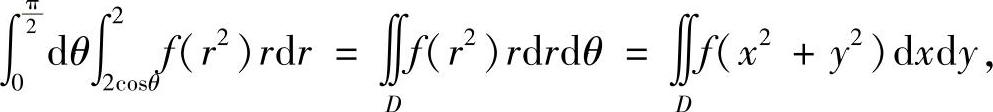
其中D={(x,y)0≤x≤2,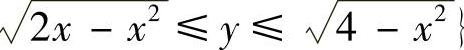 ,如图B.12.1阴影部分所示,所以
,如图B.12.1阴影部分所示,所以
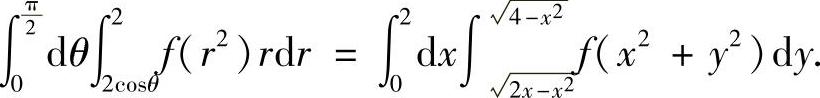
因此本题选(B).
附注 要将极坐标系下的二次积分转换成直角坐标系下的二次积分,首先应画出对应的二重积分的积分区域D,并且写出它在直角坐标系中的表达式.
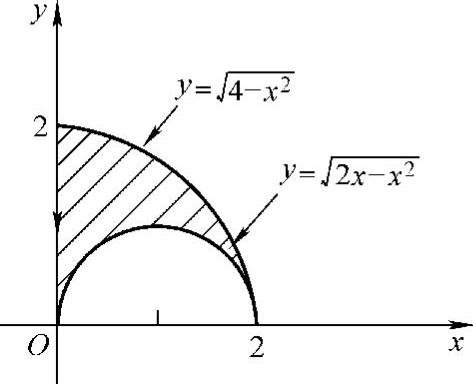
图 B.12.1
(4)分析 利用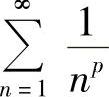 收敛时p>1,
收敛时p>1,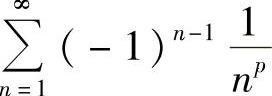 条件收敛时0<p≤1,确定题中α的取值范围.
条件收敛时0<p≤1,确定题中α的取值范围.
精解 由于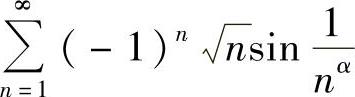 绝对收敛,即
绝对收敛,即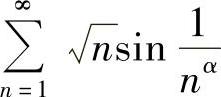 收敛,或
收敛,或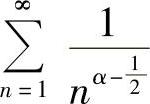 收敛,所以
收敛,所以
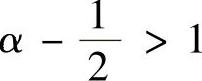 ,即
,即
由于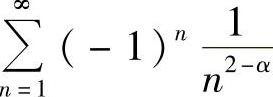 条件收敛,所以
条件收敛,所以
0<2-α≤1,即1≤α<2. (2)
由式(1)、式(2)得 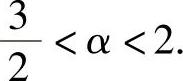
因此本题选(D).
附注 应记住以下结论:(ⅰ) 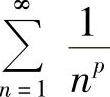 (p级数)收敛的充分必要条件是p>1.(ⅱ)
(p级数)收敛的充分必要条件是p>1.(ⅱ) 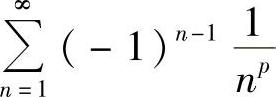 绝对收敛的充分必要条件是p>1,条件收敛的充分必要条件是0<p≤1.
绝对收敛的充分必要条件是p>1,条件收敛的充分必要条件是0<p≤1.
(5)分析 只要在α1,α2,α3,α4中找到三个向量,以它们为列的矩阵的行列式为零即可.
精解 由于
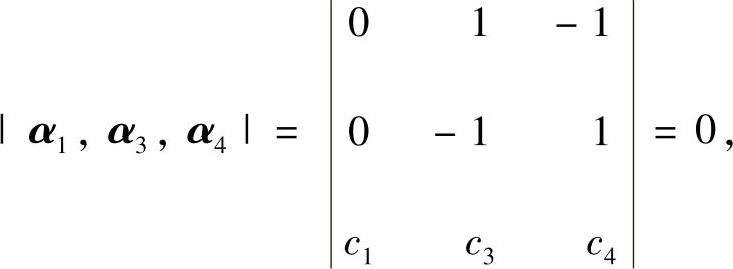
所以,向量组α1,α3,α4线性相关.
因此本题选(C).
附注 判别n个n维列向量组α1,α2,…,αn的线性相关性的快捷方法是,构造矩阵
A=(α1,α2,…,αn),
当|A|=0时,α1,α2,…,αn线性相关;
当|A|≠0时,α1,α2,…,αn线性无关.
(6)分析 利用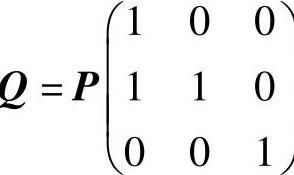 即可算出Q-1AQ.
即可算出Q-1AQ.
精解 由于
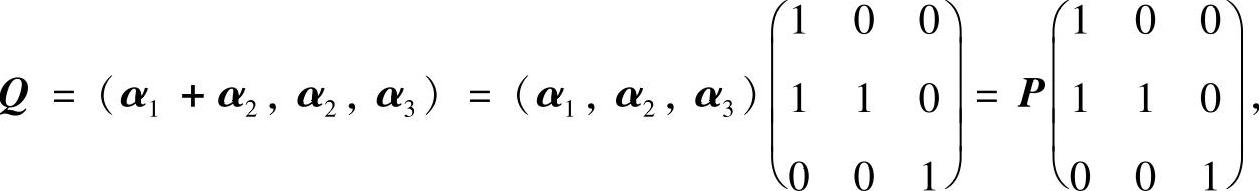
所以,
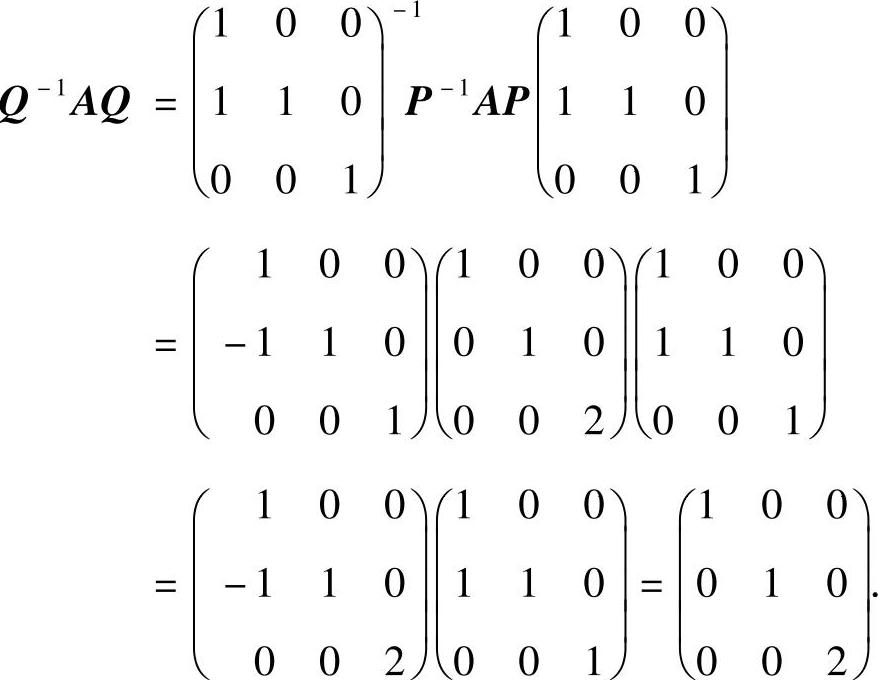
因此本题选(B).
附注 本题也可用以下方法快捷计算:
由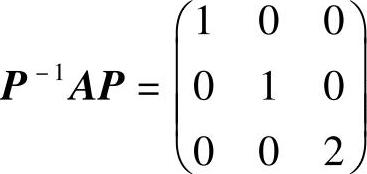 知,α1,α2是A的对应特征值λ=1的两个线性无关的特征向量,所以α1+α2,α2也是A的对应特征值λ=1的两个线性无关的特征向量,因此对于Q=(α1+α2,α2,α3)有
知,α1,α2是A的对应特征值λ=1的两个线性无关的特征向量,所以α1+α2,α2也是A的对应特征值λ=1的两个线性无关的特征向量,因此对于Q=(α1+α2,α2,α3)有
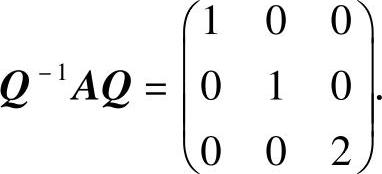
(7)分析 先写出(X,Y)的概率密度,然后计算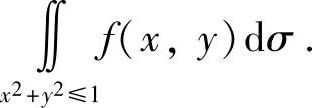
精解 记D1={(x,y)|0<x<1,0<y<1},
D2={(x,y)|x2+y2≤1},
则二维随机变量(X,Y)的概率密度为
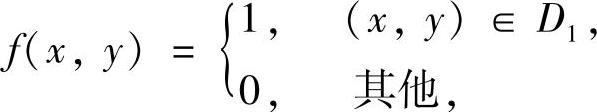
于是,
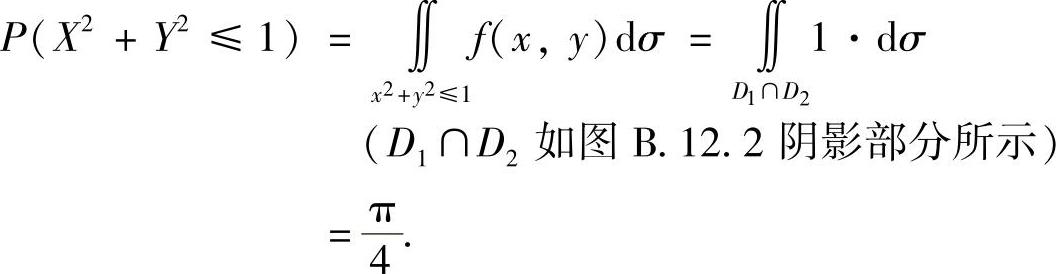
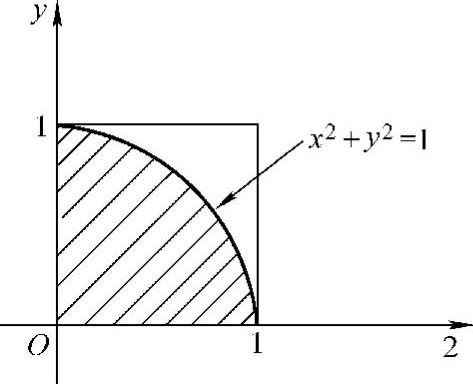
图 B.12.2
因此本题选(D).
附注 X与Y的概率密度分别为
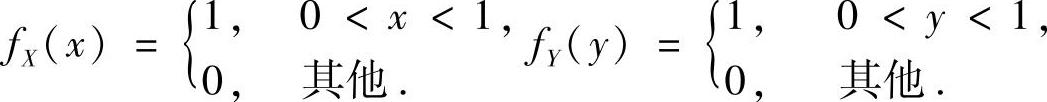
由于X与Y相互独立,所以(X,Y)的概率密度为
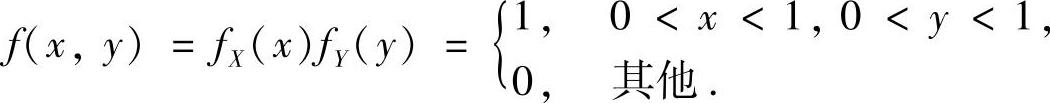
(8)分析 先确定X1-X2与X3-X4的分布,然后按抽样分布的定义确定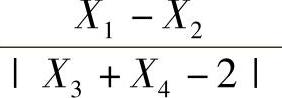 的分布.
的分布.
精解 由题设知X1-X2~N(0,2σ2),所以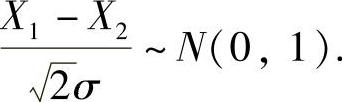
同样由题设知X3+X4-2~N(0,2σ2),所以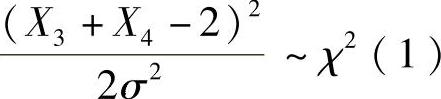 .而且
.而且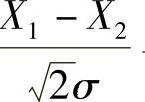 与
与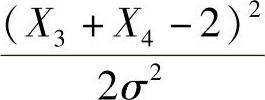 相互独立,
相互独立,
所以 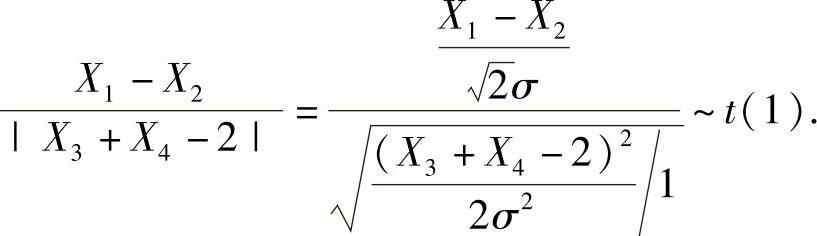
因此本题选(B).
附注 要记住常用的三个抽样分布χ2(n),t(n)及F(n1,n2)的定义.
二、填空题
(9)分析 所给极限是1∞型未定式极限,所以将函数指数化后计算.
精解 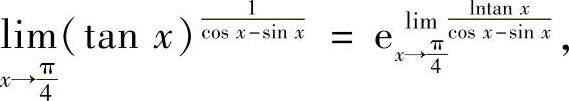
其中 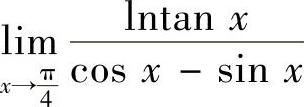 (
(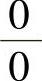 型未定式极限)
型未定式极限)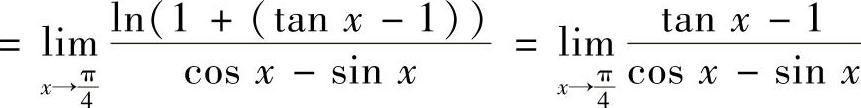
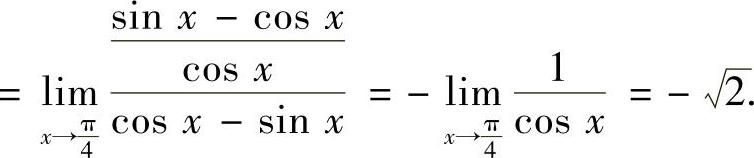
所以, 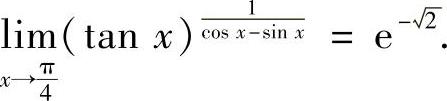
附注 极限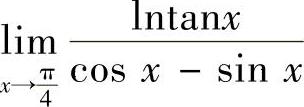 也可用洛必达法则计算,具体如下:
也可用洛必达法则计算,具体如下:

(10)分析 先写出y=f(f(x))在点x=e的小邻域内的表达式,然后计算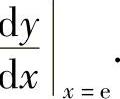
精解 记u=f(x),则y=f(f(x))=f(u).
当x位于点x=e的某个小邻域内时,u应按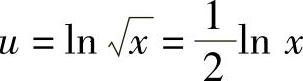 计算,它位于
计算,它位于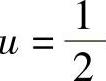 的某个小邻域内,此时y应按2u-1计算.所以在点x=e的某个小邻域内,有
的某个小邻域内,此时y应按2u-1计算.所以在点x=e的某个小邻域内,有
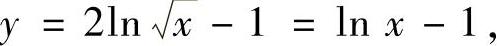
因此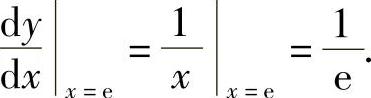
附注 题解中只需写出y=f(f(x))的局部表达式,它在(-∞,+∞)上的表达式具体计算如下:
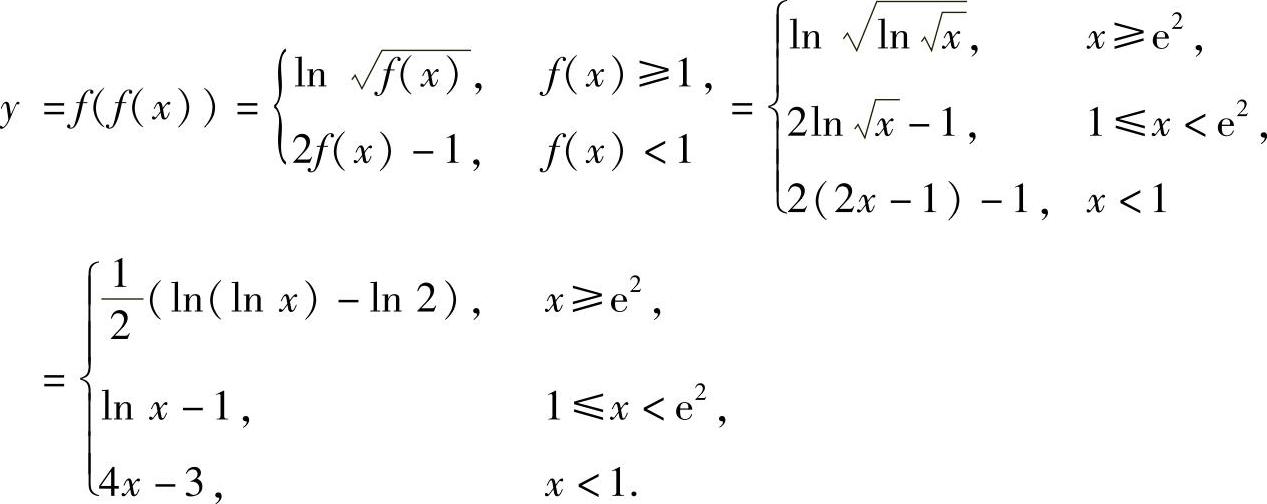
(11)分析 按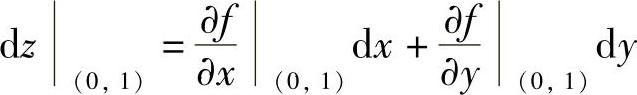 计算,所以只要算出
计算,所以只要算出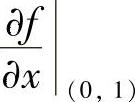 与
与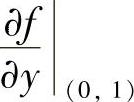 即可.
即可.
精解 由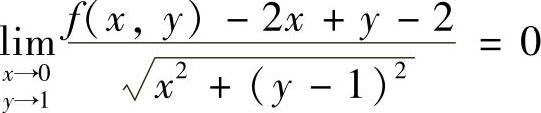 知,x→0,y→1时有
知,x→0,y→1时有
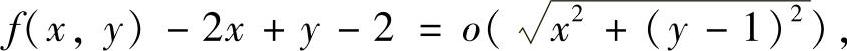
即 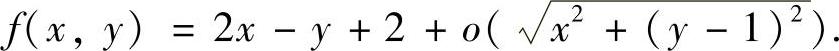
再由f(x,y)连续得
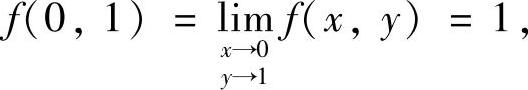
所以
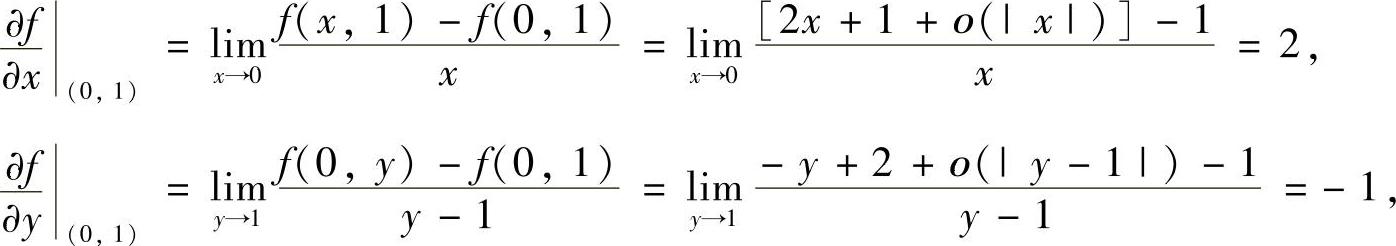
从而
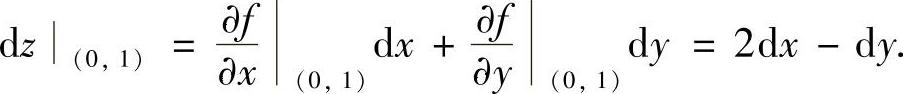
附注 实际上dz(0,1)可按全微分定义直接得到,具体如下:
由题中所给极限可得
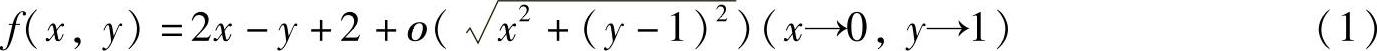
以及由f(x,y)连续得f(0,1)=1.于是式(1)可以改写成
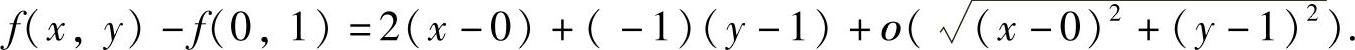
因此由全微定义知
dz|(0,1)=2dx-dy.
(12)分析 画出题中平面图形的概图,然后由定积分计算它的面积.
精解 记D为由曲线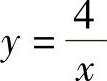 和直线y=x及y=4x在第一象限中围成的平面图形,如图B.12.3阴影部分所示.
和直线y=x及y=4x在第一象限中围成的平面图形,如图B.12.3阴影部分所示.
用直线x=1将D划分成D1与D2两部分,如图B.12.3所示.显然
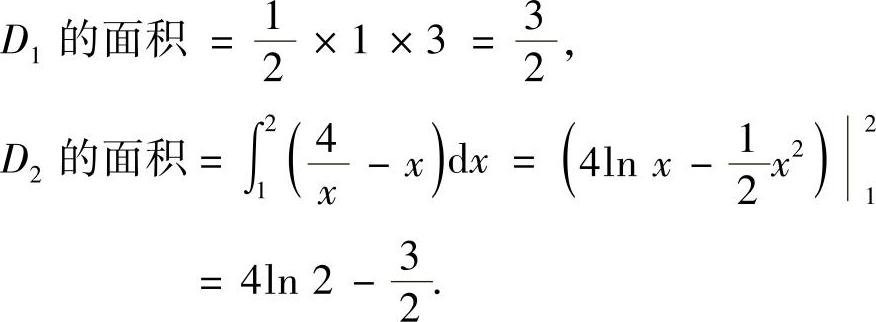
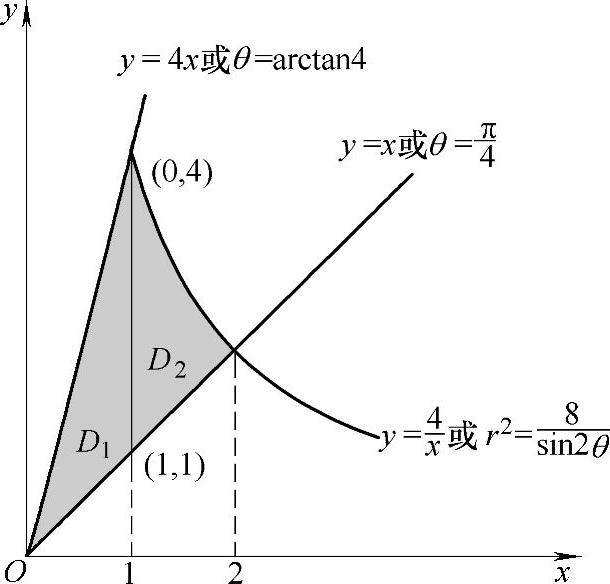
图 B.12.3
所以

附注 由于D是角域的一部分,所以它的面积也可以用极坐标计算,具体如下:
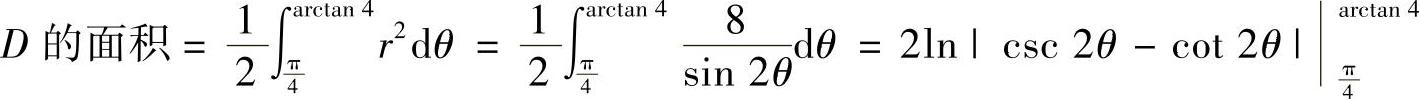
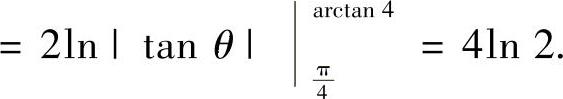
(13)分析 利用公式AA∗=|A|E3(其中E3是三阶单位矩阵),并用初等矩阵与A之积表示B,即可算出|BA∗|.
精解 由题设得
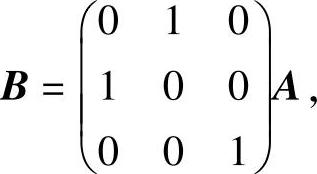
所以
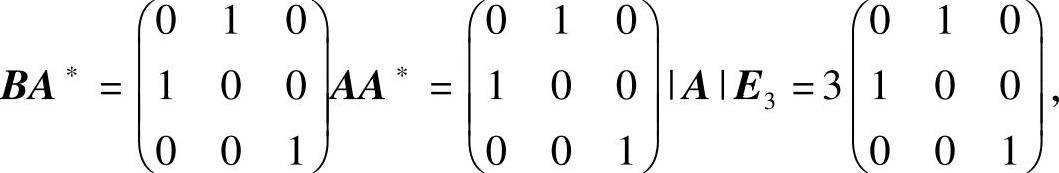
所以

附注 应记住:当A是n阶矩阵时,
AA∗=A∗A=|A|En(En是n阶单位矩阵,A∗是A的伴随矩阵).
并应熟练掌握矩阵M的每一个初等行变换(初等列变换)都对应一个初等矩阵,并且对M左乘(右乘)这个初等矩阵即为M经此初等行变换(初等列变换)后的矩阵.
(14)分析 利用条件概率计算公式计算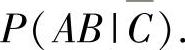
精解 
附注 题解中利用了多个概率计算公式,其中特别是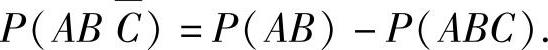
这个等式可推导如下: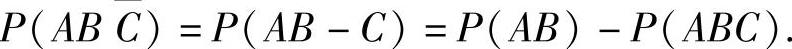
三、解答题
(15)分析 所给极限是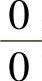 型未定式,化简后用洛必达法则计算.
型未定式,化简后用洛必达法则计算.
精解 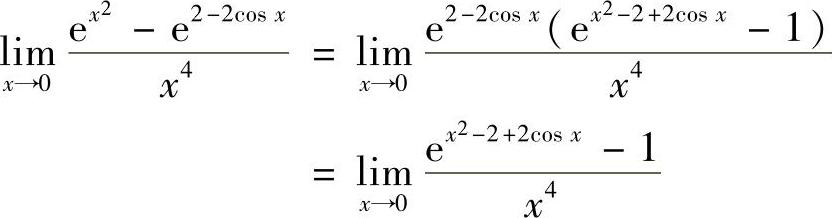

附注 如果用带佩亚诺型余项的麦克劳林公式,则可快捷算得极限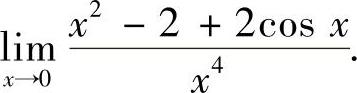
具体如下:
由于x→0时,
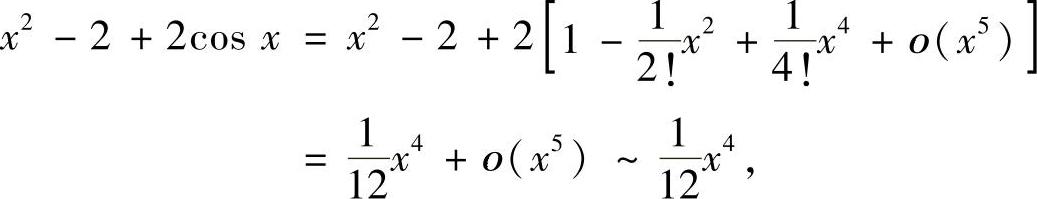
所以
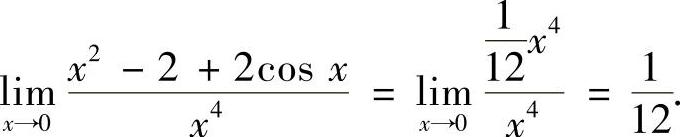
本题的有关内容及计算方法见提高篇01.
(16)分析 画出D的概图,然后按“先y后x”顺序计算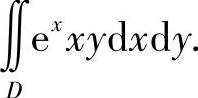
精解 区域D如图B.12.4阴影部分所示,则
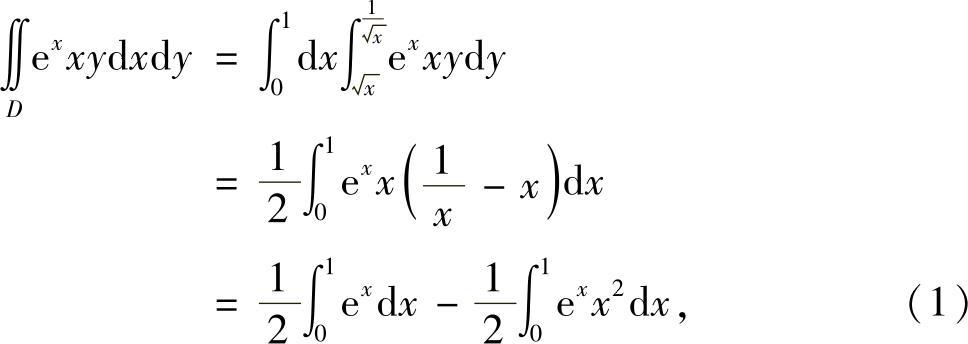
其中,
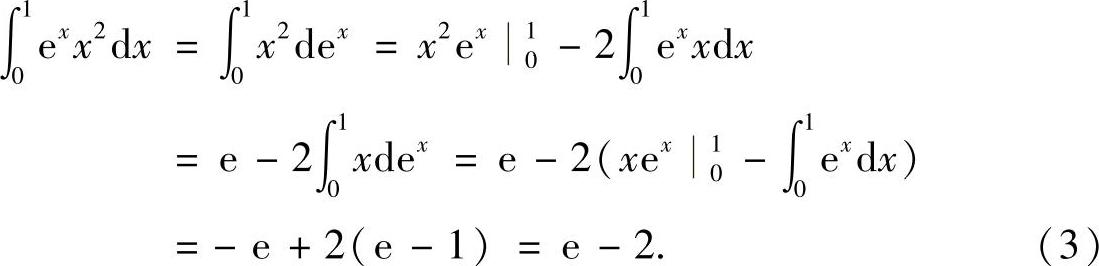
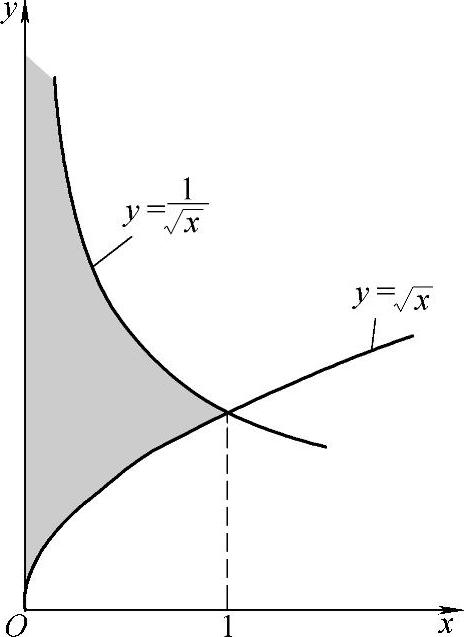
图 B.12.4
将式(2)、式(3)代入式(1)得
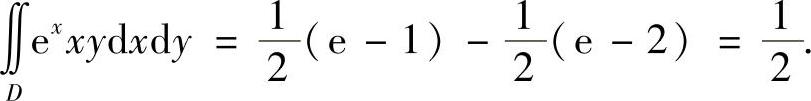
附注 本题按“先y后x”顺序计算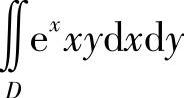 比较快捷,如果按“先x后y”顺序计算,则需用直线y=1将D分成两部分,并在各部分上按“先x后y”顺序计算
比较快捷,如果按“先x后y”顺序计算,则需用直线y=1将D分成两部分,并在各部分上按“先x后y”顺序计算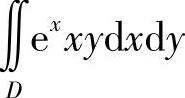 ,计算量较大.
,计算量较大.
本题是无界区域上的二重积分,其计算方法与有界闭区域上的二重积分相同,即将二重积分转换成二次积分.(https://www.daowen.com)
(17)分析 (Ⅰ)由题设知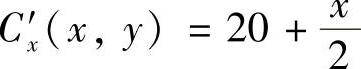 ,Cy′ (x,y)=6+y及C(0,0)=10000,由此即可算出C(x,y).
,Cy′ (x,y)=6+y及C(0,0)=10000,由此即可算出C(x,y).
(Ⅱ)利用拉格朗日乘数法计算C(x,y)在约束条件x+y=50下的最小值点与最小值.
(Ⅲ)在(Ⅱ)中算得的x,y值后,计算Cx′(x,y),并对此作出经济学上的解释.
精解 由题设知

Cy′(x,y)=6+y, (2)
C(0,0)=10000. (3)
由式(1)得
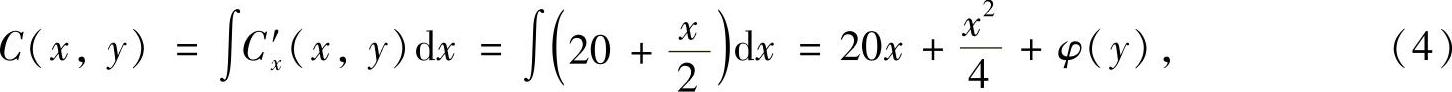
式(4)的两边对y求偏导数得
Cy′ (x,y)=φ′(y).
将其与式(2)比较得
φ′(y)=6+y,即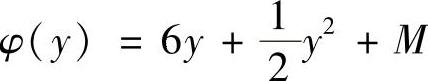 (M是常数). (5)
(M是常数). (5)
将式(5)代入式(4)得
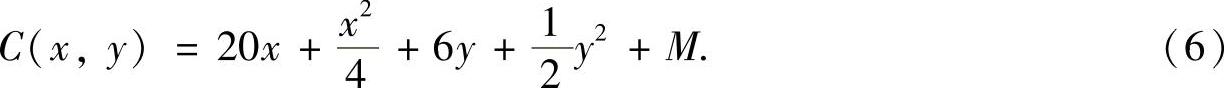
将式(3)代入式(6)得M=10000,所以
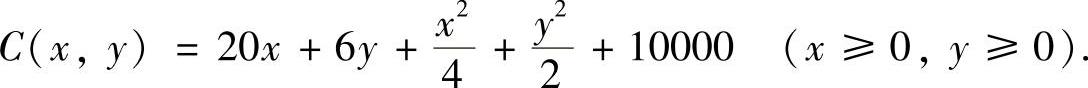
(Ⅱ)为计算在约束条件x+y=50下C(x,y)的最小值,作拉格朗日函数
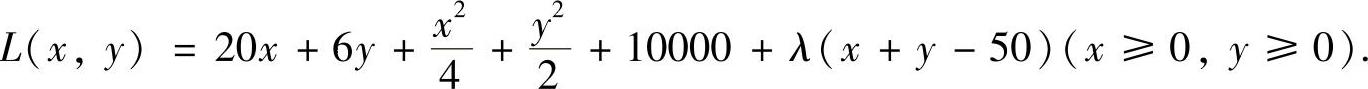
令 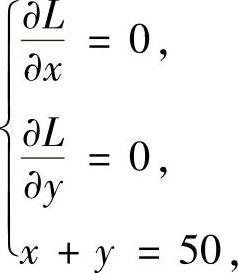 即
即 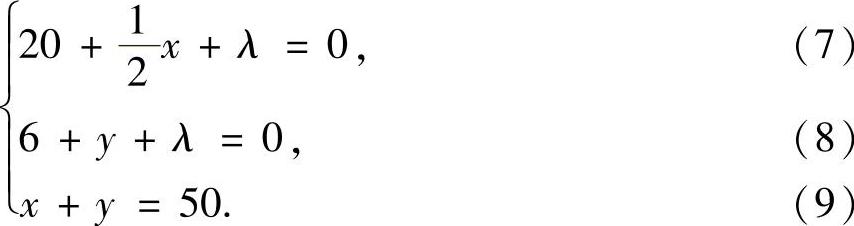
式(7)-式(8)并与式(9)联立得
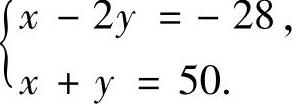
解此方程组得唯一解 x=24,y=26.
所以由题设知,在约束条件x+y=50下,C(x,y)在x=24、y=26处取得最小值,即甲、乙两种产品的产量分别为24件与26件时,总成本最小。最小总成本为C(24,26)=11118(万元).
(Ⅲ)由(Ⅱ)知,总成本最小时,甲产品的边际成本为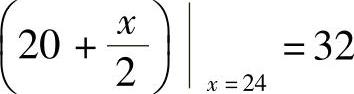 万元/件,在经济学上,它表示在甲、乙两种产品的产量分别为24件与26件时,甲产品的产量每增加一件时,总成本将增加32万元.
万元/件,在经济学上,它表示在甲、乙两种产品的产量分别为24件与26件时,甲产品的产量每增加一件时,总成本将增加32万元.
附注 应理解经济学中“边际”“弹性”等概念.
(18)分析 由于
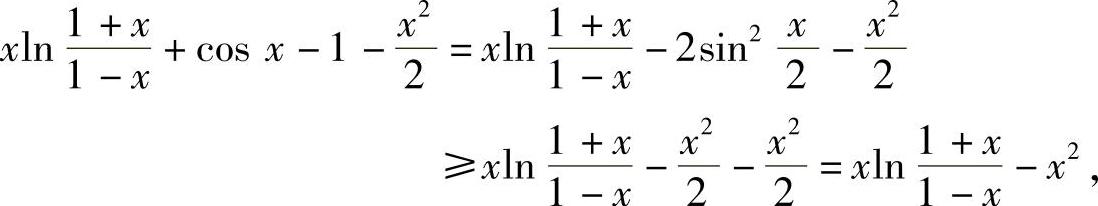
所以只要证明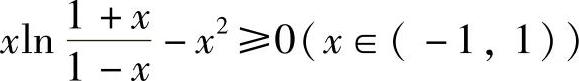 即可.
即可.
精解 当x∈[0,1)时,有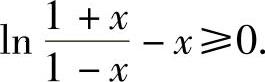 为证明这一不等式作辅助函数
为证明这一不等式作辅助函数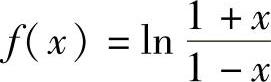
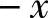 ,则f(x)在[0,1)上连续,在(0,1)内可导且
,则f(x)在[0,1)上连续,在(0,1)内可导且
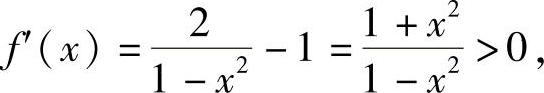
所以,在[0,1)上f(x)≥f(0),即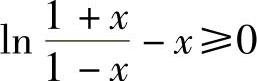 ,从而
,从而
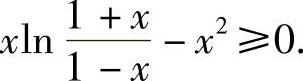
由此推得
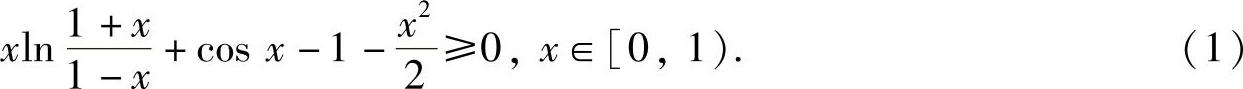
由于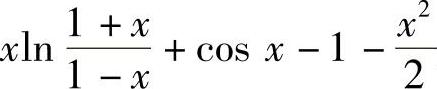 是偶函数,所以式(1)在(-1,0]上也成立,因此得证
是偶函数,所以式(1)在(-1,0]上也成立,因此得证
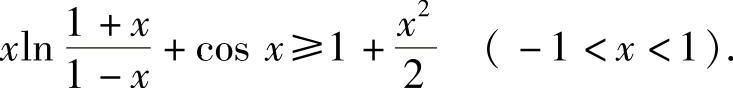
附注 不先化简而直接证明题中不等式是不容易的,故对它作两次化简.
(ⅰ)将欲证的不等式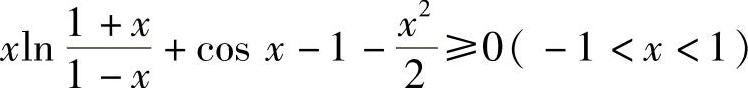 左边函数缩小成
左边函数缩小成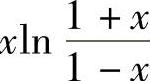
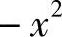 .故只要证明
.故只要证明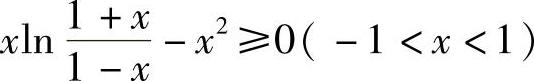 即可.
即可.
(ⅱ)将x限制在[0,1)上,则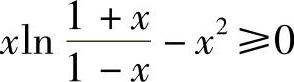 又可进一步化简为
又可进一步化简为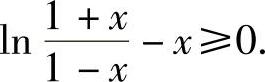
本题的有关内容及证明方法见提高篇05.
(19)分析 (Ⅰ)从求解二阶常系数齐次线性微分方程f″(x)+f′(x)-2f(x)=0入手计算f(x)的表达式.
(Ⅱ)将(Ⅰ)中算得的f(x)代入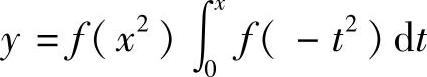 ,计算y″,由此得到曲线
,计算y″,由此得到曲线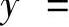
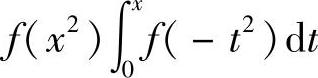 的拐点.
的拐点.
精解 (Ⅰ)f″(x)+f′(x)-2f(x)=0是二阶常系数齐次线性微分方程,它的特征方程r2+r-2=0有根r=1,-2,所以通解为
f(x)=C1ex+C2e-2x. (1)
将式(1)代入f″(x)+f(x)=2ex得
2C1ex+5C2e-2x=2ex,
所以,C1=1,C2=0.将它们代入式(1)得f(x)=ex.
(Ⅱ)由(Ⅰ)得
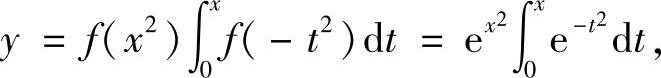
所以
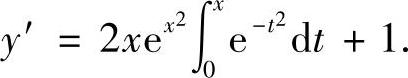
于是由
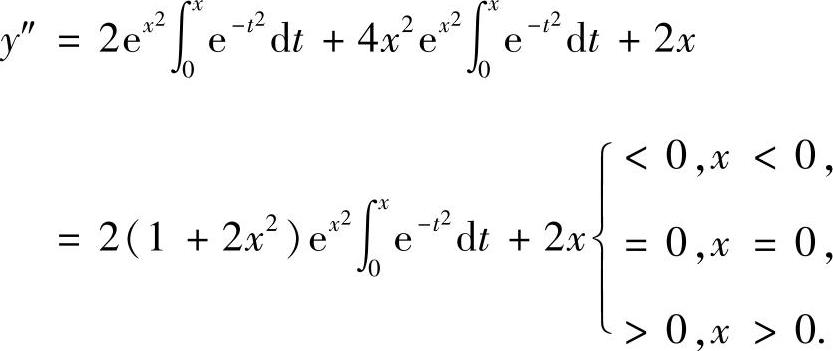
知,(0,y(0))=(0,0)是曲线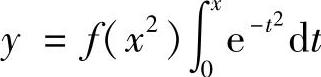 的唯一拐点.
的唯一拐点.
附注 本题也可以按以下方法计算f(x)的表达式:
由f″(x)+f(x)=2ex得f″(x)=2ex-f(x).将它代入f″(x)+f′(x)-2f(x)=0得
f′(x)-3f(x)=-2ex (一阶线性微分方程),它的通解为 f(x)=e3x(C+e-2x)=Ce3x+ex. (2)
将式(2)代入f″(x)+f(x)=2ex得C=0.再将C=0代入式(2)得f(x)=ex.
本题是综合题,有关内容及计算方法见提高篇05,14.
(20)分析 (Ⅰ)按第一行展开计算行列式|A|.
(Ⅱ)令A=0,算出的a值中,能使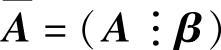 与A有相等秩的a值即为所求.然后计算对应的方程组Ax=β的通解.
与A有相等秩的a值即为所求.然后计算对应的方程组Ax=β的通解.
精解 (Ⅰ)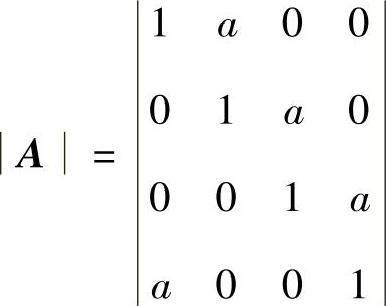
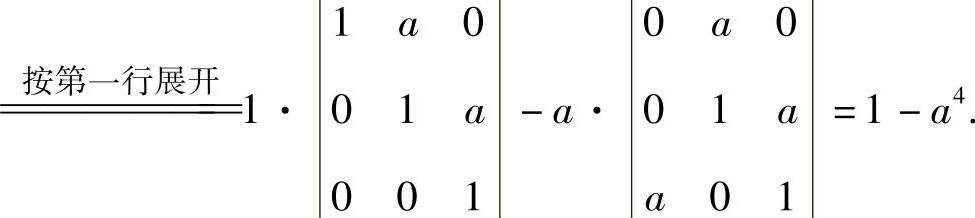
(Ⅱ)由A=0,即1-a4=0得a=1,-1.
当a=1时,对方程组Ax=β的增广矩阵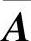 施行初等行变换:
施行初等行变换:

由此可知,此时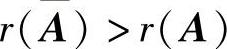 .所以a=1不是所求的.
.所以a=1不是所求的.
当a=-1时,对方程组Ax=β的增广矩阵A施行初等行变换.
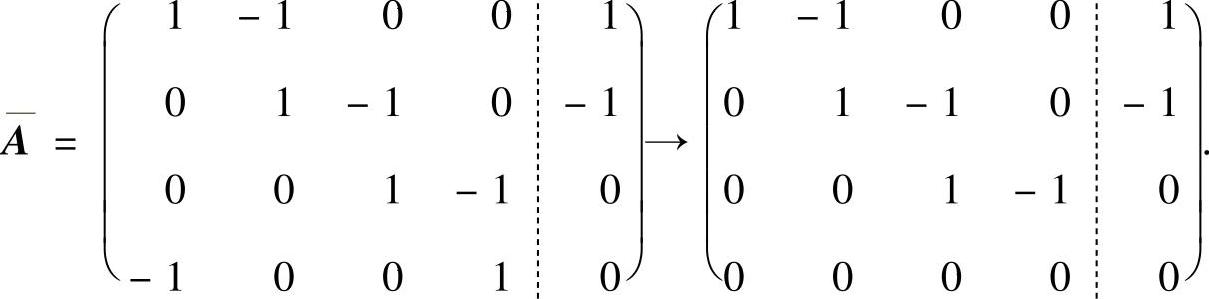
由此可知,此时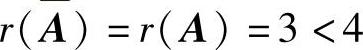 ,方程组Ax=β有无穷多解.因此所求的a=-1.由于此时方程组Ax=β与方程组
,方程组Ax=β有无穷多解.因此所求的a=-1.由于此时方程组Ax=β与方程组

同解.方程组(1)的导出组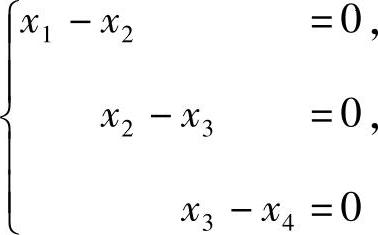 的通解为C(1,1,1,1)T,此外,方程组(1)
的通解为C(1,1,1,1)T,此外,方程组(1)
有特解(0,-1,0,0)T,所以当a=-1时,方程组Ax=β的通解为
x=(x1,x2,x3,x4)T=C(1,1,1,1)T+(0,-1,0,0)T(其中C为任意常数).
附注 题解中值得注意的是:方程A=0的根未必都能使方程组Ax=β有无穷多解,需对方程|A|=0的根作一一检验;检验它们是否满足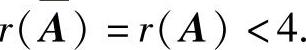
本题的有关内容与计算方法见提高篇18.
(21)分析 (Ⅰ)由ATA=0算出a的值.
(Ⅱ)对(Ⅰ)中算出的a,将对称矩阵ATA正交相似化,即QT(ATA)Q=Λ(对角矩阵),由此得到正交变换x=Qy及f的标准形.
精解 (Ⅰ)由于
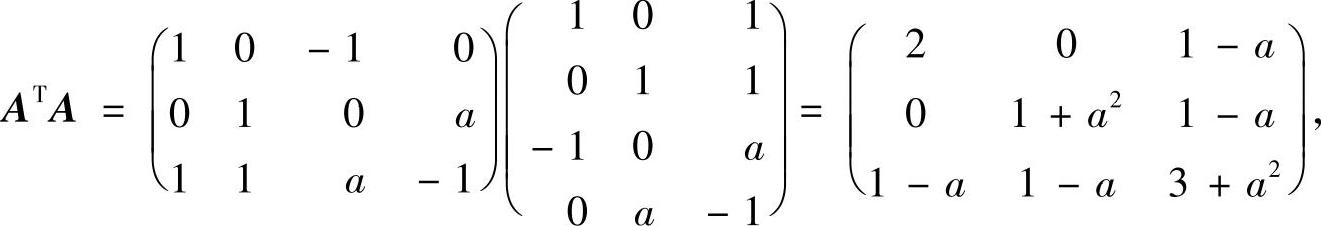
所以
|ATA|=2(1+a2)(3+a2)-(1-a)2(1+a2)-2(1-a)2
=2(1+a2)(3+a2)-(1-a)2(3+a2)
=(1+a)2(3+a2).
于是,由f(x1,x2,x3)的秩为2,即ATA的秩为2得|ATA|=0,即
(1+a)2(3+a2)=0.
由此得到a=-1(容易检验,当a=-1时,r(ATA)=2).
(Ⅱ)当a=-1时,
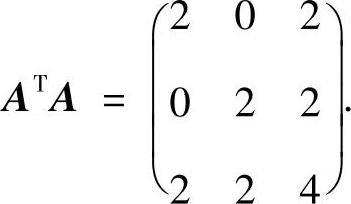
记E3为三阶单位矩阵,则由

得ATA的特征值为λ=0,2,6.
设对应λ=0的特征向量为α=(a1,a2,a3)T,则α满足:
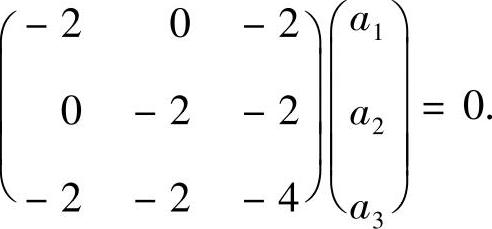
显然该方程组有解α=(-1,-1,1)T.
设对应λ=2的特征向量为β=(b1,b2,b3)T,则β满足:
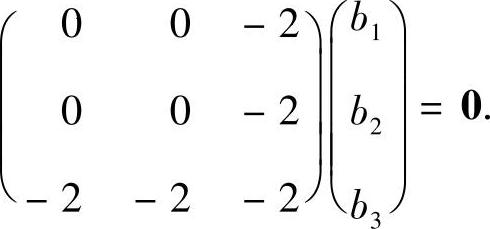
显然该方程组有解β=(-1,1,0)T.
设对应λ=6的特征向量为γ=(c1,c2,c3)T,则γ应与α,β正交,故有
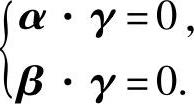 即
即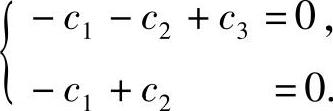
显然该方程组有解γ=(1,1,2)T.
由于α,β,γ两两正交,现将它们单位化:
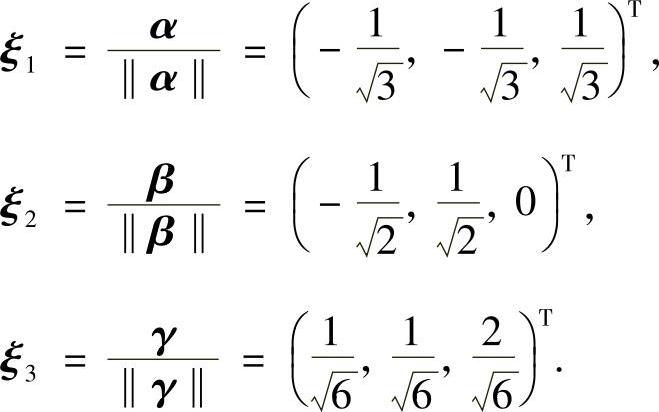
记Q=(ξ1,ξ2,ξ3),则Q是正交矩阵,且正交变换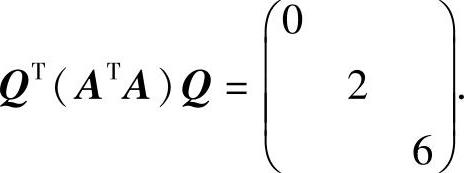 于是正交变换x=Qy(其中y=(y1,y2,y3)T)使得
于是正交变换x=Qy(其中y=(y1,y2,y3)T)使得
f=2y22+6y23(标准形).
附注 要熟练掌握用正交变换化二次型为标准形的方法,有关内容及计算方法见提高篇20.
(22)分析 (Ⅰ)由{X=2Y}={X=0,Y=0}∪{X=2,Y=1}可以得到P(X=2Y).
(Ⅱ)由于Cov(X-Y,Y)=Cov(X,Y)-DY,所以只要算出Cov(X,Y)与DY即可.
精解 (Ⅰ)由于{X=2Y}={X=0,Y=0}∪{X=2,Y=1},且{X=0,Y=0}与{X=2,Y=1}互不相容,所以
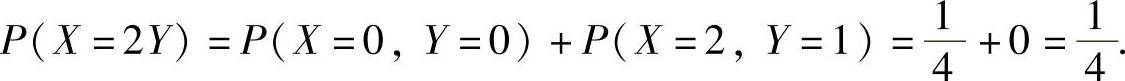
(Ⅱ)Cov(X-Y,Y)=Cov(X,Y)-Cov(Y,Y)=Cov(X,Y)-DY,(1)其中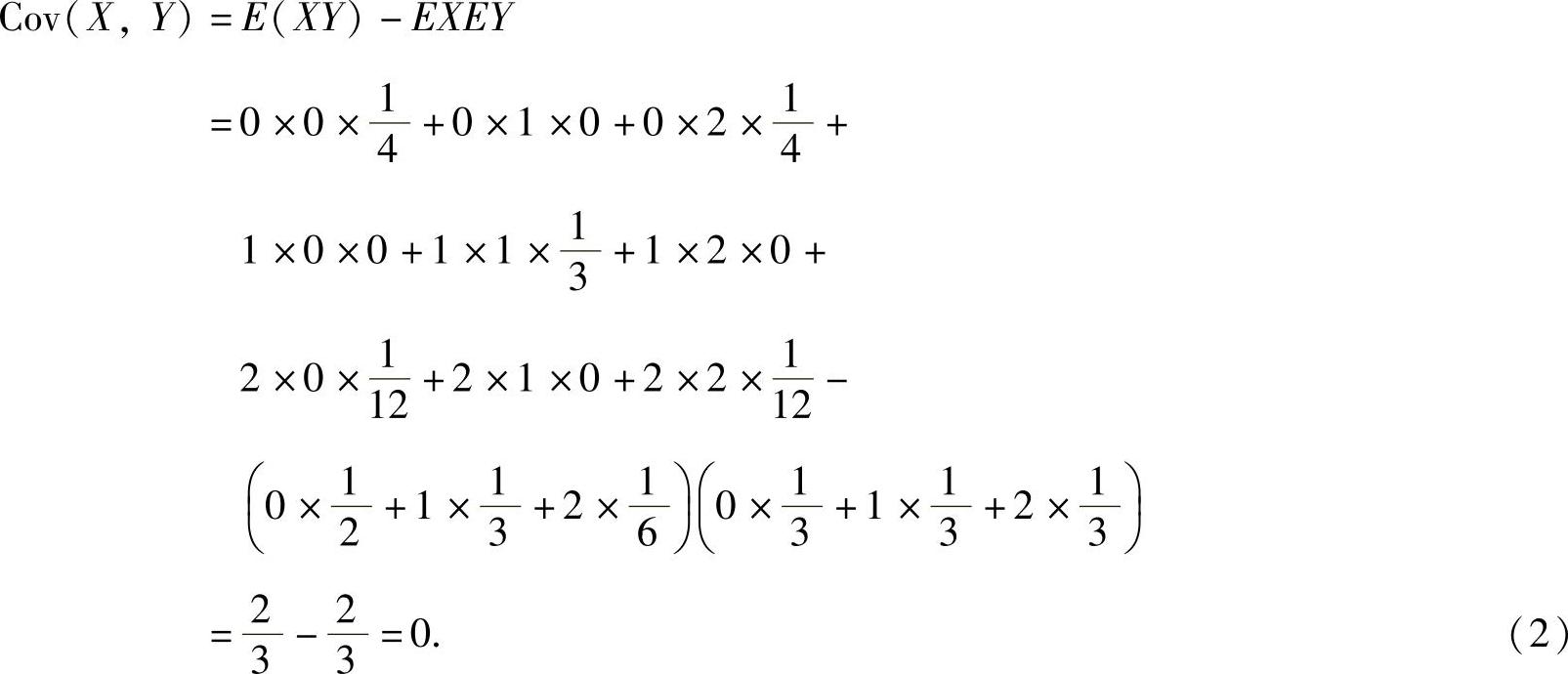
此外,关于Y的边缘概率分布为

所以
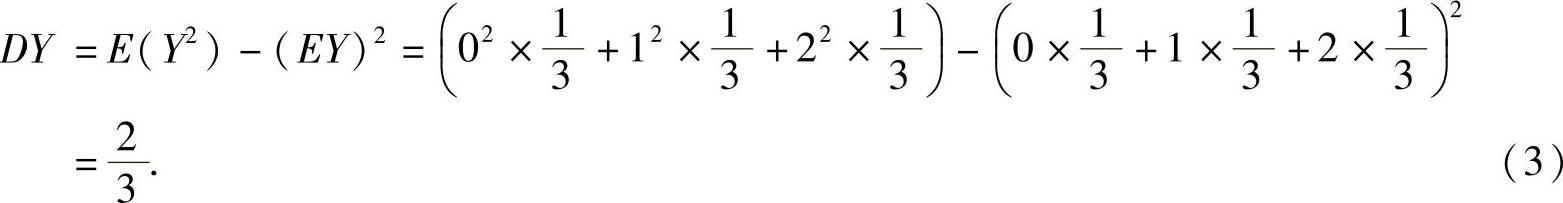
将式(2)、式(3)代入式(1)得
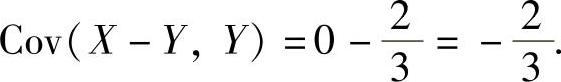
附注 由题解Cov(X-Y,Y)≠0知,X-Y与Y不相互独立的.也可检验如下:
由于
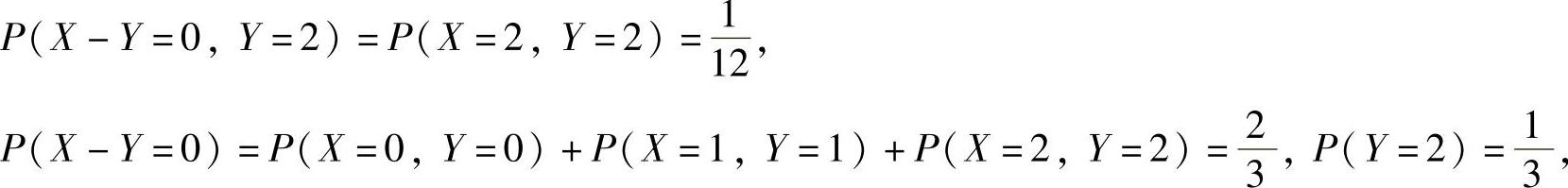
所以
P(X-Y=0,Y=2)≠P(X-Y=0)P(Y=2).
因此X-Y与Y不相互独立.
本题是综合题,其有关内容与计算方法见提高篇21,22,23.
(23)分析 (Ⅰ)先算出V的分布函数FV(v),然后求导得V的概率密度fV(v).
(Ⅱ)利用公式
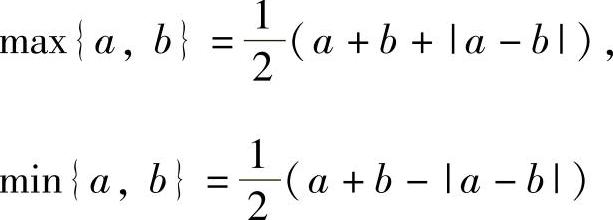
化简U+V,然后计算E(U+V).
精解 (Ⅰ)记V的分布函数为FV(v),则
FV(v)=P(V≤v)=P(min{X,Y}≤v)
=1-P(min{X,Y}>v)=1-P(X>v,Y>v)
=1-P(X>v)P(Y>v) (利用X与Y相互独立)
=1-[1-P(X≤v)][1-P(Y≤v)]
=1-[1-FX(v)][1-FY(v)],
其中FX(v)与FY(v)分别是X与Y的分布函数,且
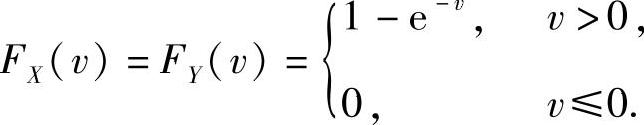
所以
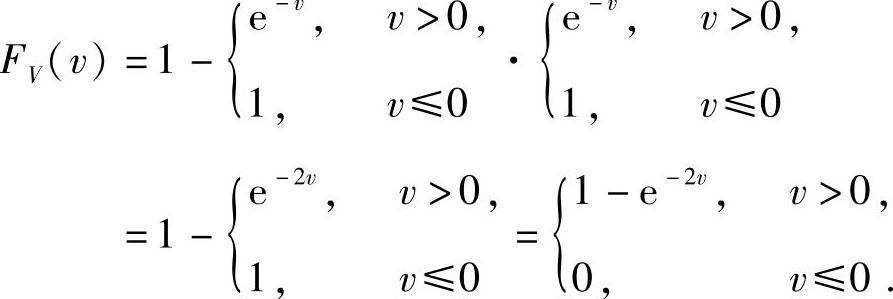
因此V的概率密度
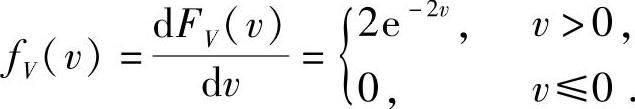
(Ⅱ)利用公式
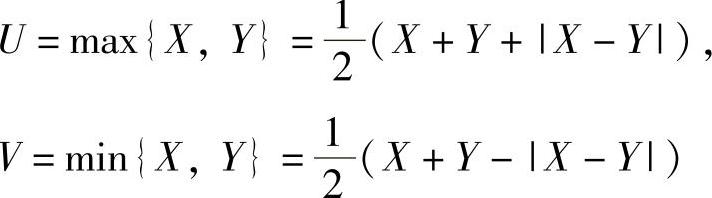
得U+V=X+Y,所以
E(U+V)=E(X+Y)=EX+EY=1+1=2.
附注 应记住以下结论:
设X与Y是相互独立的随机变量,它们的分布函数分别为FX(x)与FY(y),则
(ⅰ)U=max{X,Y}的分布函数为
FU(u)=FX(u)·FY(u),
(ⅱ)V=min{X,Y}的分布函数为
FV(v)=1-[1-FX(v)][1-FY(v)].
本题是综合题,其有关内容及计算方法见提高篇23,24.
