2007年全国硕士研究生入学统一考试试题精解
一、选择题
(1)分析 利用x→0+时的常用等价无穷小寻找与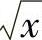 等价的无穷小量.
等价的无穷小量.
精解 由于x→0+时,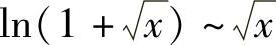 ,所以与
,所以与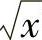 等价的无穷小量是
等价的无穷小量是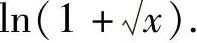
因此本题选(B).
附注 应记住以下的常用等价无穷小:
当x→0时,
sinx~x,tanx~x,arcsinx~x,arctanx~x,
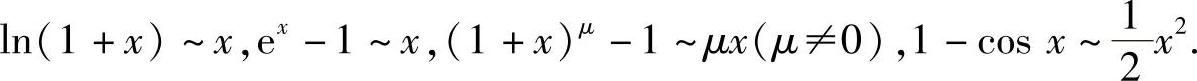
(2)分析 利用函数f(x)在点x=0处连续,排除其中三个正确命题即可.
精解 由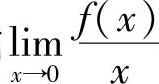 存在知limf(x)=0.于是由f(x)在点x=0处连续得
存在知limf(x)=0.于是由f(x)在点x=0处连续得
x→0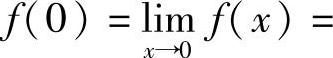
 ,以及
,以及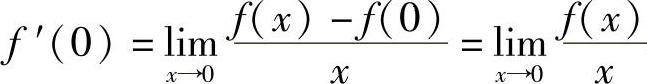 存在.所以选项(A)、(C)都应排除.
存在.所以选项(A)、(C)都应排除.
此外,由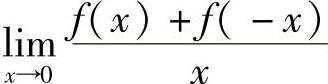 存在知
存在知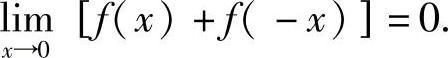 于是由f(x)在点x=0处连续得2f(0)=0,即f(0)=0.所以选项(B)应排除.
于是由f(x)在点x=0处连续得2f(0)=0,即f(0)=0.所以选项(B)应排除.
因此本题选(D).
附注 记住下列结论:
设函数g(x)在点x0处连续,且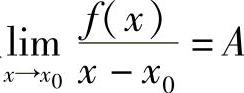 ,则f(x0)=0,f′(x0)=A.
,则f(x0)=0,f′(x0)=A.
(3)分析 由f(x)是奇函数知F(x)是偶函数,所以只要根据定积分的几何意义算出F(2),F(3)即可判定正确选项.
精解 记区间[0,2]、[2,3]上的上、下半圆分别为D1、D2,则

此外,由f(x)是奇函数知F(x)是偶函数,所以
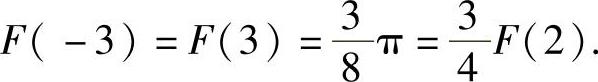
因此本题选(C).
附注 记住以下结论:
设f(x)是连续函数,则当f(x)是奇函数(偶函数)时,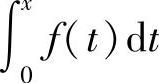 是偶函数(奇函数).
是偶函数(奇函数).
(4)分析 画出所给二次积分对应的二重积分的积分区域D,由此可得先x后y的二次积分.
精解 所给的二次积分对应的二重积分的积分区域为
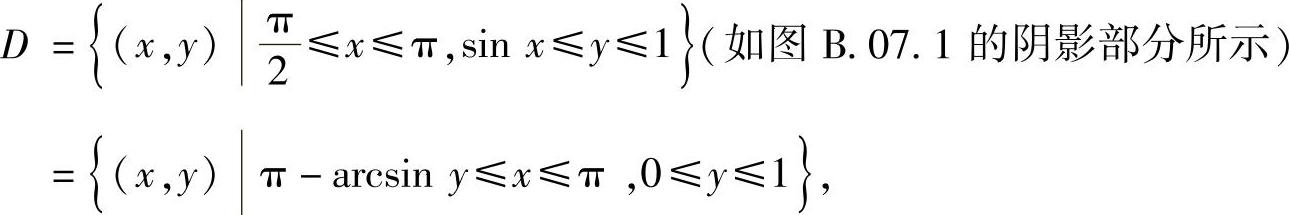
所以,所给的二次积分等于
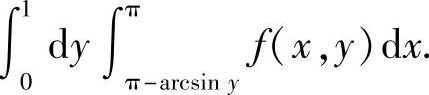
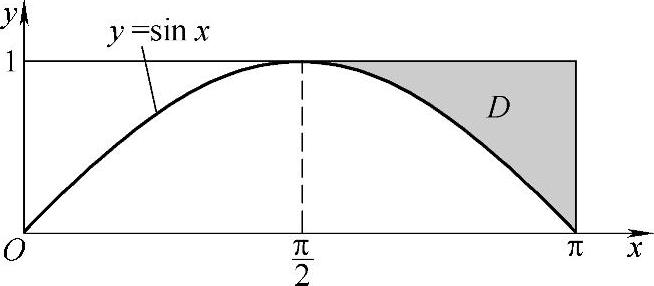
图 B.07.1
因此本题选(B).
附注 变更二次积分的积分次序时,总是先画出所给二次积分对应的二重积分的积分区域.
(5)分析 利用需求弹性的定义计算.
精解 需求弹性εp的绝对值为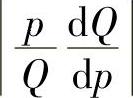 ,于是由题设得
,于是由题设得
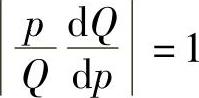 ,即
,即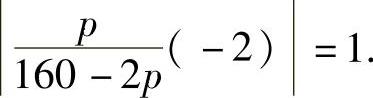
利用p>0,160-2p=Q>0化简上式得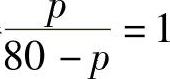 ,所以p=40.
,所以p=40.
因此本题选(D).
附注 由于Q(p)是p的减函数,所以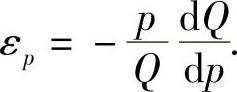
(6)分析 先判断所给曲线有无铅垂渐近线,然后计算非铅垂渐近线,从而得到正确选项.
精解 由于x→0时,y→∞,所以,x=0是曲线的铅垂渐近线.
由于
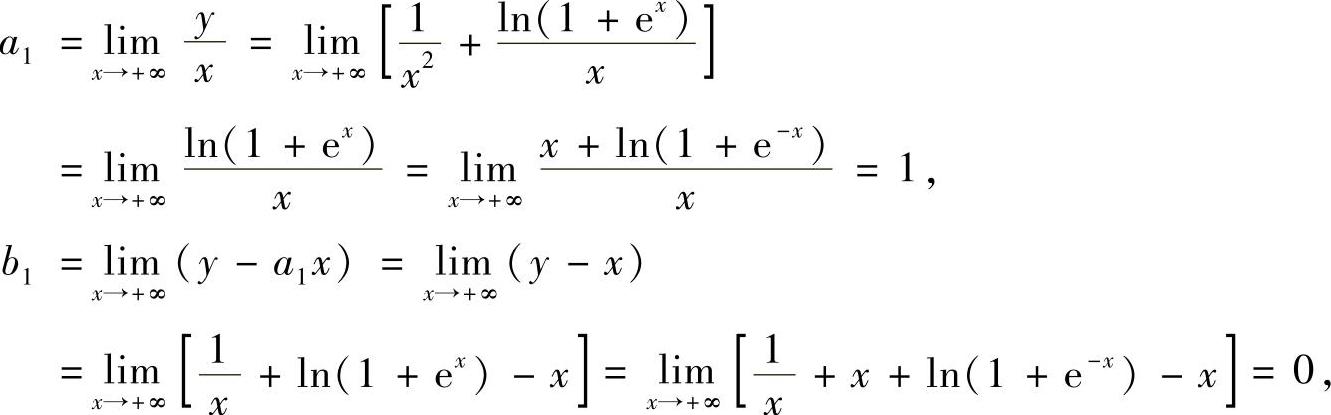
所以曲线有非铅垂渐近线y=x(斜渐近线).
由于
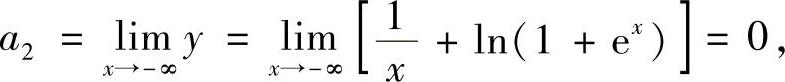
所以曲线有非铅垂渐近线y=0(水平渐近线).
因此本题选(D).
附注 对曲线y=y(x),如果极限
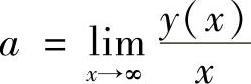 与
与
都存在,则直线y=ax+b是曲线y=y(x)的非铅垂渐近线.如果a或b不存在,则应对式
(1)分别考虑x→+∞和x→-∞的极限.
计算时应注意,如果b=k(常数),则必有非铅垂渐近线y=k(水平渐近线),这是因为此时必有a=0.
(7)分析 按向量组线性相关的定义判断正确选项.
精解 先考虑选项(A).由于
1·(α1-α2)+1·(α2-α3)+1·(α3-α1)=0,所以,向量组α1-α2,α2-α3,α3-α1线性相关.
因此本题选(A).
附注 选项(B)、(C)、(D)的向量组都线性无关,可按以下快捷方法证明:
由于
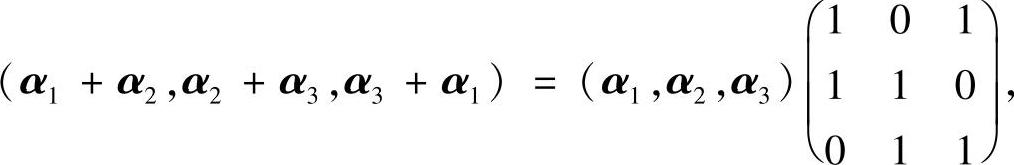
其中向量组α1,α2,α3线性无关,且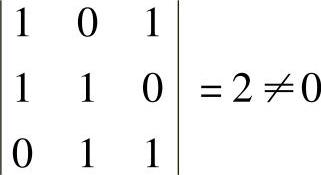 ,所以向量组α1+α2,α2+α3,α3+α1线性无关.同样可证向量组α1-2α2,α2-2α3,α3-2α1线性无关,向量组α1+2α2,α2+2α3,α3+2α1也线性无关.
,所以向量组α1+α2,α2+α3,α3+α1线性无关.同样可证向量组α1-2α2,α2-2α3,α3-2α1线性无关,向量组α1+2α2,α2+2α3,α3+2α1也线性无关.
(8)分析 由于A是实对称矩阵,所以可从计算A的特征值入手.
精解 记E为三阶单位矩阵,则由
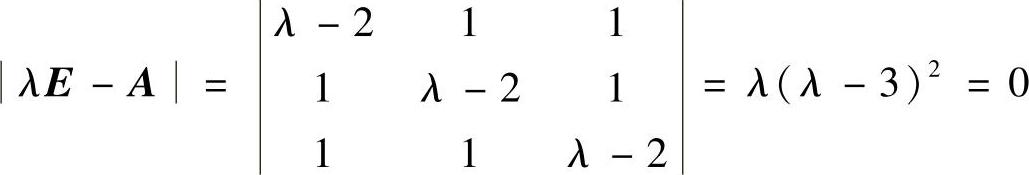
得A的特征值为0,3(二重).
由此可知,两个实对称矩阵A与B的特征值不全相同,所以不相似,但是A与B的正特征值个数、负特征值个数分别相等,所以A与B合同.
因此本题选(B).
附注 (ⅰ)n阶实对称矩阵A与B相似必合同,但合同未必相似.
(ⅱ)n阶实对称矩阵A与B相似的充分必要条件是A与B有相同的特征多项式;合同的充分必要条件是二次型f(x1,x2,…,xn)=xTAx与g(x1,x2,…,xn)=xTBx(其中x=(x1,x2,…,xn)T)有相同的规范形.
(9)分析 随机事件{第4次射击恰好第二次命中目标}是独立随机事件{前3次射击恰好有一次命中目标}与{第4次射击命中目标}之积,由此即可算出要求的概率.
精解 记A={第4次射击恰好第2次命中目标};
B={前3次射击恰好有一次命中目标},
C={第4次射击命中目标},
则
P(A)=P(BC)=P(B)P(C)=C31p(1-p)2·p=3p2(1-p)2.
因此本题选(C).
附注 顺便可以考虑与本题相关的一个问题,即计算此人第4次射击恰好第2次命中目标的条件下第1次命中目标恰好是第3次射击的概率.
记 D={第1次命中目标恰好是第3次射击},则所求的概率为
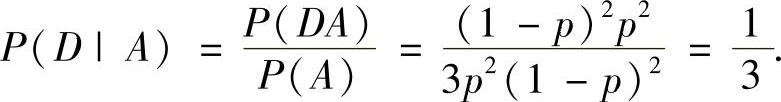
(10)分析 由条件概率密度计算公式即可确定正确的选项.
精解 由于(X,Y)服从二维正态分布,且X与Y互不相关,所以X与Y相互独立.
从而
fX|Y(x|y)=fX(x).
因此本题选(A).
附注 (ⅰ)由于本题的(X,Y)服从二维正态分布,所以对任何y有fY(y)≠0,从而对任何y,fX|Y(x|y)都有意义.
(ⅱ)当随机变量(X,Y)服从二维正态分布时,X与Y相互独立的充分必要条件是X与Y互不相关.
二、填空题
(11)分析 利用“无穷小与有界函数之积为无穷小”的结论计算.
精解 由于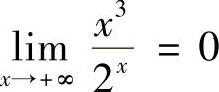 ,所以
,所以
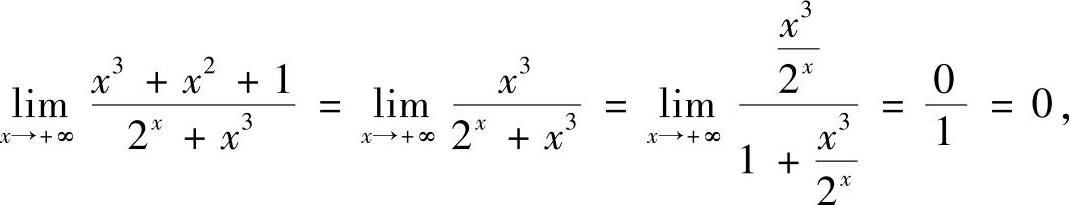
即x→+∞时,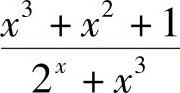 是无穷小,而sinx+cosx≤2,即sinx+cosx是有界函数.因此
是无穷小,而sinx+cosx≤2,即sinx+cosx是有界函数.因此
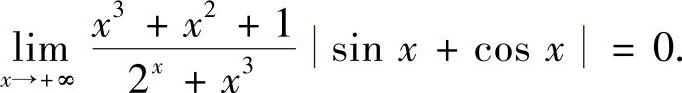
附注 考虑类似的问题:求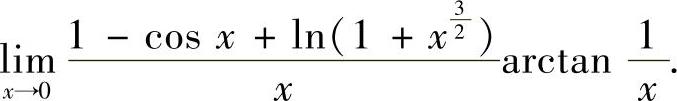
由于
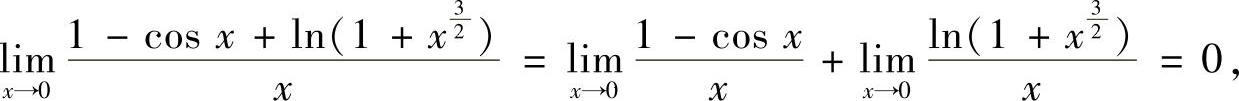
并且在点x=0的去心邻域内 ,所以
,所以
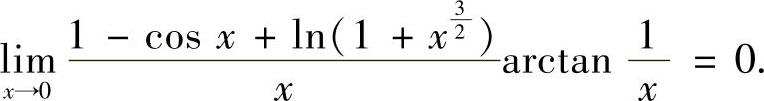
(12)分析 利用y的带佩亚诺型余项的n阶麦克劳林公式计算y(n)(0).
精解 由于
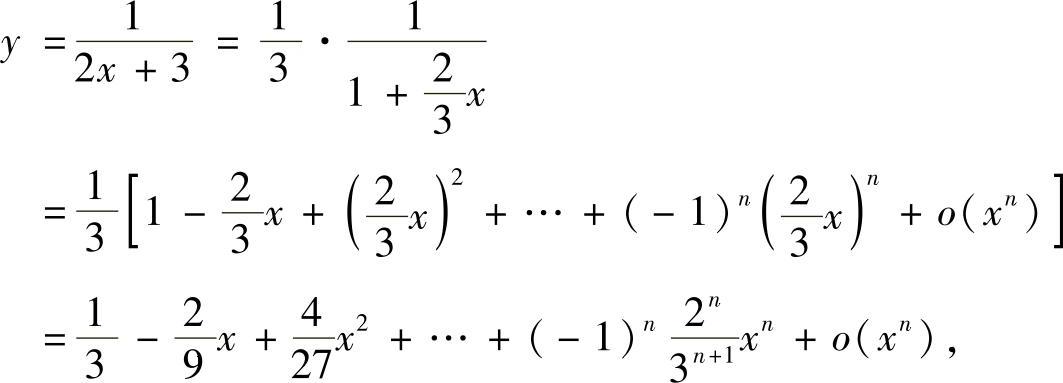
所以
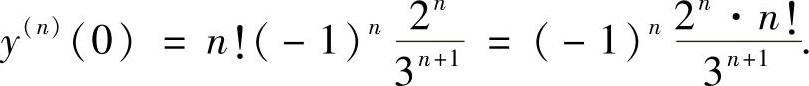
附注 (ⅰ)函数f(x)的带佩亚诺型余项的n阶麦克劳林公式为
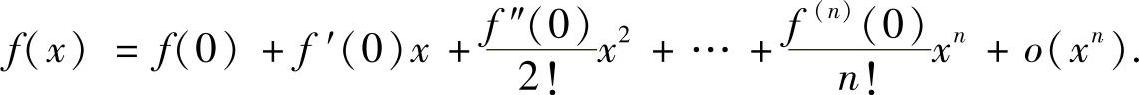
(ⅱ)y(n)(0)也可以按函数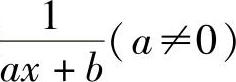 的n阶导数公式
的n阶导数公式
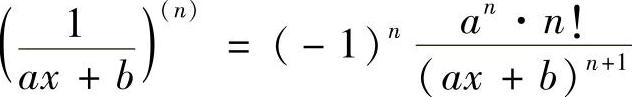
计算得
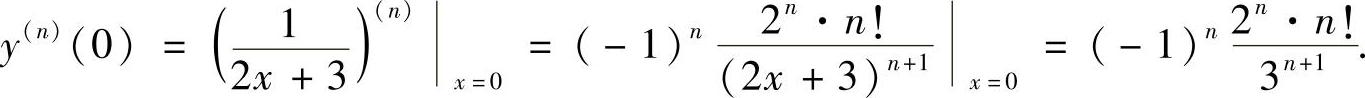
(13)分析 先利用dz算出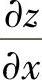 ,
,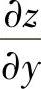 ,然后将它们代入
,然后将它们代入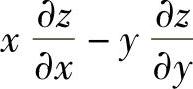 即可.
即可.
精解 由
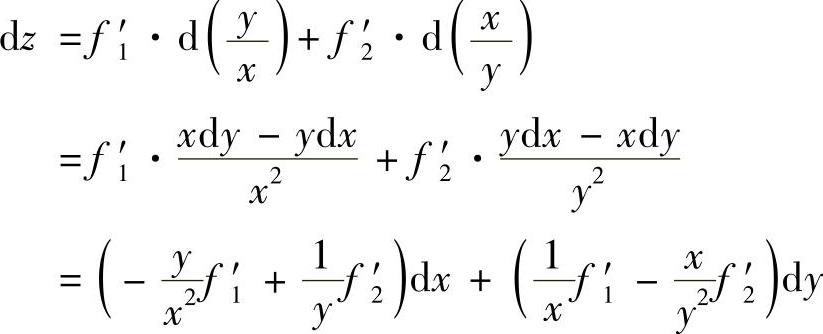
得
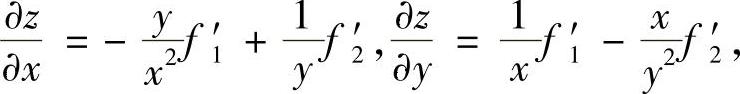
所以
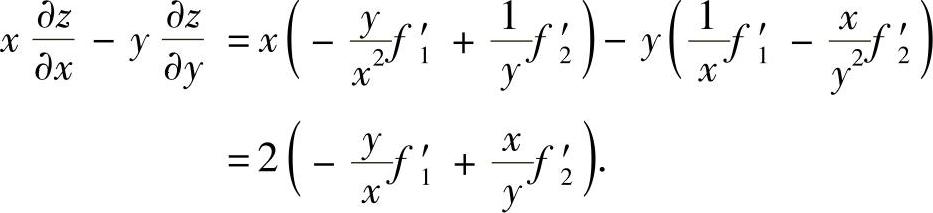
附注 由于要计算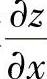 、
、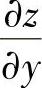 ,所以从计算dz入手,以使计算快捷些.
,所以从计算dz入手,以使计算快捷些.
(14)分析 所给微分方程是一阶齐次微分方程,因此令u=yx进行计算.
精解 令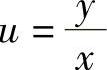 ,则所给微分方程成为
,则所给微分方程成为
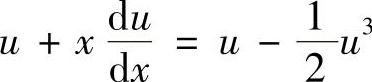 ,即
,即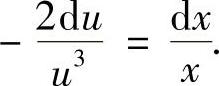
两边积分得

将y(1)=1,即u(1)=1代入式(1)得
1=0+C,即C=1.
将它代入式(1)得
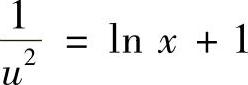 ,即
,即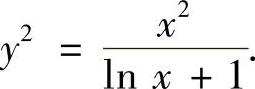
解出y得
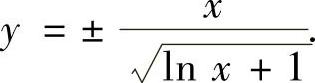
由于y(1)=1,所以上式右边只能取正号,因此所求的特解为
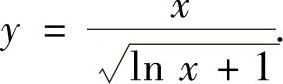
附注 所给微分方程的通解也可以按以下方法计算:
将所给微分方程改写为
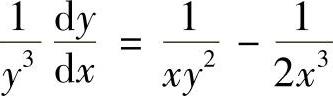 ,即
,即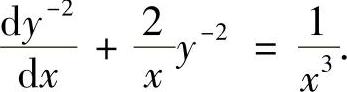
令v=y-2得
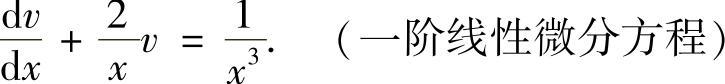 (https://www.daowen.com)
(https://www.daowen.com)
它的通解为
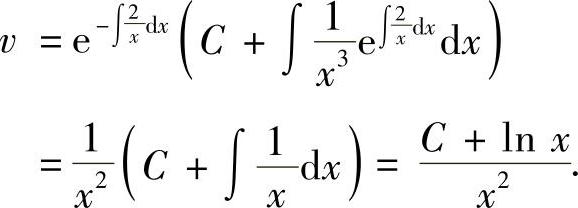
因此所给微分方程的通解为
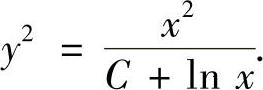
(15)分析 只要算出A3,即可得到A3的秩.
精解 由于

所以A3的秩为1.
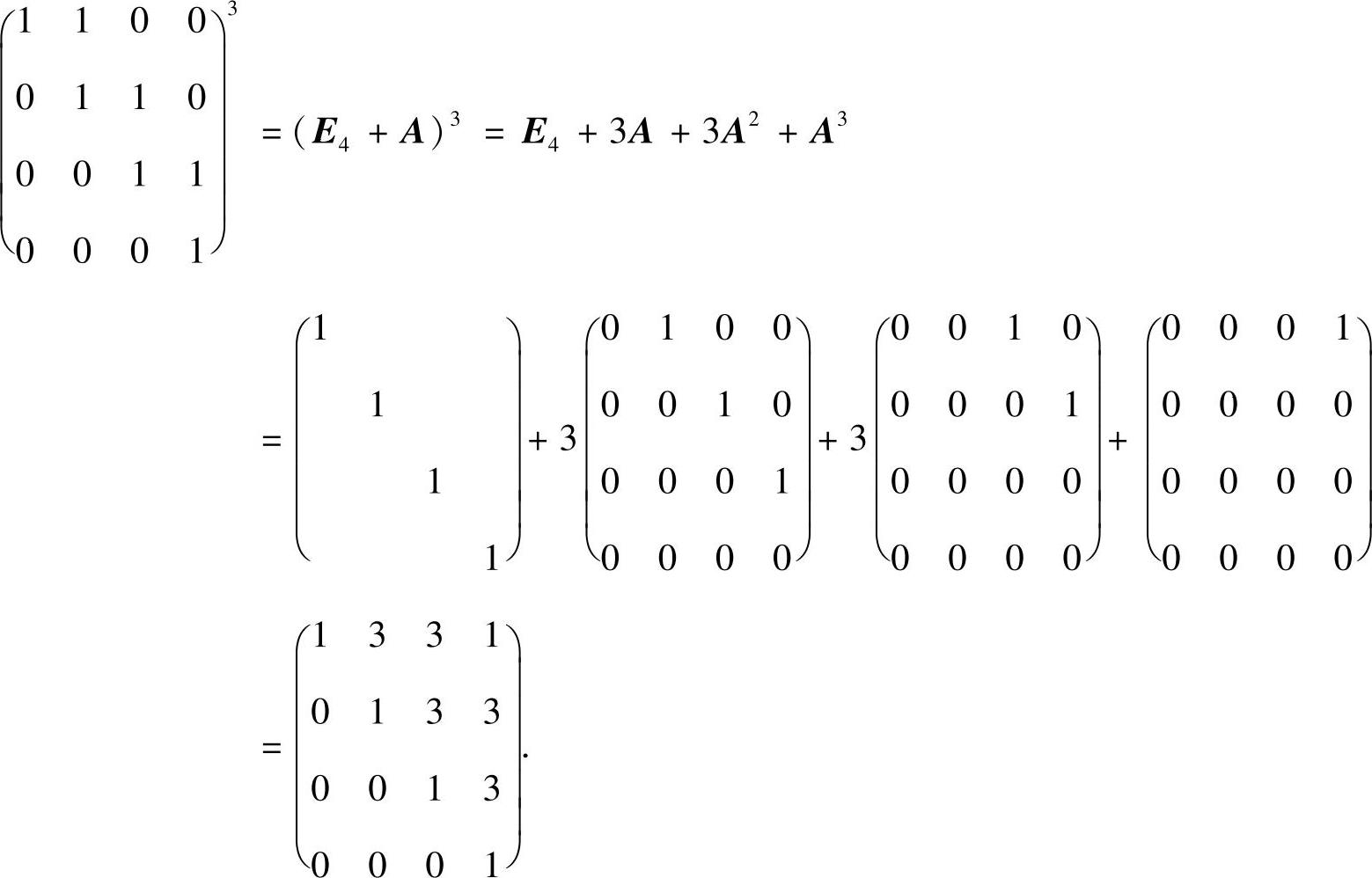
附注 顺便考虑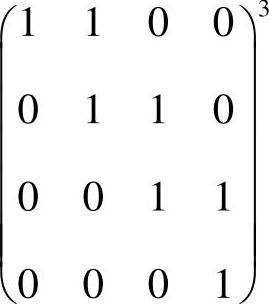 ,它可快捷计算如下:
,它可快捷计算如下:
由于

所以
(16)分析 设两个数为X,Y,则它们是相互独立的随机变量,且都服从(0,1)内的均匀分布.
精解 (X,Y)的概率密度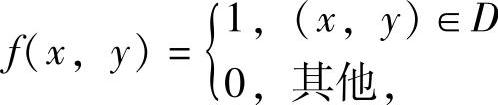 ,其中D={(x,y)0≤x≤1,0≤y≤1},所以所求的概率为
,其中D={(x,y)0≤x≤1,0≤y≤1},所以所求的概率为

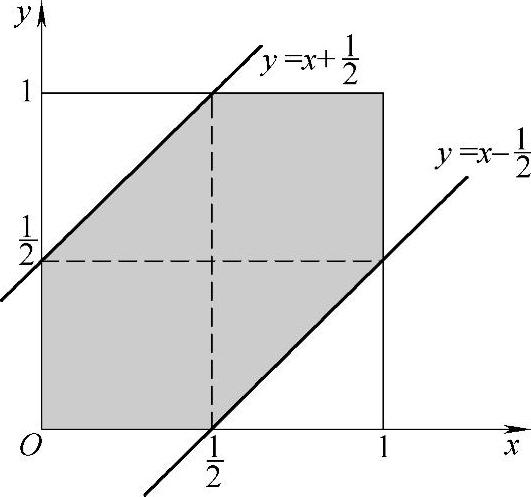
图 B.07.2
附注 “在区间(0,1)内随机地取两个数”,表明这两个数X,Y相互独立,且都在(0,1)内服从均匀分布.
三、解答题
(17)分析 求出函数y=y(x)在点x=1附近的二阶导数,并判定它的正负性.
精解 所给方程两边对x求导得
y′lny+y′-1+y′=0,
即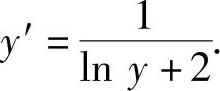 于是
于是
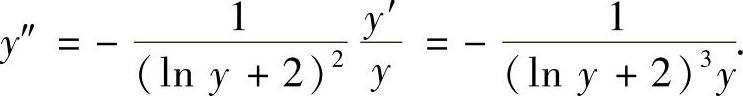
显然在点(1,1)附近y″<0.因此在点(1,1)附近曲线y=y(x)是凸的.
附注 由题解中计算可知,曲线y=y(x)在点(1,1)附近是单调上升且是凸的.此外曲线y=y(x)有拐点(-e-2,e-2).
(18)分析 利用D的对称性把所给二重积分化简为4∬D1f(x,y)dσ,其中D1是D的第一象限部分.然后用直线x+y=1将D1分成D2、D3两部分(如图B.07.3所示),且分别计算f(x,y)在D2和D3上的二重积分.
精解 由于D关于x轴和y轴都对称,且在对称点处f(x,y)的值彼此相等,所以
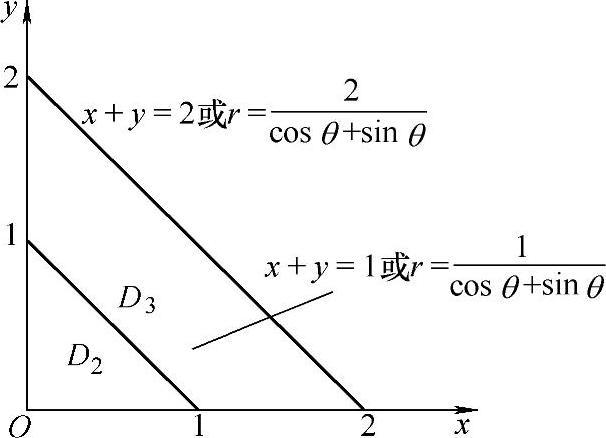
图 B.07.3
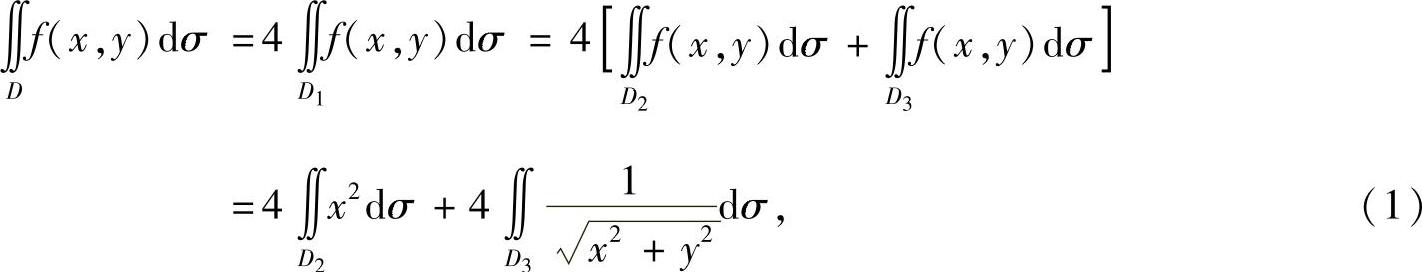
其中 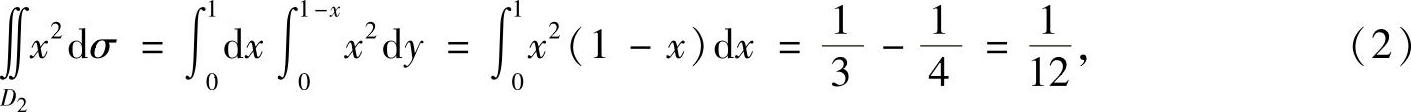


将式(2)、式(3)代入式(1)得
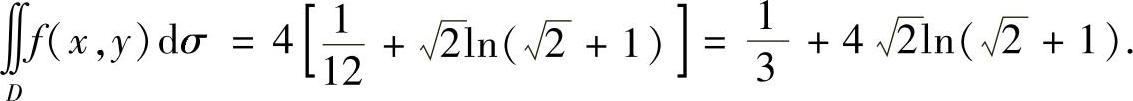
附注 由于D2是角域的一部分,所以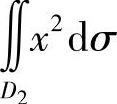 也可以用极坐标计算,具体如下:
也可以用极坐标计算,具体如下:
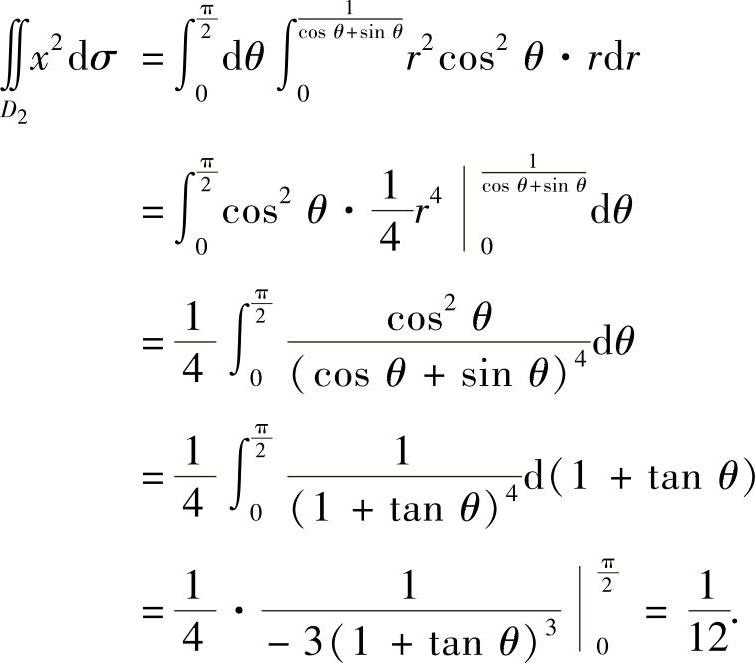
本题的计算方法见提高篇12.
(19)分析 作辅助函数F(x)=f(x)-g(x),则欲证的问题成为:(Ⅰ)存在η∈(a,b),使得F(η)=0;(Ⅱ)存在ξ∈(a,b),使得F″(ξ)=0.显然需两次应用罗尔定理.
精解 (Ⅰ)作辅助函数F(x)=f(x)-g(x),显然F(a)=F(b)=0.此外存在c,d∈(a,b),使得f(c)=f(d)=M(f(x)与g(x)在[a,b]上的最大值).如果c≠d,则F(c)=f(c)-g(c)≥0,F(d)=f(d)-g(d)≤0.于是由零点定理(推广形式)知,存在η∈[c,d]或[d,c],使得F(η)=0.如果c=d,则可取η=c.从而有f(η)=g(η)(η∈(a,b)).
(Ⅱ)由(Ⅰ)可知,在[a,b]上有不同三点a,η,b,使得F(a)=F(η)=F(b),并且F(x)在[a,b]上连续,在(a,b)内可导,所以对F(x)在[a,η]和[η,b]上分别应用罗尔定理知,存在ξ1∈(a,η)和ξ2∈(η,b),使得F′(ξ1)=F′(ξ2)=0.此外,F′(x)在[ξ1,ξ2]上可导,所以再由罗尔定理知,存在ξ∈(ξ1,ξ2)⊂(a,b),使得F″(ξ)=0,即f″(ξ)=g″(ξ).
附注 (ⅰ)零点定理有各种推广形式,例如:
设函数f(x)在[a,b]上连续,f(a)f(b)≤0,则存在ξ∈[a,b],使得f(ξ)=0.
设函数f(x)在[a,+∞)上连续,f(a)·
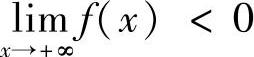 ,则存在ξ∈(a,+∞),使得f(ξ)=0.
,则存在ξ∈(a,+∞),使得f(ξ)=0.
(ⅱ)罗尔定理也有各种推广形式,例如:
设函数f(x)在[a,b]上连续,在(a,b)内二阶可导,且f(x1)=f(x2)=f(x3)(其中a≤x1<x2<x3≤b),则存在ξ∈(a,b),使得f″(ξ)=0.
设函数f(x)在[a,b]上连续可导,在(a,b)内二阶可导,且f′(ξ1)=f′(ξ2)(其中a≤ξ1<ξ2≤b),则存在ξ∈(a,b),使得f″(ξ)=0.
本题的有关内容与证明方法见提高篇04.
(20)分析 令t=x-1,将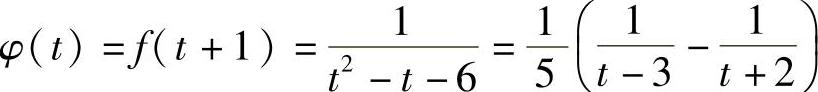 展开成t的幂级数即可.
展开成t的幂级数即可.
精解 由于
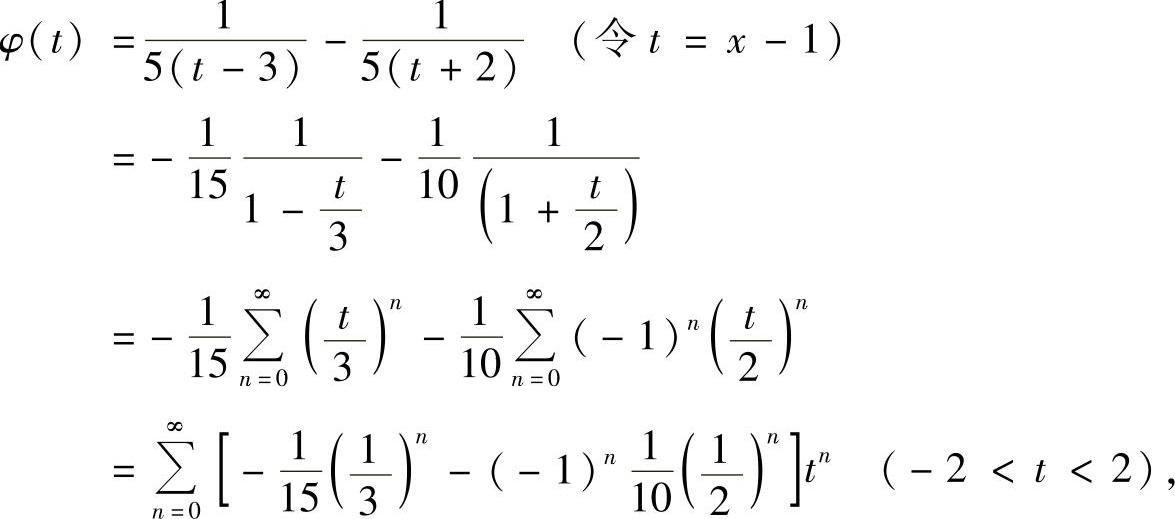
所以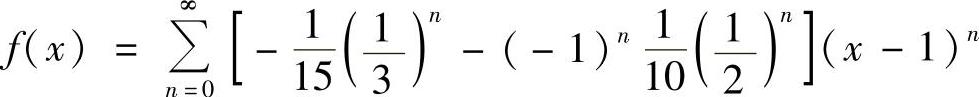 (-2<x-1<2,即-1<x<3).
(-2<x-1<2,即-1<x<3).
附注 将函数f(x)展开成x-x0的幂级数的步骤如下:
(ⅰ)令t=x-x0,记φ(t)=f(t+x0).
(ⅱ)将φ(t)表示成常用函数的线性组合,或常用函数的积分上限函数,或常用函数的导数,这里线性组合的系数可以为常数或t的正整数幂,而常用函数是指eax,sin ax,cos ax,ln(1+ax),(1+ax)μ(其中a是常数).
(ⅲ)将φ(t)中的各个常用函数用对应的麦克劳林级数代入,通过幂级数的代数运算或分析运算,算出φ(t)的关于t的幂级数展开式,其成立范围为代入到φ(t)的各个麦克劳林级数的收敛域的公共部分,记为-R<t<R.
(ⅳ)将t=x-x0代入φ(t)的幂级数展开式,就将f(x)展开成x-x0的幂级数,其成立范围为-R<x-x0<R,即x0-R<x<x0+R.
本题的有关内容及计算方法见提高篇14.
(21)分析 将所给线性方程组与方程联立构成新的线性方程组,由此,问题变成新的线性方程组有解时,计算a的值及所有解.
精解 由所给线性方程组及方程构造线性方程组
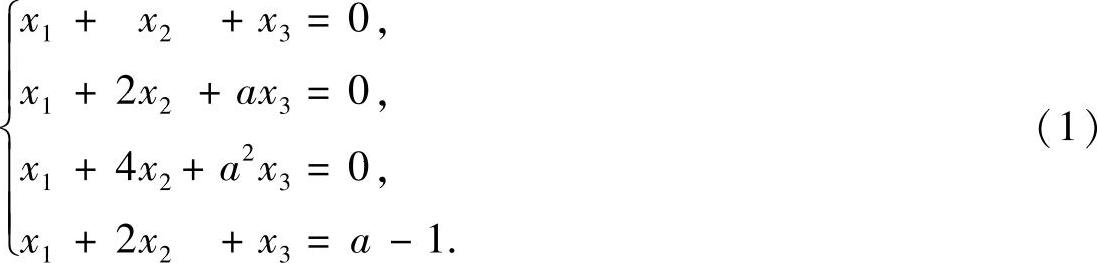
对它的增广矩阵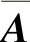 施行初等行变换:
施行初等行变换:
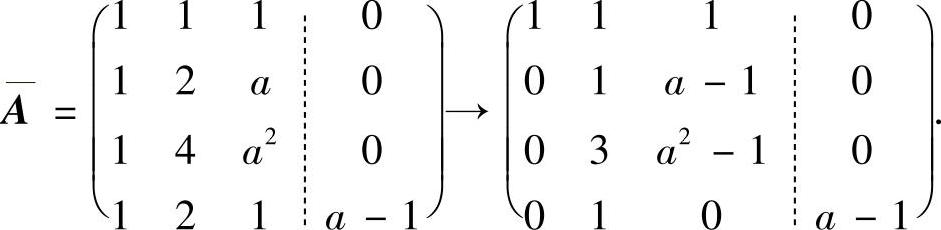
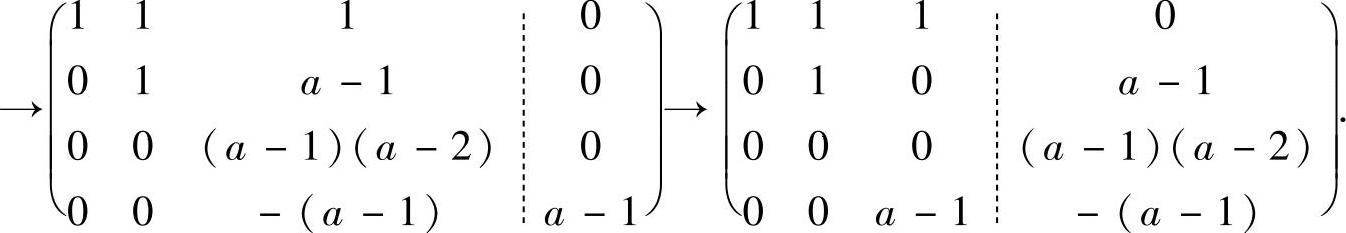
由于式(1)有解(即所给线性方程组与方程有公共解),所以r(A)=r(A)(A是式(1)的系数矩阵).由此得到(a-1)(a-2)=0,即a=1,2.
当a=1时,式(1)与方程组
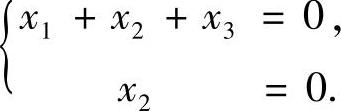
同解,所以式(1)的解,即所求的公共解为
(x1,x2,x3)T=C(-1,0,1)T (C是任意常数).
当a=2时,式(1)与方程组
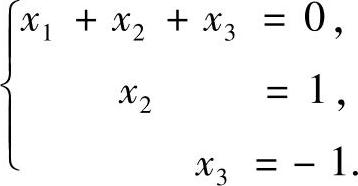
同解,所以式(1)的解,即所求的公共解为
(x1,x2,x3)T=(0,1,-1)T.
附注 线性方程组
A1x=b1与A2x=b2
(其中A1,A2分别是m1×n与m2×n矩阵)有公共解的充分必要条件是方程组
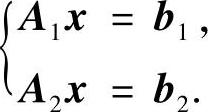
有解.
本题的有关内容与计算方法见提高篇18.
(22)分析 (Ⅰ)记f(λ)=λ5-4λ3+1,则B的所有特征值为μ1=f(λ1),μ2=f(λ2),μ3=f(λ3).于是只要算出A的特征向量,即能得到B的所有特征向量.
(Ⅱ)利用B与对角矩阵正交相似算出B.
精解 (Ⅰ)由于Bα1=A5α1-4A3α1+α1=15·α1-4·13·α1+α1=-2α1,且α1≠0,所以α1是B的对应特征值-2的一个特征向量.
由B=A5-4A3+E,记f(λ)=λ5-4λ3+1,所以由A的特征值为1,2,-2得B的特征值为μ=f(1)=-2,f(2)=1,f(-2)=1.
B的对应μ=-2的全部特征向量为Cα1=C(1,-1,1)T(其中C是任意非零常数).
设B的对应μ=1的特征向量为x=(x1,x2,x3)T,则由A是实对称矩阵知B是实对称矩阵,所以有
α1·x=0,即x1-x2+x3=0.
它的基础解系为α2=(1,1,0)T,α3=(-1,0,1)T,所以B的对应μ=1的全部特征向量为
C1(1,1,0)T+C2(-1,0,1)T=(C1-C2,C1,C2)T,
其中C1,C2是任意不全为零的常数.
(Ⅱ)为了构造正交矩阵Q,将α1,α2,α3正交单位化.显然只要将α2,α3正交化即可.
η2=α2=(1,1,0)T,
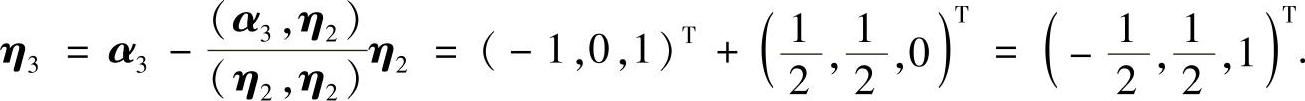
然后单位化:
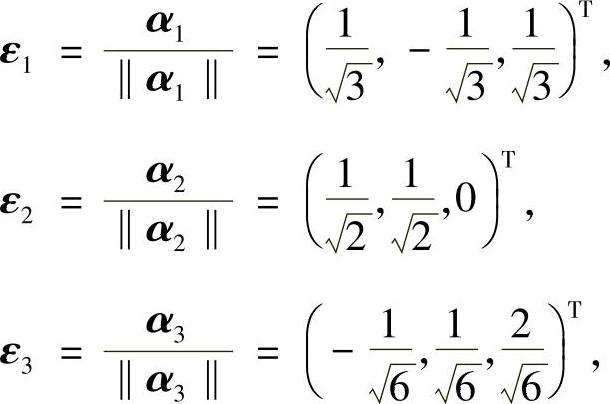
记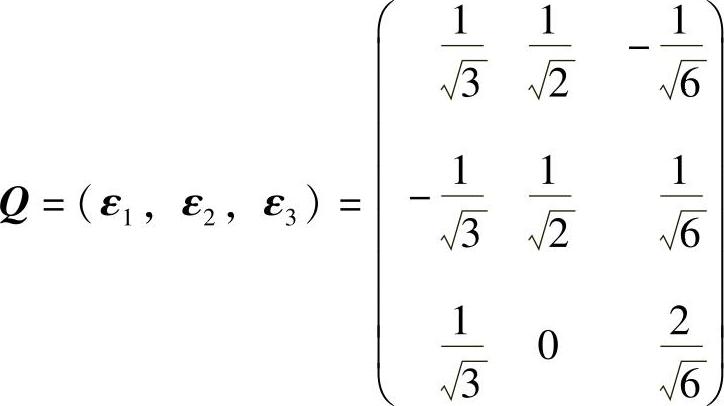 (正交矩阵),则
(正交矩阵),则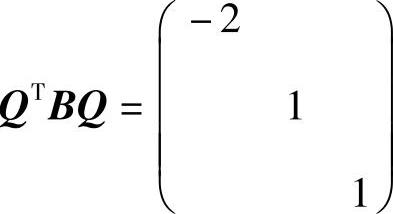 ,所以
,所以

附注 B也可以按与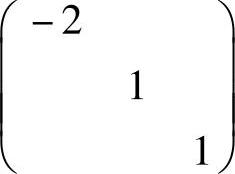 相似的方法计算,具体如下:
相似的方法计算,具体如下:
记P=(α1,α2,α3),则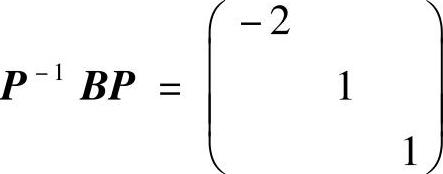 ,所以只要算P-1即可得
,所以只要算P-1即可得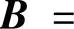
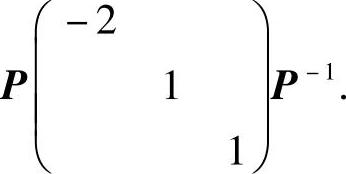
但是,在计算实对称矩阵B时,以构造正交矩阵Q,并且按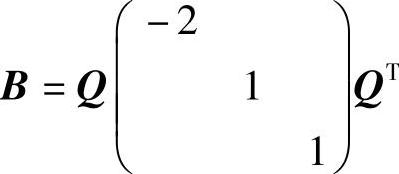 计算为宜.
计算为宜.
(23)分析 (Ⅰ)对f(x,y)在D1={(x,y)|x>2y}上积分即可得到P(X>2Y).
(Ⅱ)利用公式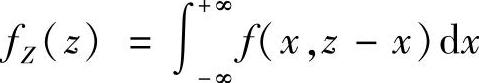 计算fZ(z).
计算fZ(z).
精解 (Ⅰ)记D={(x,y)|0<x<1,0<y<1},D1={(x,y)|x>2y},则D∩D1如图B.07.4a阴影部分所示.于是
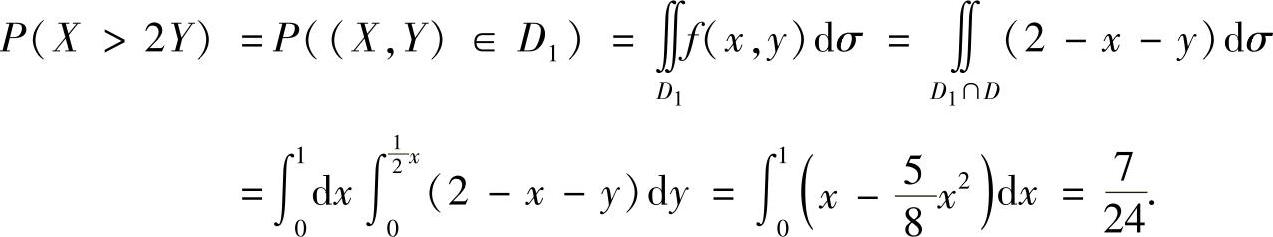
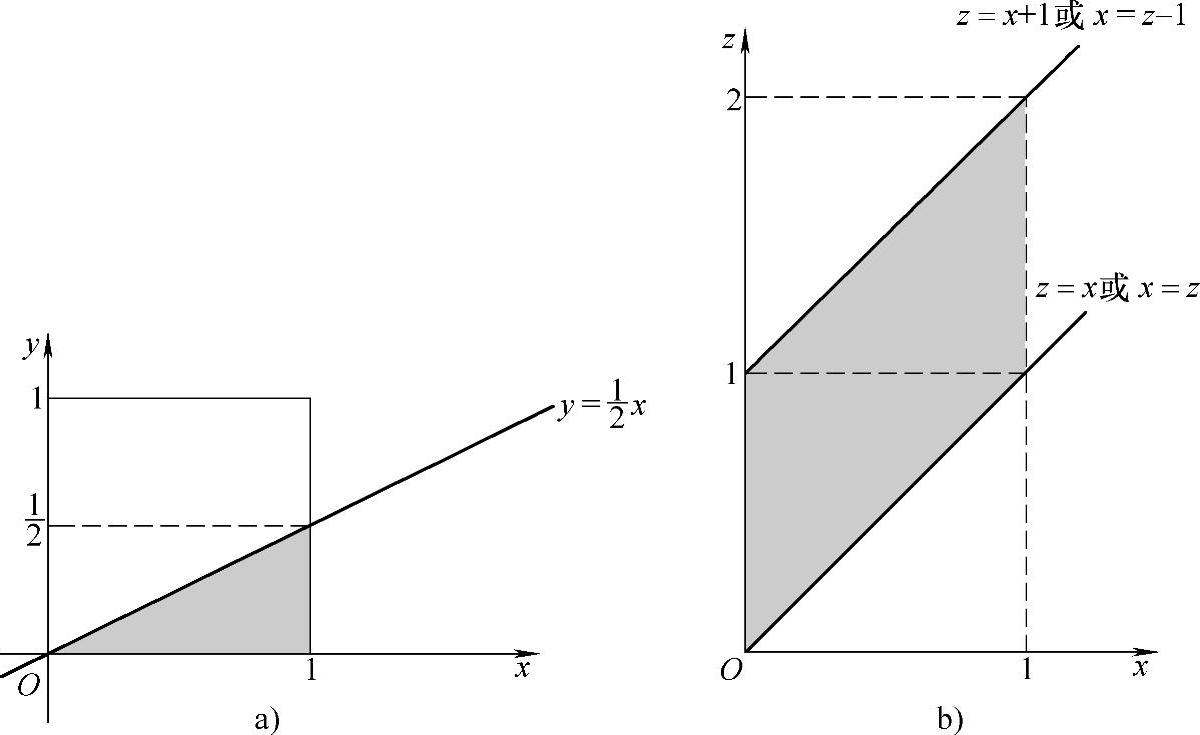
图 B.07.4
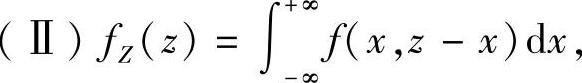
其中 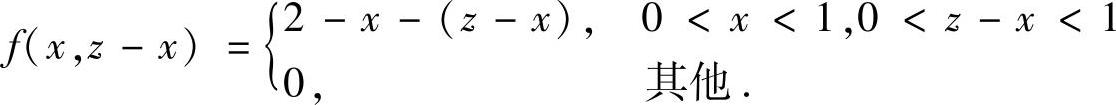
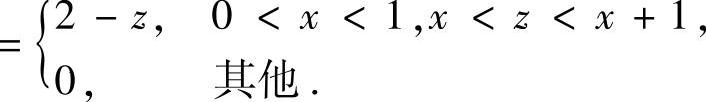
即f(x,z-x)仅在图B.07.4b阴影部分取值为2-z,在xOz平面的其他部分都取值为零.所以由图可知

附注 应记住以下结论:
设二维随机变量(X,Y)的概率密度为f(x,y)(-∞<x<+∞,-∞<y<+∞),则随机变量Z=aX+bY+c的概率密度为
当b≠0时,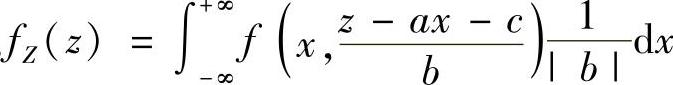 ,
,
当a≠0时,f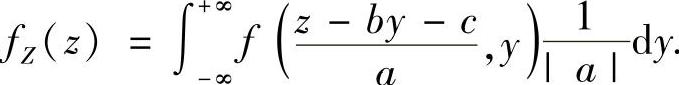 特别地,有
特别地,有
随机变量Z1=X+Y的概率密度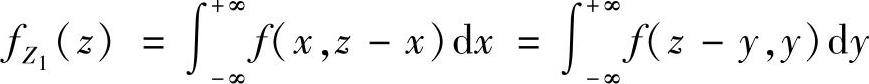 ,随机变量Z2=X-Y的概率密度
,随机变量Z2=X-Y的概率密度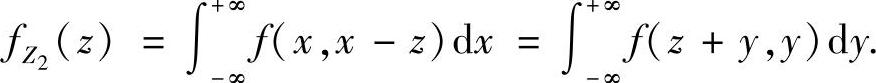
本题是综合题,其有关内容及计算方法见提高篇21,23.
(24)分析
(Ⅰ)计算EX,令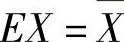 算出θ的矩估计量.
算出θ的矩估计量.
(Ⅱ)计算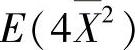 即可得知
即可得知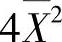 是否为θ2的无偏估计量.
是否为θ2的无偏估计量.
精解 (Ⅰ)因为
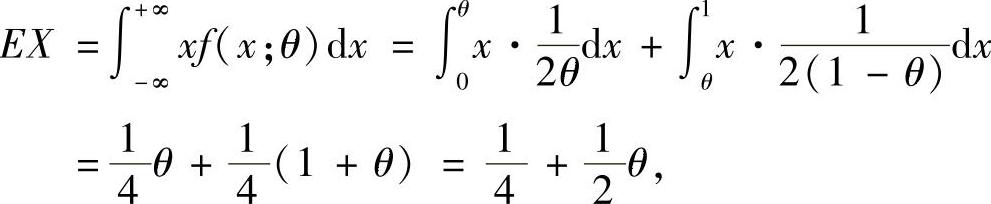
所以,由矩估计法,令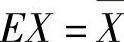 ,即
,即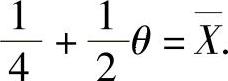 解出θ,即得θ的矩估计量为
解出θ,即得θ的矩估计量为
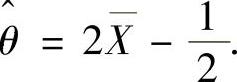
(Ⅱ)由 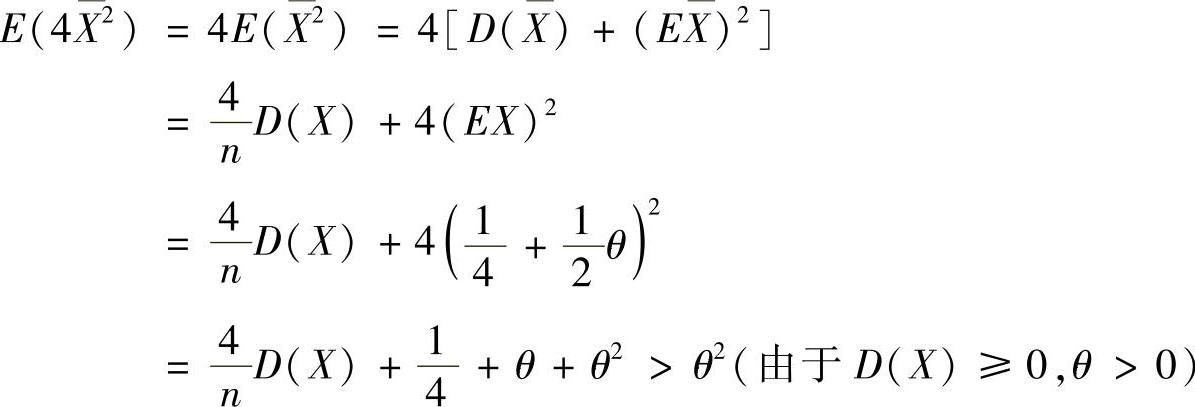
知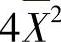 不是θ2的无偏估计量.
不是θ2的无偏估计量.
附注 题解中不必算出DX的值,现在作为练习具体计算如下:
DX=E(X2)-(EX)2,(1)
其中 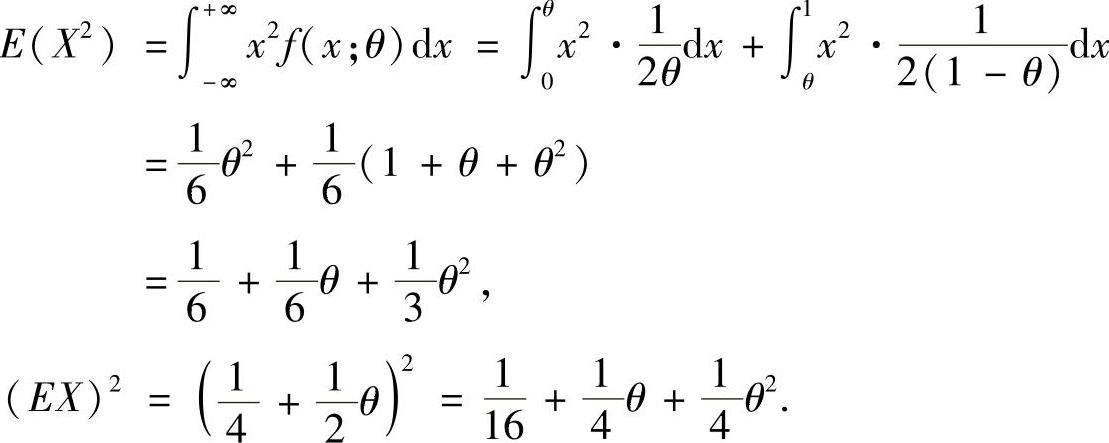
将它们代入式(1)得
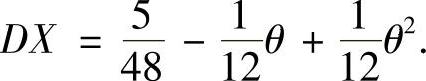
本题的有关内容与计算方法见提高篇26.
