2009年全国硕士研究生入学统一考试试题精解
一、选择题
(1)分析 先确定函数f(x)的间断点,然后从中选出可去间断点.
精解 函数f(x)的间断点即为sinπx的零点,所以有x=0,±1,±2,…,其中

此外,对n=2,3,…,由
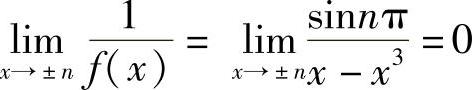
知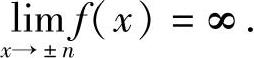
所以f(x)的可去间断点有3个,即x=0,-1,1.
因此本题选(C).
附注 初等函数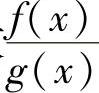 的间断点都来自g(x)的零点.
的间断点都来自g(x)的零点.
(2)分析 由所给的四个选项可知,本题可在a、b都不为零的情形下考虑.
精解 由于
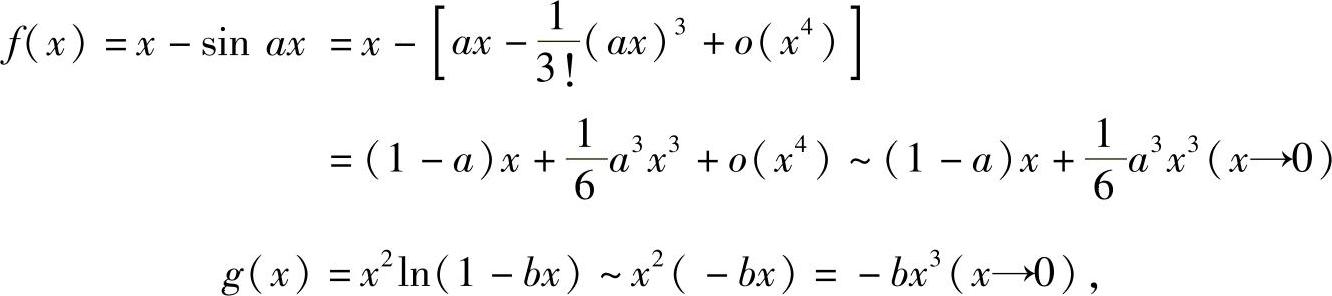
所以当f(x)~g(x)(x→0)时,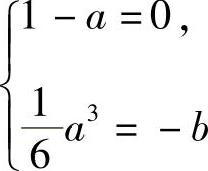 即a=1,,
即a=1,,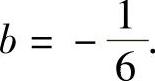
因此本题选(A).
附注 寻找x→x0时函数h(x)的等价无穷小的步骤如下:
(ⅰ)作变量代换t=x-x0,按以下方法寻找φ(t)=h(t+x0)在t→0时的等价无穷小.
(a)利用常用函数在t→0时的等价无穷小.
sint~t,arcsint~t,tant~t,arctant~t,
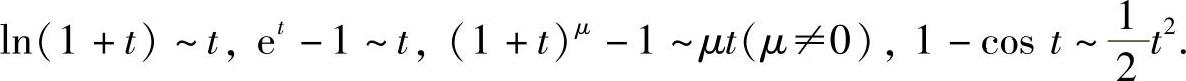
(b)利用常用函数的带佩亚诺型余项的麦克劳林公式:t→0时,
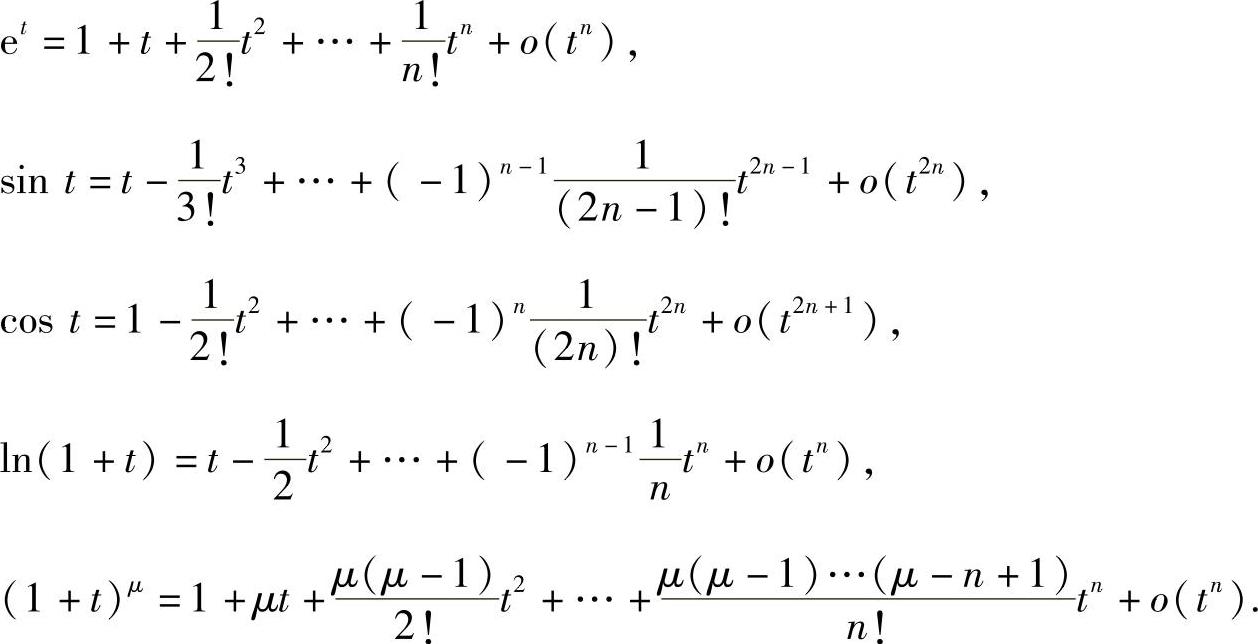
(ⅱ)在(ⅰ)中算得的等价无穷小中令t=x-x0,即得x→x0时h(x)的等价无穷小.
(3)分析 记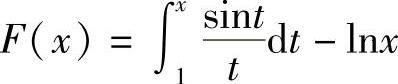 ,然后用导数方法确定使F(x)单调的选项即可.
,然后用导数方法确定使F(x)单调的选项即可.
精解 先考虑选项(A).
由于函数F(x)在(0,1)上可导且
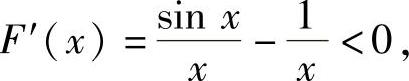
所以F(x)在(0,1)内单调减少,从而有F(x)>F(1)=0,即
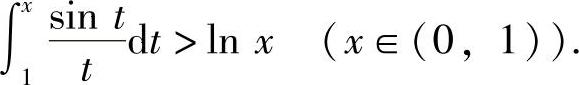
因此本题选(A).
附注 可导函数f(x)的单调性总是用导数方法来确定.
(4)分析 按积分上限函数的性质,排除其中三个不正确的选项即可.
精解 当-1≤x<0时,函数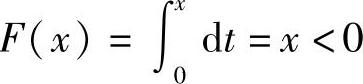 ,所以选项(A)、(C)应排除.
,所以选项(A)、(C)应排除.
函数f(x)在[0,3]上除点x=2是第一类间断点外,处处连续,即f(x)在[0,3]上可积,从而函数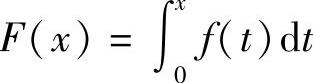 在[0,3]上连续,所以选项(B)也应排除.
在[0,3]上连续,所以选项(B)也应排除.
因此本题选(D).
附注 积分上限函数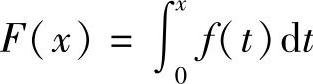 有以下性质:
有以下性质:
(ⅰ)设f(x)在[a,b]上可积,则F(x)在[a,b]上连续;
(ⅱ)设f(x)在[a,b]上连续,则F(x)在[a,b]上可导,且F′(x)=f(x).
(5)分析 通过矩阵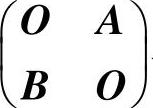 与选项中的矩阵相乘,判定正确选项.
与选项中的矩阵相乘,判定正确选项.
精解 记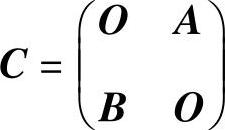 ,则|C|=|A||B|=6.先考虑选项(A).
,则|C|=|A||B|=6.先考虑选项(A).
由于
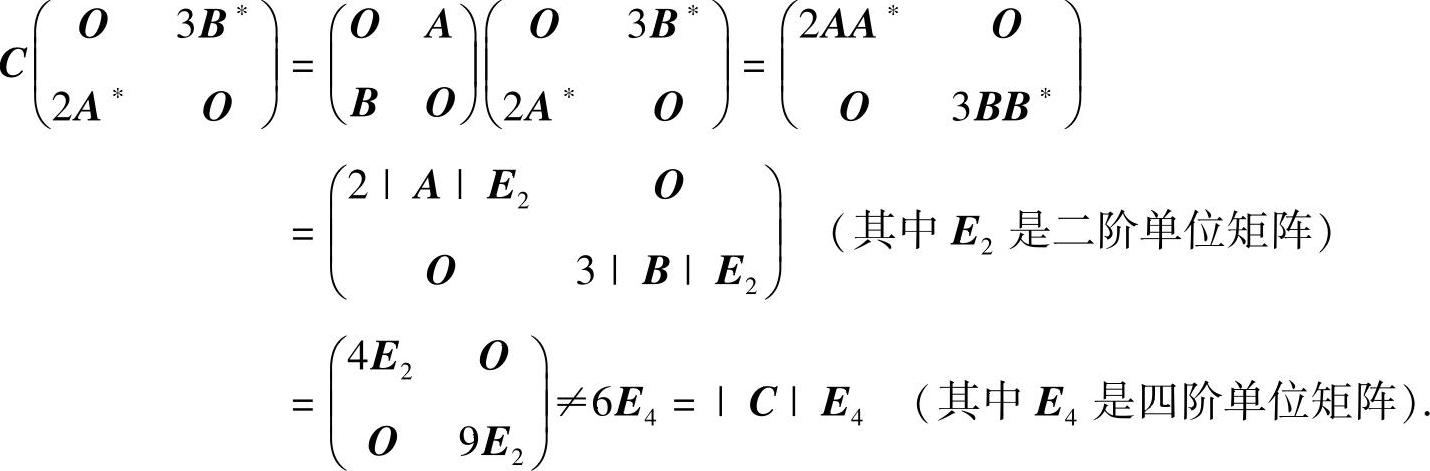
所以排除选项(A),再考虑选项(B).
由于
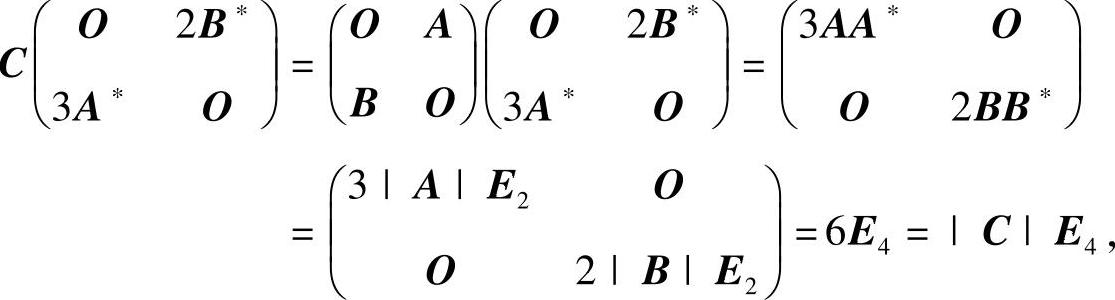
所以 的伴随矩阵是
的伴随矩阵是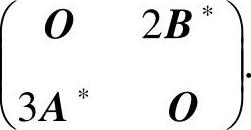
因此本题选(B).
附注 记住以下公式是有用的:
设M1,M2都是方阵,则
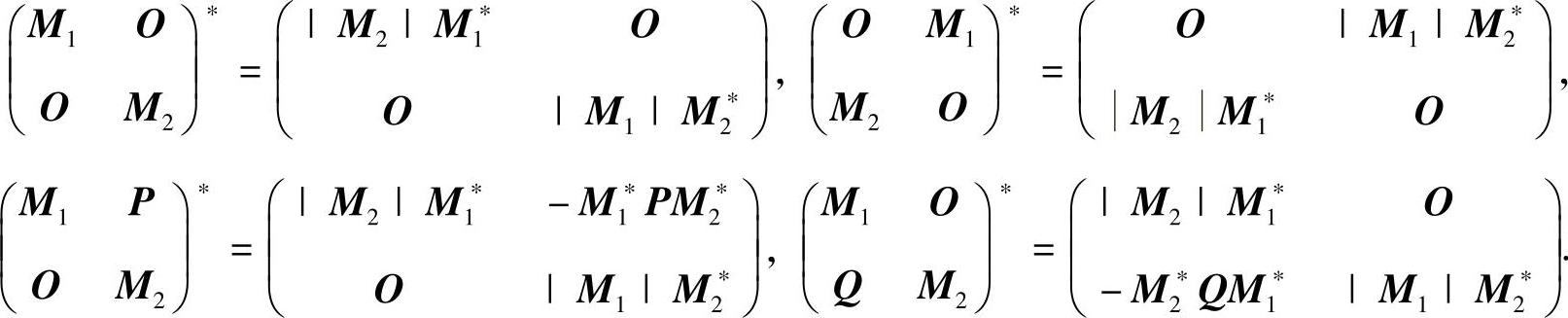
(6)分析 将Q用P表示后,代入QTAQ进行运算即可.
精解 由于
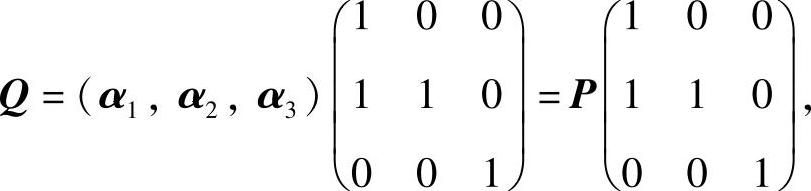
所以
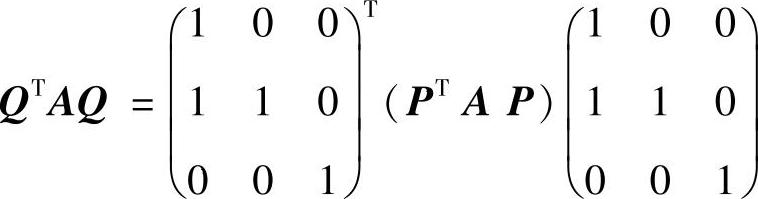
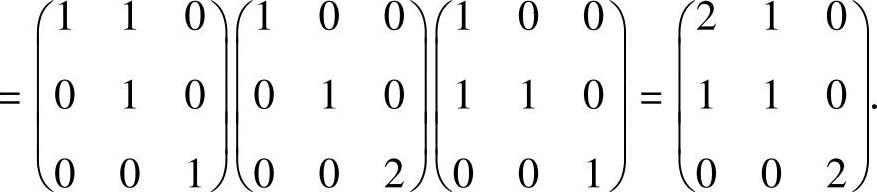
因此本题选(A).
附注 由于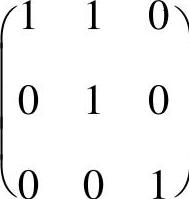 和
和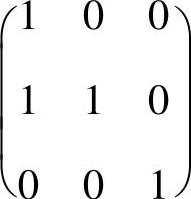 都是初等矩阵,所以以上的矩阵运算都可以简单地得到:
都是初等矩阵,所以以上的矩阵运算都可以简单地得到:

同样,
(7)分析 事件A与事件B互不相容,即AB=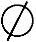 ,由此入手选择正确选项.
,由此入手选择正确选项.
精解 由AB=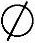 知
知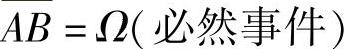 ,即
,即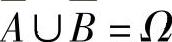 ,所以有
,所以有
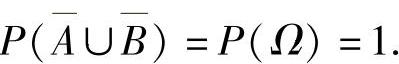
因此本题选(D).
附注 设A,B都是事件,则有
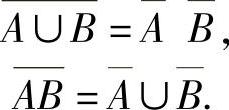
应记住这两个公式.
(8)分析 按分布函数的定义算出随机变量Z的分布函数FZ(z)后,即可确定间断点的个数.
精解 
由此可知,FZ(z)只有一个间断点z=0.
因此本题选(B).
附注 对于题中的随机变量X与Y,同样可以考虑FU(u)的间断点,其中FU(u)是随机变量U=X+Y的分布函数.
二、填空题
(9)分析 所给极限是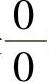 型未定式极限,先用等价无穷小代替化简后计算.
型未定式极限,先用等价无穷小代替化简后计算.
精解 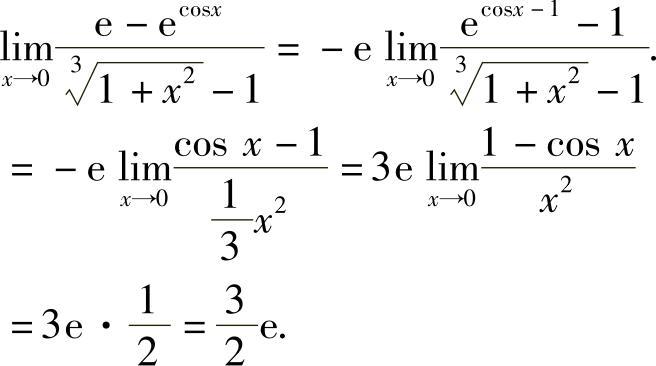
附注 计算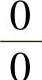 型未定式极限时,应先进行化简,其中等价无穷小代替是化简的主要手段.
型未定式极限时,应先进行化简,其中等价无穷小代替是化简的主要手段.
(10)分析 将y=0代入函数z的表达式,记所得函数为φ(x),然后计算φ′(1)即可.
精解 记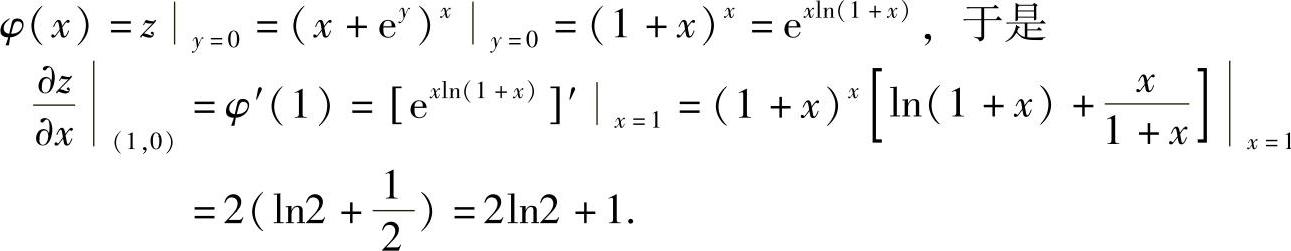
附注 本题也可以先求偏导数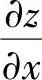 ,然后用x=1,y=0代入.但这样计算没有用题解中的方法快捷.
,然后用x=1,y=0代入.但这样计算没有用题解中的方法快捷.
(11)分析 设幂级数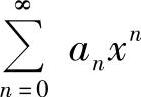 ,则它的收敛半径
,则它的收敛半径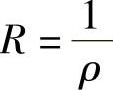 ,其中
,其中
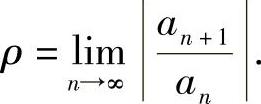
精解 记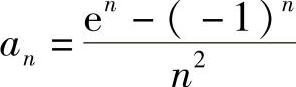 ,则
,则
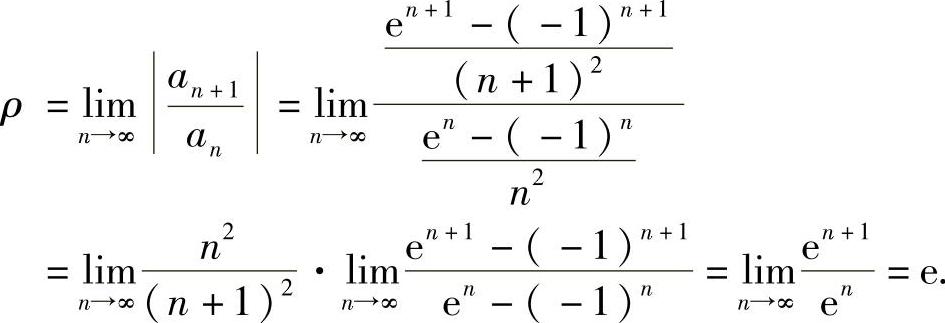
所以所给幂级数的收敛半径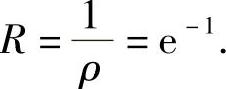
附注 幂级数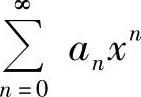 的收敛半径R的计算方法是:
的收敛半径R的计算方法是:
(ⅰ)如果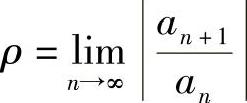 存在或为无穷大,则
存在或为无穷大,则
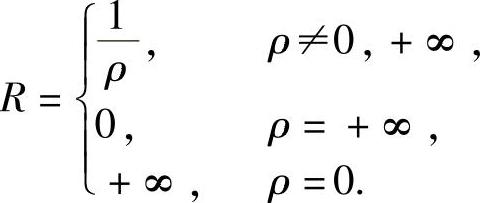
(ⅱ)如果数列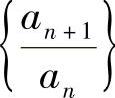 不存在(例如,
不存在(例如,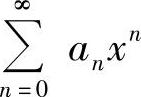 是缺项幂级数),或者虽然
是缺项幂级数),或者虽然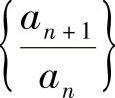 存在,但极限
存在,但极限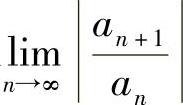 不存在且不为无穷大,此时把
不存在且不为无穷大,此时把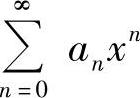 理解为
理解为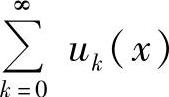 (其中uk(x)≠0,k=0,1,2,…),然后计算
(其中uk(x)≠0,k=0,1,2,…),然后计算
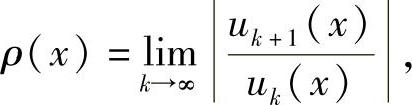
则收敛半径R可从(-R,R)={xρ(x)<1}算得.
(12)分析 收益函数L=Qp,因此只要计算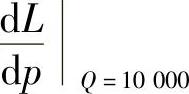 即可.
即可.
精解 由L=Qp得

由于 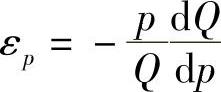 ,即
,即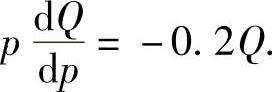
将它代入式(1)得
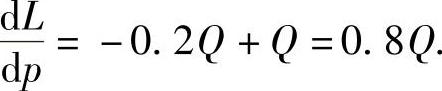
于是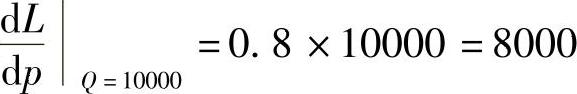 ,即当需求量为10000件时,价格增加1元,会使产品收益增加8000元.
,即当需求量为10000件时,价格增加1元,会使产品收益增加8000元.
附注 题解中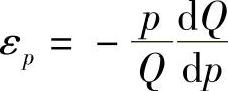 ,这是因为Q(p)是p的减函数,即
,这是因为Q(p)是p的减函数,即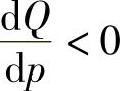 ,所以为了保证εp>0,故在公式右边加“-”号。
,所以为了保证εp>0,故在公式右边加“-”号。
(13)分析 利用相似矩阵的迹相等计算k的值.精解 αβT,即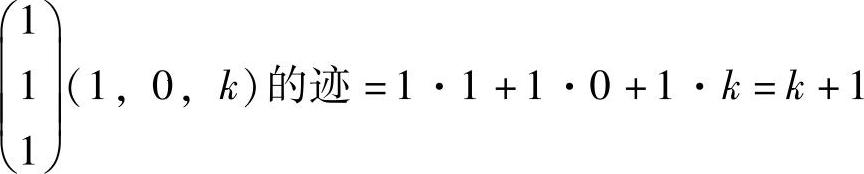 ,而
,而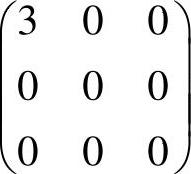 的迹为3+0+0=3.
的迹为3+0+0=3.
由于上述两个矩阵相似,所以它们的迹相等,即k+1=3,因此k=2.
附注 相似矩阵的以下性质是常用的:
设A~B,则trA=trB,|A|=|B|.
(14)分析 利用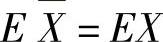 ,ES2=DX(其中X是总体)计算ET.
,ES2=DX(其中X是总体)计算ET.
精解 
由于X~B(n,p),所以EX=np,DX=np(1-p).将它们代入式(1)得
ET=np-np(1-p)=np2.
附注 要记住以下的结论:
设X1,X2,…,Xn是来自总体X(它的数学期望与方差分别为μ,σ2)的简单随机样本,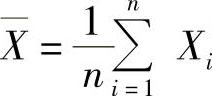 ,
,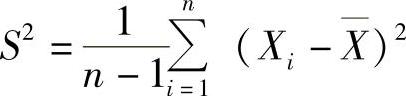 ,则
,则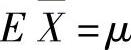 ,
,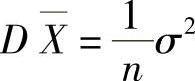 ,
,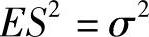 .
.
三、解答题
(15)分析 先计算二元函数f(x,y)的驻点,然后判断各个驻点是否为极值点,并计算极值点处的函数值(即极值).
精解 二元函数f(x,y)的定义域为上半平面y>0,在其中f(x,y)具有二阶连续偏导数,且
fx′=2x(2+y2),fy′=2x2y+1+lny,
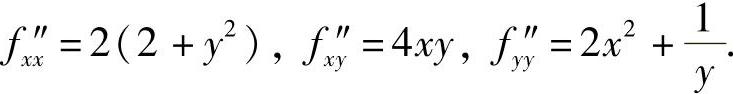
由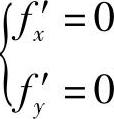
,
{,即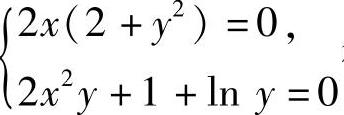 得x=0,
得x=0,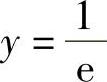 (它们是f(x,y)的唯一驻点).
(它们是f(x,y)的唯一驻点).
由于
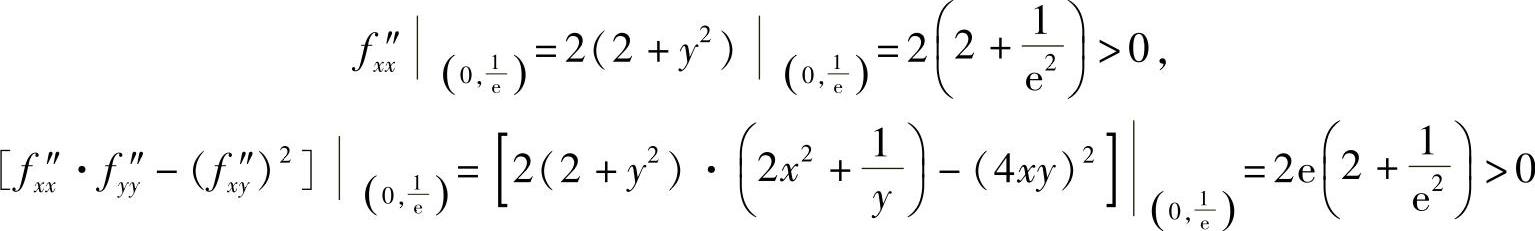
所以二元函数f(x,y)有极小值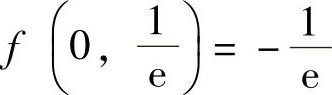 ,无极大值.
,无极大值.
附注 应熟练掌握二元函数极值的计算方法.
本题的有关内容与计算方法见提高篇11.
(16)分析 由于被积函数中有无理式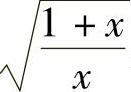 ,所以先用换元积分法,再考虑应用分部积分法计算所给的不定积分.
,所以先用换元积分法,再考虑应用分部积分法计算所给的不定积分.
精解 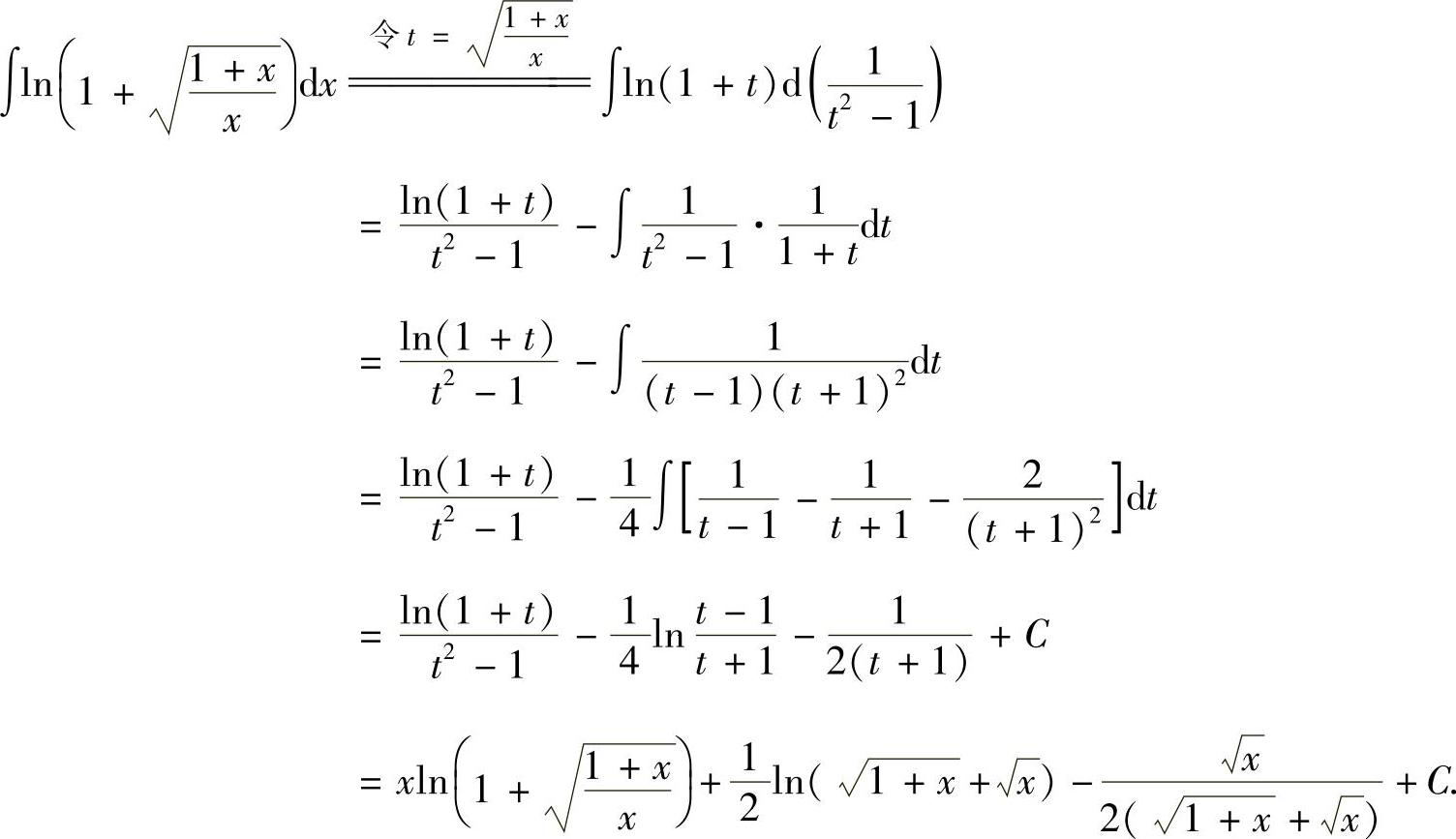
附注 题解中的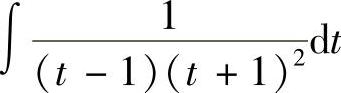 是有理函数的不定积分,其中被积函数的部分分式是按
是有理函数的不定积分,其中被积函数的部分分式是按
以下方法得到的:
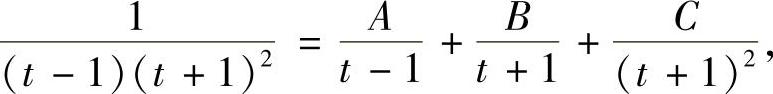
上式右边通分得
A(t+1)2+B(t-1)(t+1)+C(t-1)=1,(https://www.daowen.com)
即
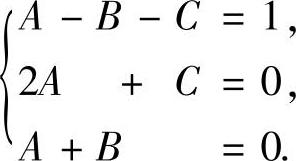
所以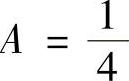 ,
,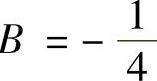 ,
,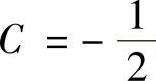 .从而
.从而
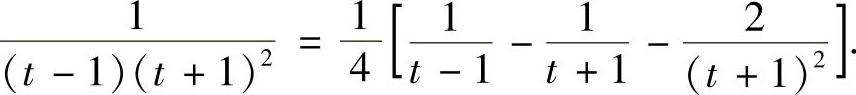
要熟练掌握有理真分式化成部分分式的方法.
(17)分析 由于D是角域(即从原点出发的半直线y=x,y=-x(y≥0)之间的区域)的一部分,所以采用极坐标计算所给的二重积分.
精解 由于D的极坐标表示式为
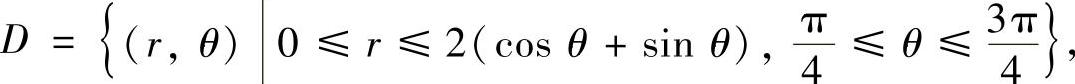
所以
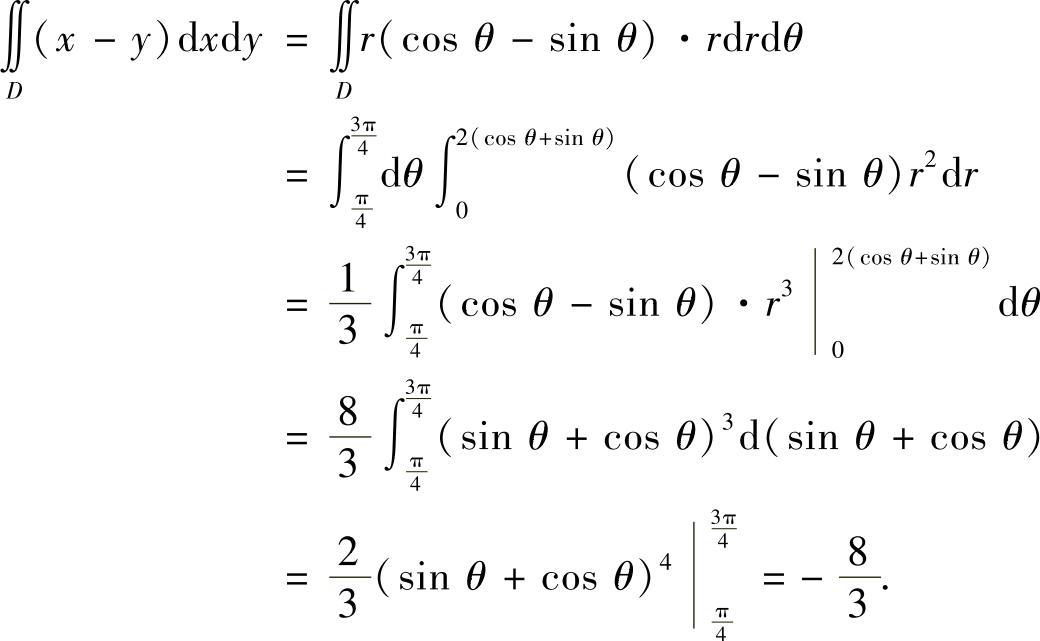
附注 题解中的极坐标系的极点取为原点,极轴取为x轴的正半轴,此时同一个点(x,y)与(r,θ)之间有
x=rcosθ,y=rsinθ.
现在将极坐标系的极点取为点(1,1),取由点(1,1)出发平行于x轴的半直线(方向与x轴的正半轴相同)为极轴,此时同一个点(x,y)与(ρ,φ)之间有
x=1+ρcosφ,y=1+ρsinφ.
现在在此坐标系下计算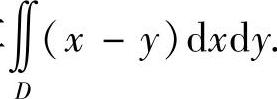
首先此时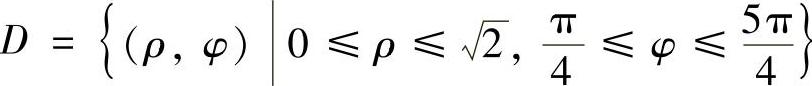 ,并且dxdy=ρdρdφ,所以
,并且dxdy=ρdρdφ,所以
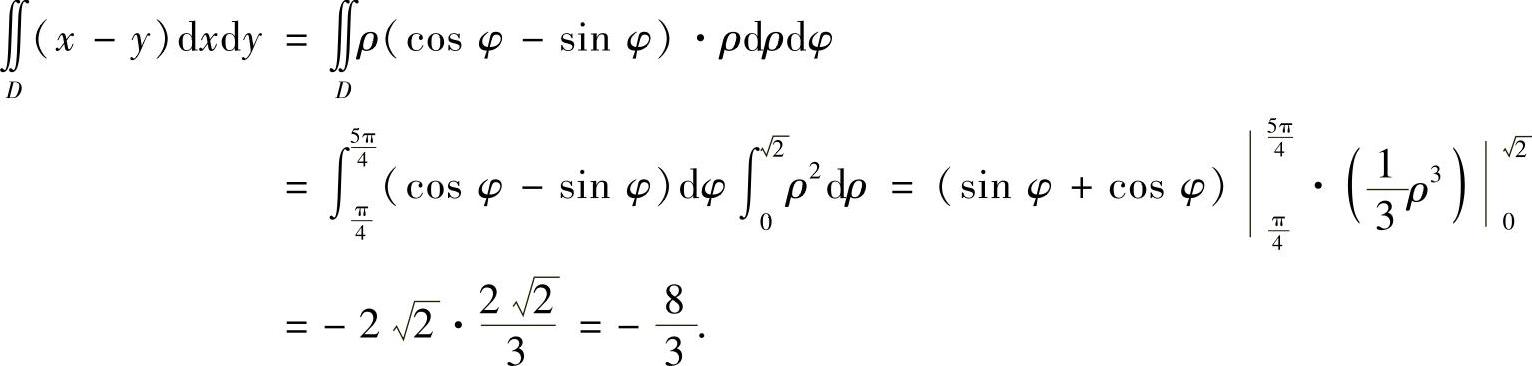
本题的有关计算方法见提高篇12.
(18)分析 (Ⅰ)作辅助函数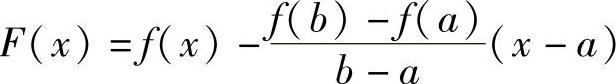 ,并对它在[a,b]上应用罗尔定理即可.
,并对它在[a,b]上应用罗尔定理即可.
(Ⅱ)利用拉格朗日中值定理,按右导数定义证明f′+(0)存在且为A.
精解 (Ⅰ)记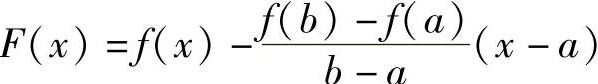 ,则函数F(x)在[a,b]上连续,在(a,b)内可导,且F(a)=F(b)(=f(a)),所以由罗尔定理知,存在ξ∈(a,b),使得F′(ξ)=0,即
,则函数F(x)在[a,b]上连续,在(a,b)内可导,且F(a)=F(b)(=f(a)),所以由罗尔定理知,存在ξ∈(a,b),使得F′(ξ)=0,即
f(b)-f(a)=f′(ξ)(b-a).
(Ⅱ)由题设知,对任意x∈(0,δ),f(t)在[0,x]上连续,在(0,x)内可导,所以由拉格朗日中值定理知,存在ξ∈(0,x),使得
f(x)-f(0)=f′(ξ)(x-0),即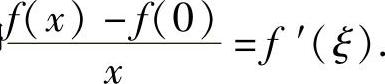
由于x→0+时,ξ→0+,所以
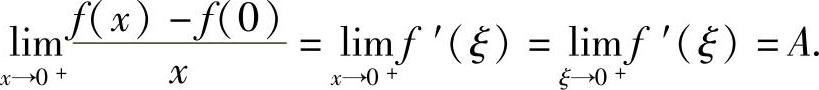
由此可知,f+′(0)存在且为A.
附注 本题(Ⅱ)可以推广为:
设函数f(x)在点x=c处连续,在(c,c+δ)(δ>0)内可导,且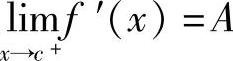 ,则f′ +(c)=A;
,则f′ +(c)=A;
设函数f(x)在点x=c处连续,在(c-δ,c)(δ>0)内可导,且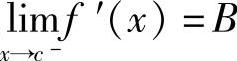 ,则f′ -(c)=B.这一推广有以下应用:
,则f′ -(c)=B.这一推广有以下应用:
设分段函数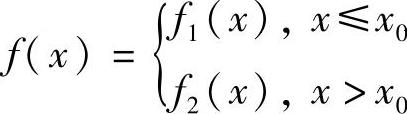
,
{,其中f(x)在点x=x0处连续,f1(x)(x<x0)可导,f2(x)(x>x0)可导.当已算得f′1(x)(x<x0)和f2′(x)(x>x0)时,f(x)在点x0处的可导性可按以下方法判别:
如果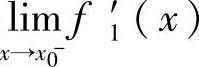 和
和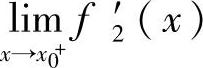 都存在且相等,则f(x)在点x0处可导,且
都存在且相等,则f(x)在点x0处可导,且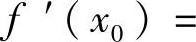
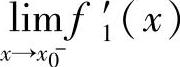 (或
(或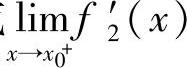 ).
).
本题(Ⅱ)的有关证明方法见提高篇04.
(19)分析 先算出曲边梯形面积和旋转体体积,由题设建立方程,然后求导将它转换成微分方程,求解此微分方程可得曲线方程y=f(x).
精解 曲边梯形面积为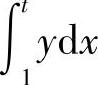 ,旋转体体积为
,旋转体体积为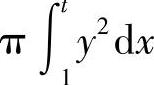 .于是由题设得
.于是由题设得
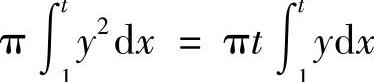 ,即
,即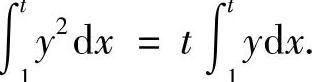
上式两边对t求导得

式(1)两边对t求导得
2yy′=2y+ty′,即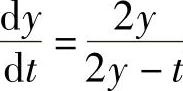 或
或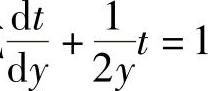 (一阶线性微分方程).
(一阶线性微分方程).
它的通解为
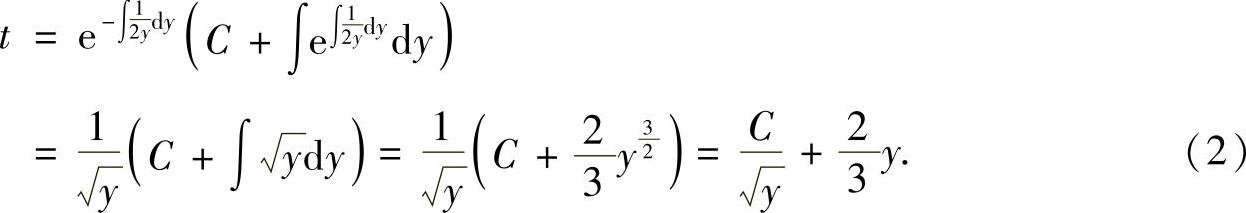
由式(1)可知,t=1时,y=1,0.由题设y>0,所以y=0应舍去,因此y|t=1=1.将它代入式(2)得
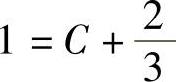 ,即
,即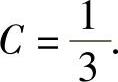
将它代入式(2)得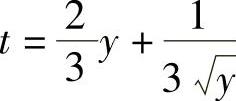 ,即
,即

由于当x>1时,y>1,从而由式(3)知
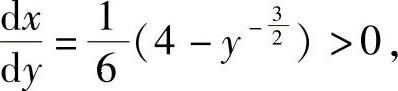
因此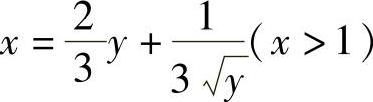 的反函数存在,记为y=f(x),它即为所求的曲线方程.
的反函数存在,记为y=f(x),它即为所求的曲线方程.
附注 (ⅰ)实际上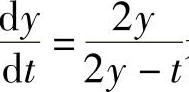 是齐次方程,其通解可直接计算如下:
是齐次方程,其通解可直接计算如下:
令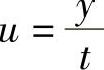 ,则所给微分方程成为
,则所给微分方程成为
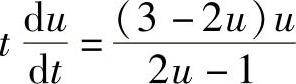 ,即
,即 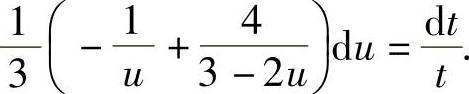
上式两边分别积分得
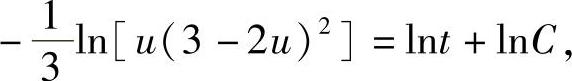
即
u(3-2u)2=(Ct)-3
由y|t=1=1知u|t=1=1,将它代入上式得C=1.再将C=1代入上式得
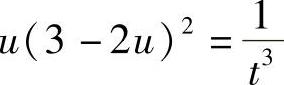 ,即y(3t-2y)2=1或
,即y(3t-2y)2=1或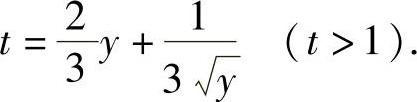
(ⅱ)题解中算出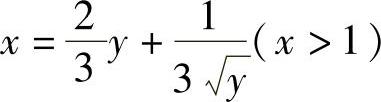 后,其反函数才是所求的曲线方程.因此有必要说明这个反函数是存在的,这就是题解中最后部分所做的工作.
后,其反函数才是所求的曲线方程.因此有必要说明这个反函数是存在的,这就是题解中最后部分所做的工作.
本题是综合题,其有关内容与计算方法见提高篇09,15.
(20)分析 (Ⅰ)解非齐次线性方程组算得所有的ξ2,ξ3.
(Ⅱ)计算(ξ1,ξ2,ξ3)的行列式,判定ξ1,ξ2,ξ3线性无关.
精解(Ⅰ)对增广矩阵(A┆ξ1)施行初等行变换:

记ξ2=(x1,x2,x3)T,则方程组Aξ2=ξ1与方程组

同解,式(1)对应的导出组的基础解系为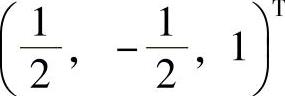 ,式(1)有特解
,式(1)有特解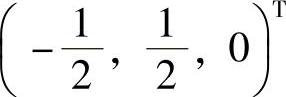 ,所以
,所以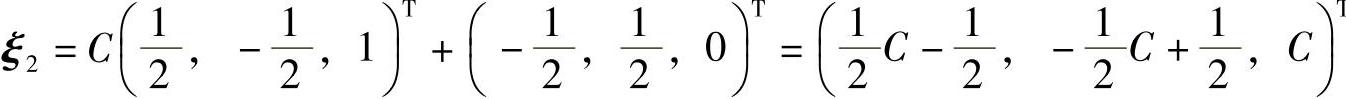 (C为任意常数).
(C为任意常数).
由于
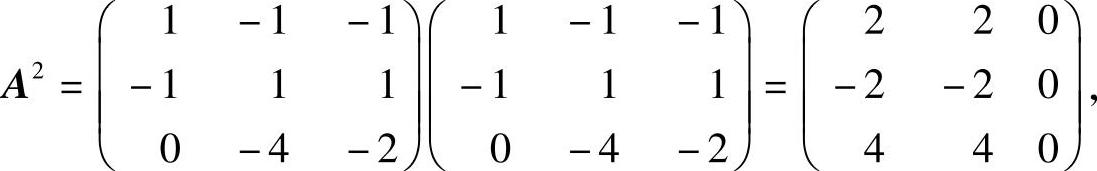
对增广矩阵(A2┆ξ1)施行初等行变换:
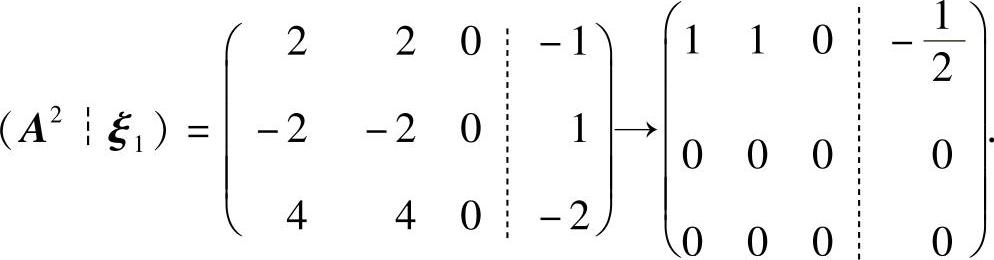
记ξ3=(y1,y2,y3)T,则方程组A2ξ3=ξ1与方程

同解,式(2)对应的导出组的基础解系为(-1,1,0)T和(0,0,1)T,式(2)有特解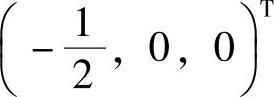 ,所以
,所以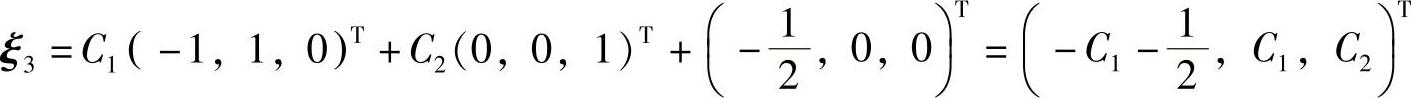 (C1,C2是任意常数).
(C1,C2是任意常数).
(Ⅱ)因为对于任意C,C1,C2有
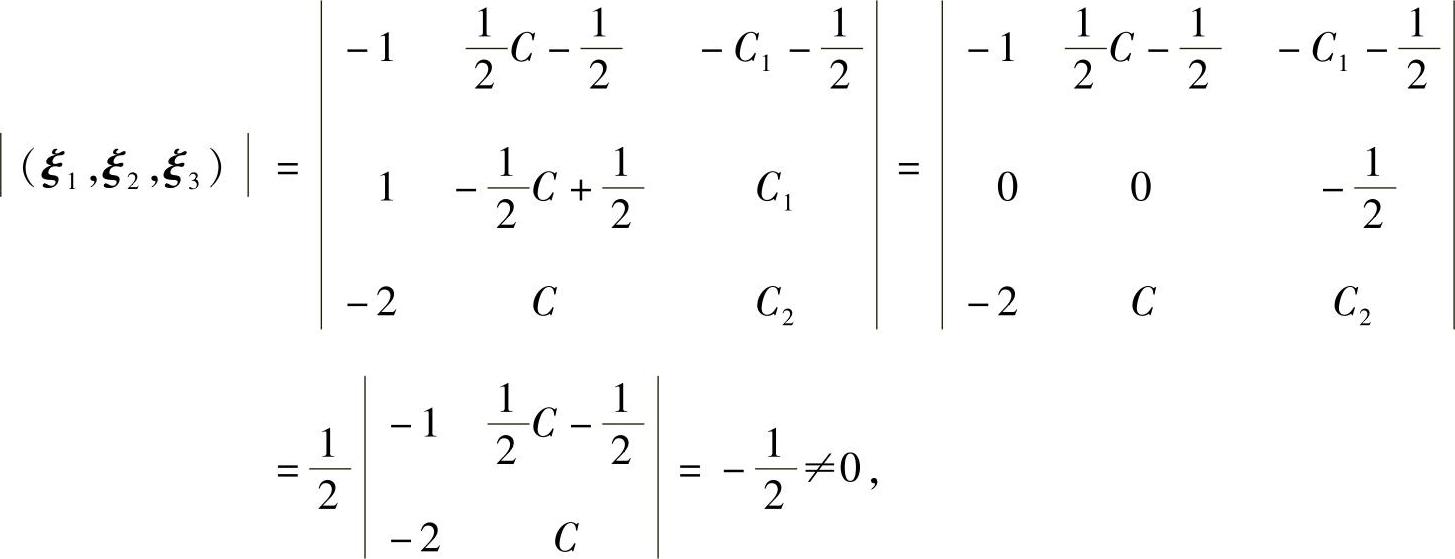
所以,向量组ξ1,ξ2,ξ3线性无关.
附注 (ⅰ)应熟练掌握非齐次线性方程组的通解计算方法.
(ⅱ)要判定n个n维列向量α1,α2,…,αn的线性相关性,如果这n个向量的元素是具体的数字或文字,其快捷方法是构造矩阵A=(α1,α2,…,αn),当|A|≠0时,α1,α2,…,αn线性无关;当|A|=0时,α1,α2,…,αn线性相关.
本题是综合题,其有关内容及计算方法见提高篇18.
(21)分析 (Ⅰ)写出二次型f的矩阵A,然后由|λE-A|(E是三阶单位矩阵)算出A的所有特征值.
(Ⅱ)令矩阵A的最小特征值为零,即得a的值.
精解 (Ⅰ)二次型f的矩阵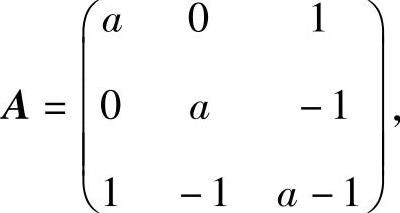
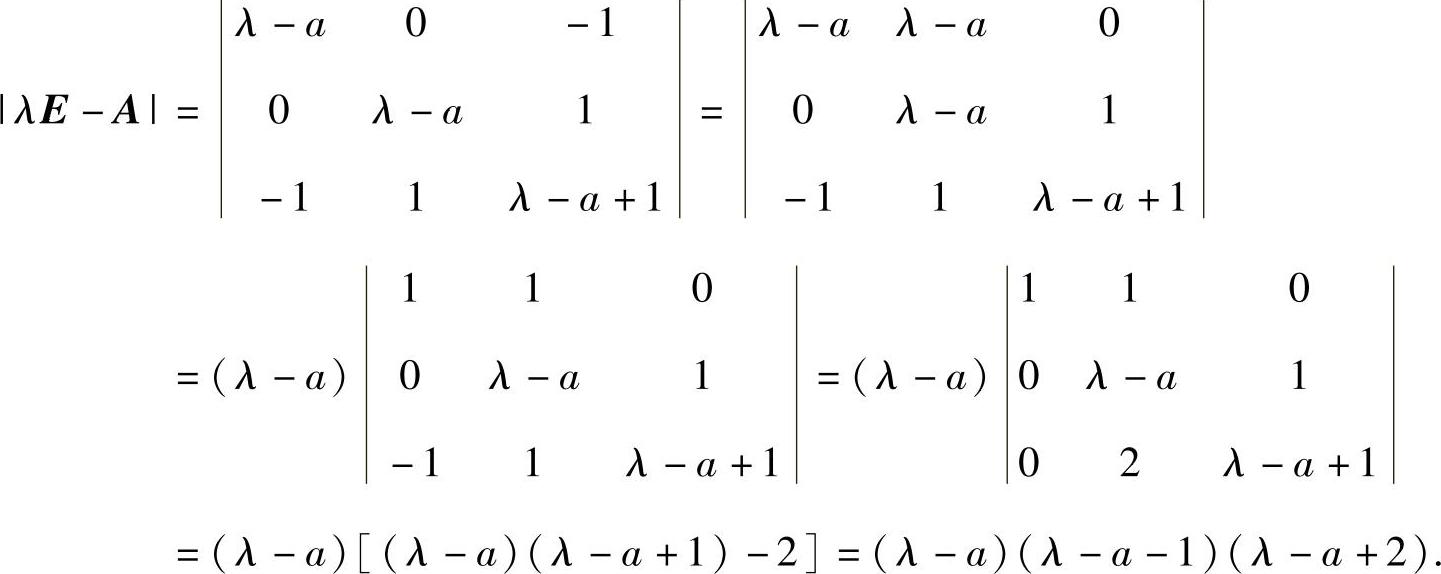
由此知矩阵A有特征值a-2,a,a+1(由小到大排列).
(Ⅱ)由二次型f的规范形为y21+y22知矩阵A的正惯性指数为2,负惯性指数为0,所以矩阵A有两个正特征值和一个零特征值.从而a-2=0,即a=2.
附注 二次型f(x1,x2,…,xn)=xTAx(其中x=(x1,x2,…,xn)T,A是实对称矩阵)的规范形是唯一的,即其中的正平方项个数p(正惯性指数)与负平方项个数q(负惯性指数)由f唯一确定.
p即为实对称矩阵A的正特征值个数,q即为实对称矩阵A的负特征值个数.
本题是综合题,其有关内容及计算方法见提高篇19,20.
(22)分析 (Ⅰ)先算出关于随机变量X的边缘概率密度fX(x),然后按公式计算fY|X(y|x).
(Ⅱ)先算出关于随机变量Y的边缘概率密度,然后按条件概率计算公式计算概率P(X≤1|Y≤1).
精解 (Ⅰ)由题设知,函数f(x,y)仅在图B.09.1的
阴影部分取值为e-x,在xOy平面的其他部分都取值为0,所以二维随机变量(X,Y)的关于X的边缘概率密度
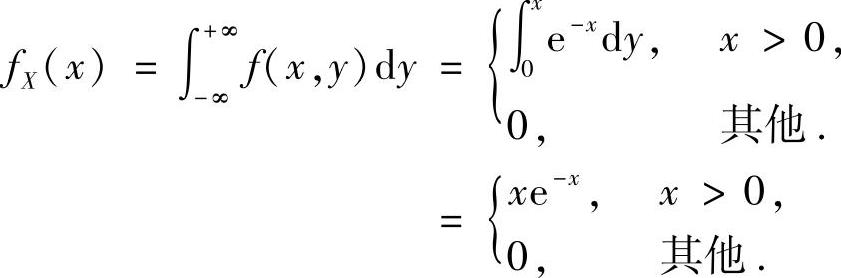
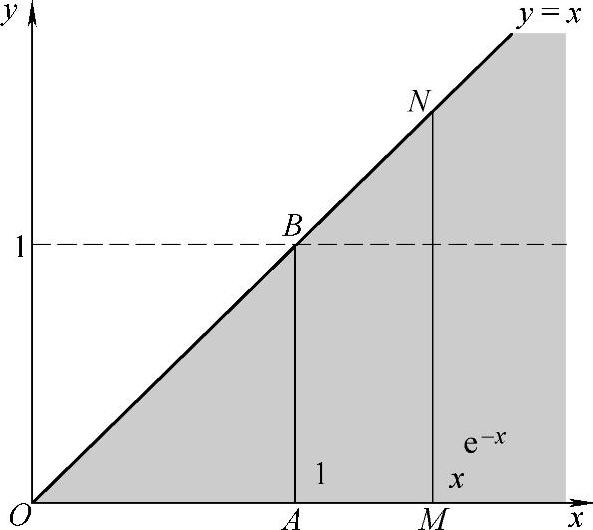
图 B.09.1
显然,仅在(0,+∞)上fX(x)≠0,于是对于x∈(0,+∞)有
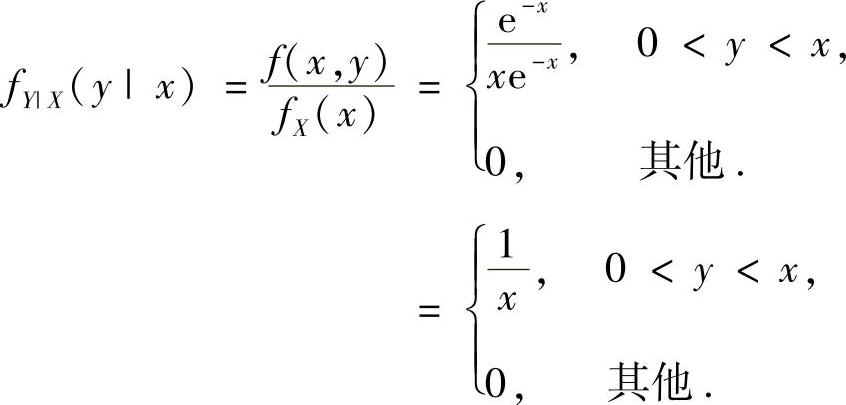
(Ⅱ)二维随机变量(X,Y)的关于Y的边缘概率密度
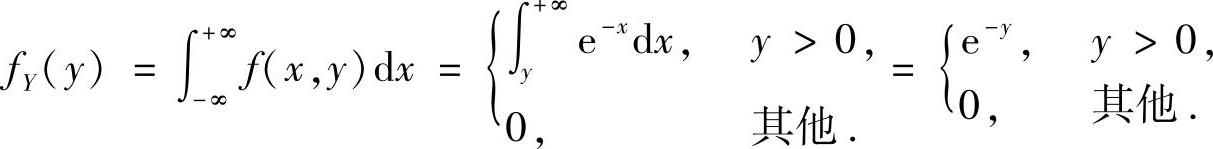
所以,
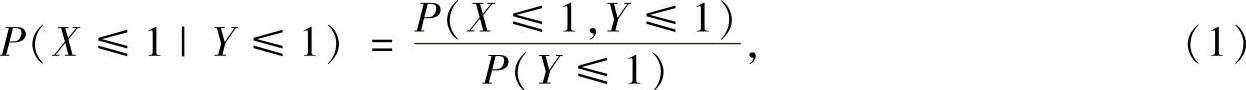
其中,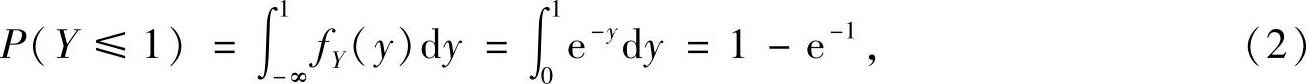
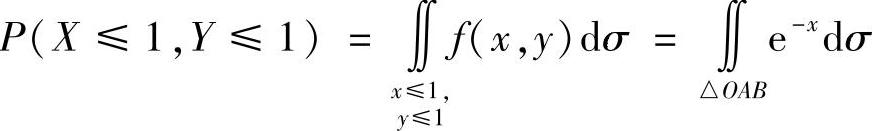
(△OAB如图B.09.1所示,其中A=(1,0),B=(1,1))
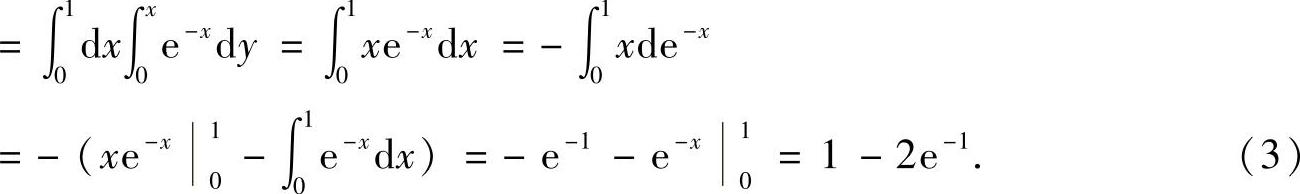
将式(2)、式(3)代入式(1)得
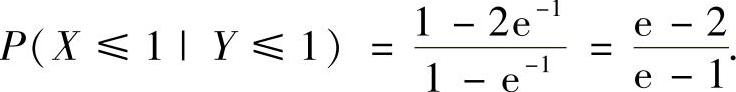
附注 由二维随机变量的概率密度f(x,y)计算关于X的边缘概率密度时,应注意积分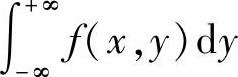 是对于任意固定的x∈(-∞,+∞)计算的,即这个积分是沿横坐标为x的铅垂直线计算的.由图B.09.1可知,当x≤0时,f(x,y)在这条铅垂直线上取值均为零,因此有
是对于任意固定的x∈(-∞,+∞)计算的,即这个积分是沿横坐标为x的铅垂直线计算的.由图B.09.1可知,当x≤0时,f(x,y)在这条铅垂直线上取值均为零,因此有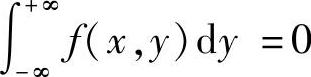 ;当x>0时,f(x,y)在这条铅垂直线位于阴影部分(即该图中所示的线段MN)上取值为e-x,在其余部分上取值均为零,因此有
;当x>0时,f(x,y)在这条铅垂直线位于阴影部分(即该图中所示的线段MN)上取值为e-x,在其余部分上取值均为零,因此有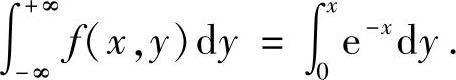
对于计算关于Y的边缘概率密度时的积分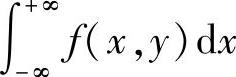 有同样的说法.
有同样的说法.
进一步深入学习见提高篇23.
(23)分析 (Ⅰ)用条件概率公式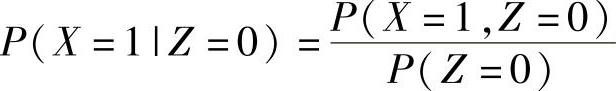 计算概率P(X=1|Z=0).
计算概率P(X=1|Z=0).
(Ⅱ)先确定二维随机变量(X,Y)所有可能取的值,然后计算(X,Y)取各个值的概率,即得(X,Y)的概率分布.
精解 (Ⅰ)由于
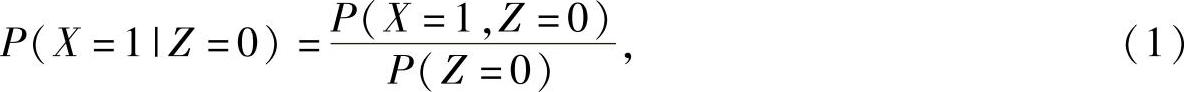
式中,
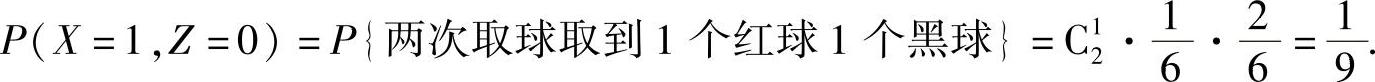
将它们代入式(1)得
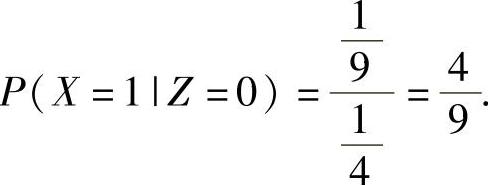
(Ⅱ)X,Y全部可能取的值都为0,1,2,且

P(X=2,Y=1)=P(X=2,Y=2)=0,
所以,二维随机变量(X,Y)的概率分布可表示如下:
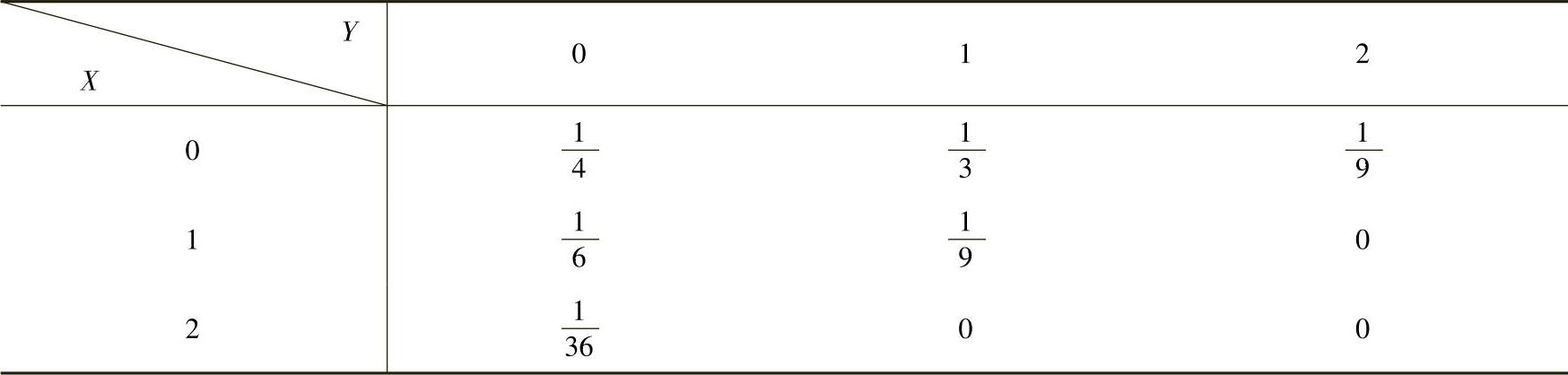
附注 计算二维离散型随机变量(X,Y)的概率分布的步骤如下:
(ⅰ)确定(X,Y)全部可能取的值;
(ⅱ)计算(X,Y)取各个值的概率,此时往往需用计算随机事件概率的各种方法.
本题的有关内容及计算方法见提高篇21.
