2014年全国硕士研究生入学统一考试试题解答
一、选择题
(1)分析 按数列极限定义选择正确的选项.
精解 由
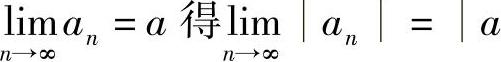 |,所以对
|,所以对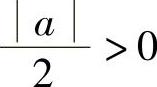 ,存在正整数N,使得当n>N时,
,存在正整数N,使得当n>N时,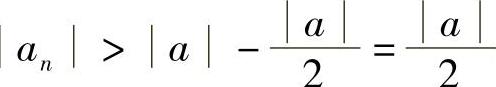 .
.
因此本题选(A).
附注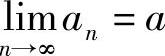 是
是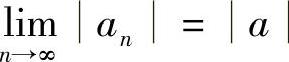 的充分而非必要条件.
的充分而非必要条件.
(2)分析 从计算非铅直渐近线入手
精解 对选项(C),由于
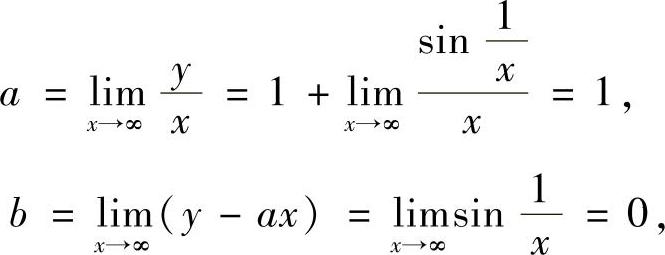
所以,曲线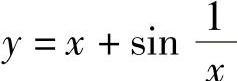 有渐近线y=x.
有渐近线y=x.
因此本题选(C).
附注 对于曲线y=y(x),如果极限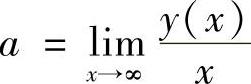 与
与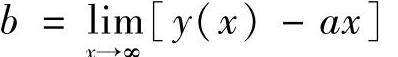
都存在,则该曲线有非铅直渐近线.
(3)分析 由题设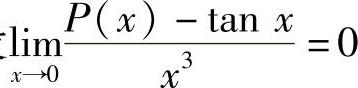 计算a,b,c,d的取值.
计算a,b,c,d的取值.
精解 由题设P(x)-tanx=a+bx+cx2+dx3-tan x是x3的高阶无穷小知
tan x=a+bx+cx2+dx3-o(x3) (x→0).
由此得到 a=tanx|x=0=0,
b=(tanx)′|x=0=sec2x|x=0=1,
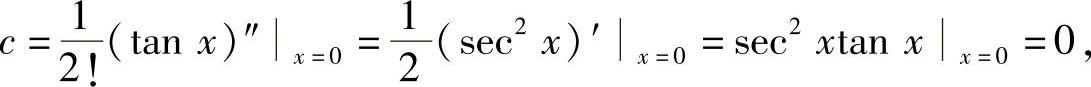
所以选项(A)、(B)、(C)都是正确的.
因此本题选(D).
附注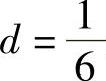 是错误的,这是因为
是错误的,这是因为
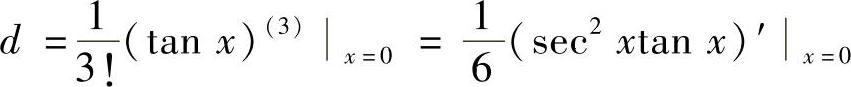
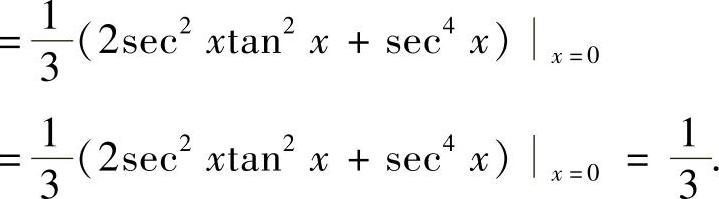
(4)分析 利用f(x)在[0,x]与[x,1](x∈(0,1))上的拉格朗日中值定理证明.
精解 对x∈(0,1)时,由
f(x)=f(0)+f′(ξ1)x (ξ1∈(0,x)),
f(x)=f(1)-f′(ξ2)(1-x) (ξ2∈(x,1))
得 f(x)=f(0)(1-x)+f(1)x+[f′(ξ1)-f′(ξ2)]x(1-x)
=g(x)-f″(η)(ξ2-ξ1)x(1-x) (η∈(ξ1,ξ2)⊂(0,1)).
于是,当f″(x)≤0(x∈(0,1))时,有f(x)≥g(x)(x∈(0,1)).此外,f(0)=g(0),f(1)=g(1).所以有
f(x)≥g(x) (x∈[0,1]).
因此本题选(C).
附注 当f″(x)<0(x∈[0,1])时,f(x)≥g(x)(x∈[0,1]),且仅在点x=0,1处取等号.
当f″(x)≤0(x∈[0,1])时,f(x)≥g(x)(x∈[0,1]),但是取等号的点未必限于点x=0与x=1.
(5)分析 按第一行展开即可.
精解 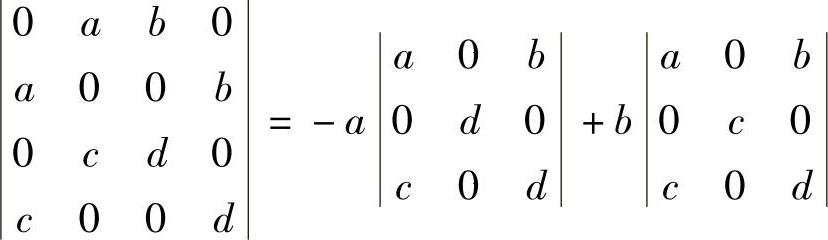
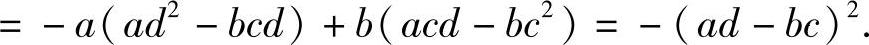
因此本题选(B).
附注 本题可按任一行(列)展开计算.
(6)分析 按向量组线性无关定义进行推理.
精解 设α1,α2,α3线性无关,则对常数λ1,λ2有
λ1(α1+kα3)+λ2(α2+lα3)=0,即λ1α1+λ2α2+(λ1k+λ2l)α3=0时,必有λ1=λ2=0.由此可知α1+kα3,α2+lα3线性无关.
但反之未必成立,例如α1=(1,0,0)T,α2=(0,1,0)T,α3=(0,0,0)T,则α1+kα3=α1,α2+lα3=α2线性无关,但α1,α2,α3线性相关.
因此本题选(A).
附注 本题的必要性也可证明如下:
设α1,α2,α3是线性无关的三维列向量组,则由
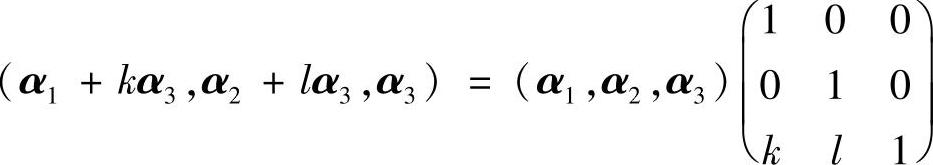
及矩阵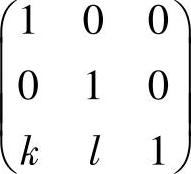 可逆知,α1+kα3,α2+lα3,α3线性无关,从而α1+kα3,α2+lα3线性无关.
可逆知,α1+kα3,α2+lα3,α3线性无关,从而α1+kα3,α2+lα3线性无关.
(7)分析 利用随机事件概率计算公式,先算出P(A),再计算P(B-A).
精解 由0.3=P(A-B)=P(A)-P(AB)=P(A)-P(A)P(B)
=P(A)(1-P(B))=0.5P(A)
得P(A)=0.6,所以
P(B-A)=P(B)-P(AB)=P(B)-P(B)P(A)=0.5-0.5×0.6=0.2.
因此本题选(B).
附注 随机事件的减法公式是
P(A-B)=P(A)-P(AB),
当B⊆A时,P(A-B)=P(A)-P(B).
(8)分析 先分别确定X1-X2,|X3|服从的分布,然后确定S服从的分布.
精解 由于X1,X2都服从N(0,σ2)且它们相互独立,所以由X1-X2~N(0,2σ2)知,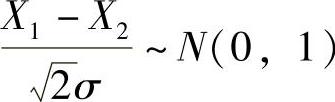 .此外,由X3~N(0,σ2)知
.此外,由X3~N(0,σ2)知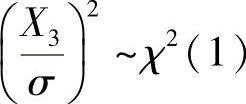 ,以及
,以及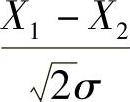 与
与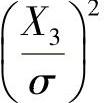 相互独立知
相互独立知
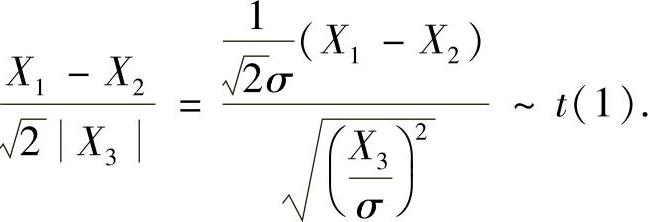
因此本题选(C).
附注 常用的抽样分布χ2(n),t(n)以及F(n1,n2)的定义如下:
(Ⅰ)设随机变量X1,X2,…,Xn相互独立,且都服从N(0,1),则随机变量Y=X21+X22+…+X2n所服从的分布称为自由度为n的χ2分布,记为χ2(n).
(Ⅱ)设随机变量X~N(0,1),Y~χ2(n),且相互独立,则随机变量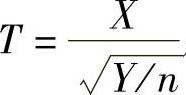 所服从的分布称为自由度为n的t分布,记为t(n).
所服从的分布称为自由度为n的t分布,记为t(n).
(Ⅲ)设随机变量X~χ2(n1),Y~χ2(n2),且相互独立,则随机变量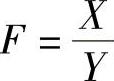 所服从的分布称为自由度为n1,n2的F分布,记为F(n1,n2).
所服从的分布称为自由度为n1,n2的F分布,记为F(n1,n2).
二、填空题
(9)分析 先写出收益函数,然后求导即得边际收益.
精解 收益R是需求量q的函数,即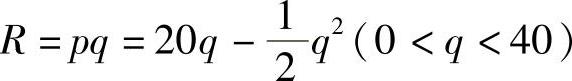 ,因此边际收益
,因此边际收益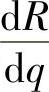
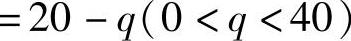
附注 顺便计算收益价格弹性.
由于收益关于价格的函数为
R=pq=40p-2p2 (0<p<20)
所以,收益价格弹性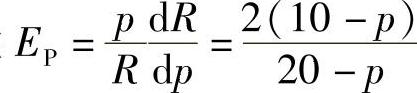 .
.
(10)分析 先画出D的图形,然后用定积分计算D的面积S.
精解 D如图B.14.1阴影部分所示,所以S=
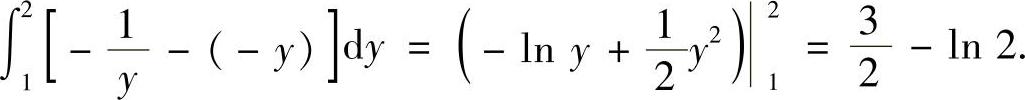
附注 S也可用二重积分计算,具体如下:
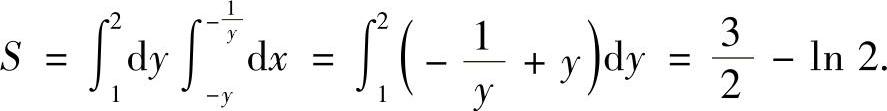
(11)分析 先算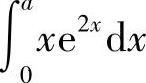 ,然后利用题设条件计算a的值.
,然后利用题设条件计算a的值.
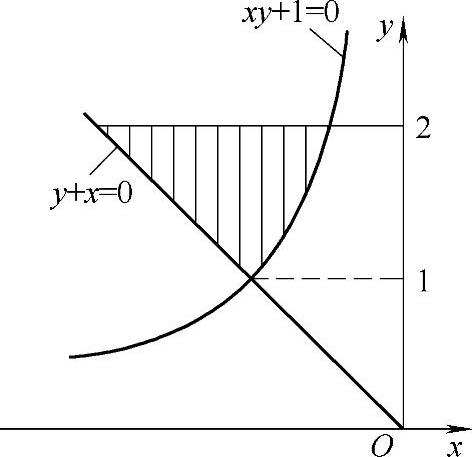
图 B.14.1
精解 由于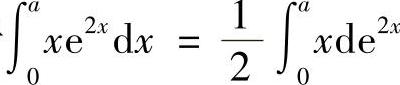
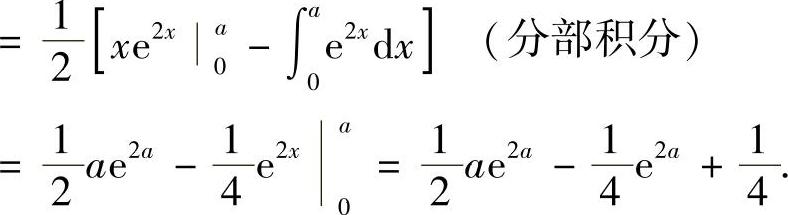
所以由题设条件得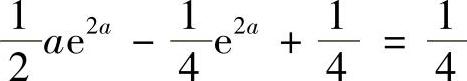 ,即(2a-1)e2a=0,
,即(2a-1)e2a=0,
因此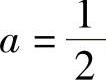 .
.
附注 以下问题难度比本题稍高:
设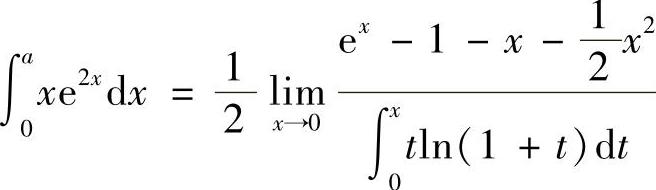 ,求a的值.
,求a的值.
其解答如下:
由于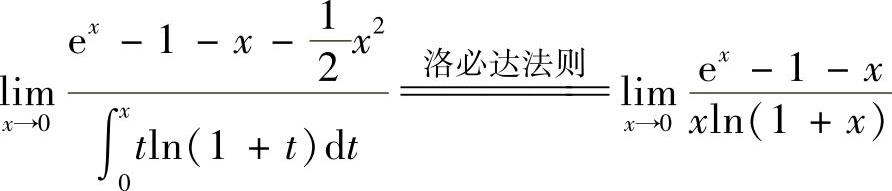

所以有 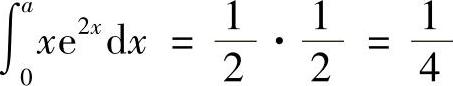 ,从而
,从而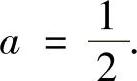
(12)分析 改变积分次序后即可算得这个二次积分的值.
精解 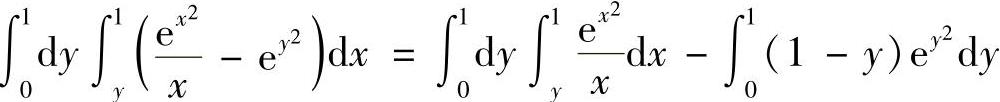
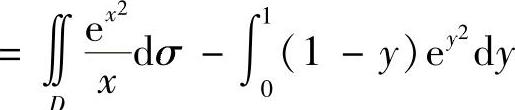
(D={(x,y)y≤x≤1,0≤y≤1}={(x,y)0≤y≤x,0≤x≤1}如图B.14.2阴影部分所示)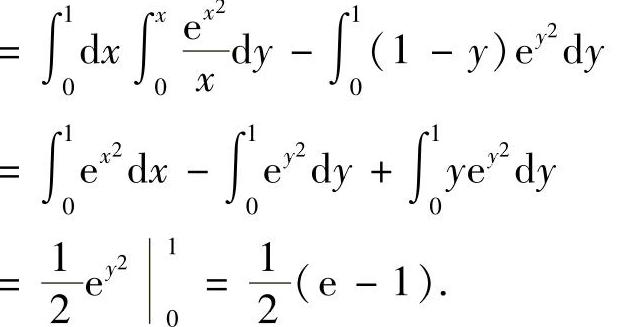
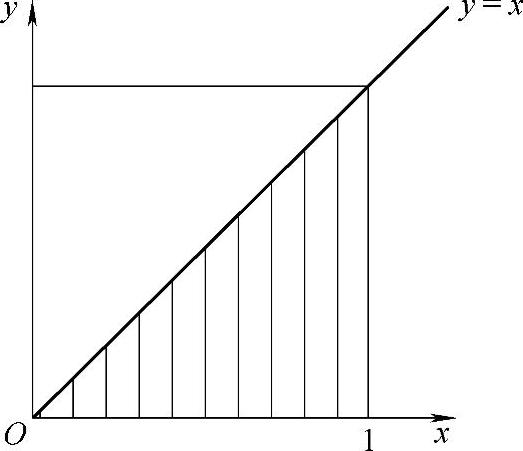
图 B.14.2
附注 本题的关键是计算∫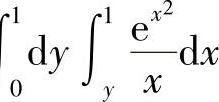 ,直接计算是不行的,故改变积分次序后再行计算.
,直接计算是不行的,故改变积分次序后再行计算.
(13)分析 用配平方方法将f(x1,x2,x3)转换成标准型,即可确定a的取值范围.
精解 由于
f(x1,x2,x3)=[x21+2ax1x3+(ax3)2]-[x21-4x2x3+(2x3)2]+(4-a2)x23
=(x1+ax3)2-(x1-2x3)2+(4-a)x23
=y21-y22+(4-a2)y23
(其中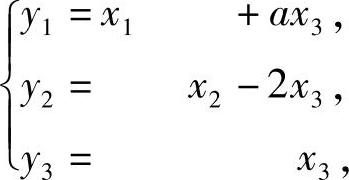 即
即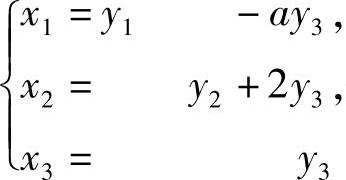 是可逆线性变换),所以当f(x1,x2,x3)的负惯性指数为1时,a应满足4-a2≥0,故a的取值范围为[-2,2].
是可逆线性变换),所以当f(x1,x2,x3)的负惯性指数为1时,a应满足4-a2≥0,故a的取值范围为[-2,2].
附注 对二次型f(x1,x2,x3)进行可逆线性变换,不改变其矩阵的秩,也不改变其正惯性指数(或负惯性指数)的值.
(14)分析 先算出E(X2),然后用统计量的无偏性的定义计算c.
精解 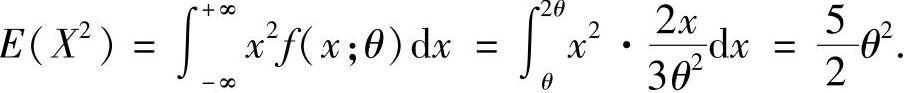
所以,由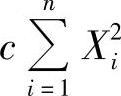 是θ2的无偏估计量得
是θ2的无偏估计量得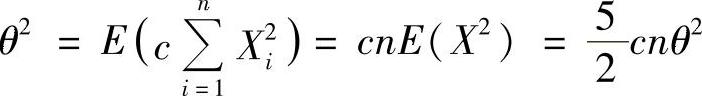 ,即
,即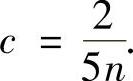
附注 评判总体X分布中的未知参数θ的估计量θ^的常用标准是:
(Ⅰ)无偏性 如果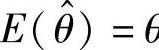 θ,则称
θ,则称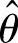 是θ的无偏估计量.
是θ的无偏估计量.
(Ⅱ)有效性 如果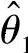 ,
,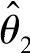 都是θ的无偏估计量,则当
都是θ的无偏估计量,则当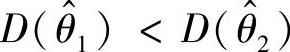 时,称
时,称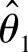 是较
是较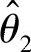 有效的估计量.
有效的估计量.
三、解答题
(15)分析 由于分子是积分上限函数,所以先用洛必达法则计算所给的未定式极限.
精解 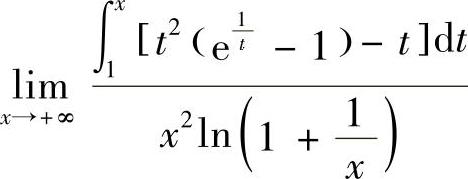
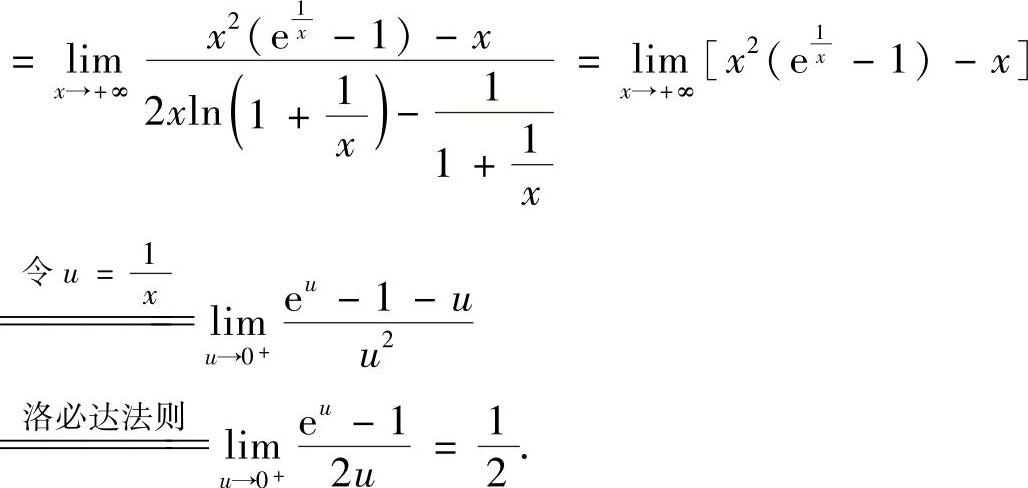
附注 本题也可用以下方法计算:

本题是 型未定式极限.在基础篇第二章六及提高篇01中可以找到与本题类似的例题.
型未定式极限.在基础篇第二章六及提高篇01中可以找到与本题类似的例题.
(16)分析 由于积分区域是角域的一部分,所以用极坐标计算所给的二重积分.
精解 
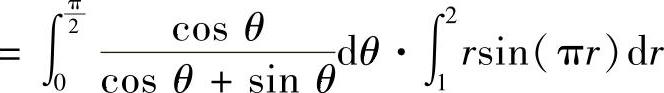
其中,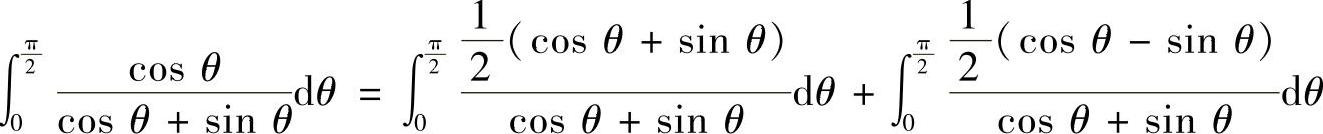
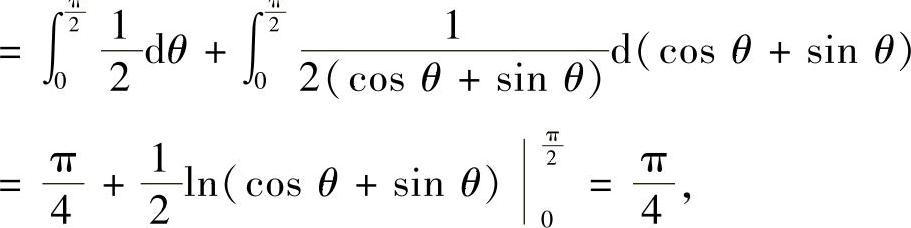
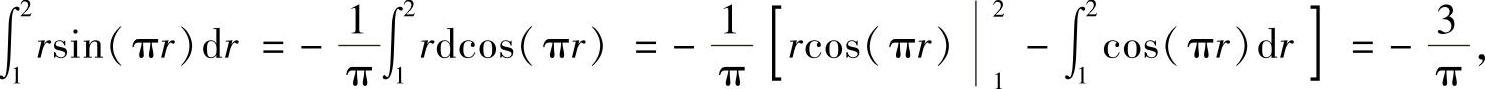
所以,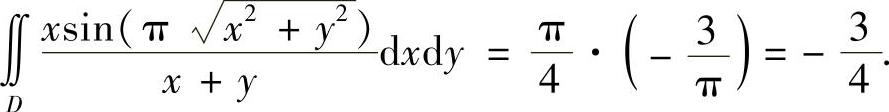
附注 当积分区域D是角域的一部分,即D={(r,θ)|r0≤r(θ)≤r1,0≤θ0≤θ≤θ1≤2π}时,通常用极坐标计算二重积分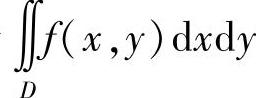 (其中f(x,y)在D及其边界上连续).
(其中f(x,y)在D及其边界上连续).
本题中使用的二重积分计算方法及例题可以从基础篇第三章八中找到.(https://www.daowen.com)
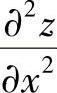 与
与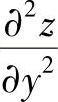 ,并利用它们满足的等式得到关于f(u)的微分方程,然后求解该微分方程得到f(u)的表达式.
,并利用它们满足的等式得到关于f(u)的微分方程,然后求解该微分方程得到f(u)的表达式.
精解 由dz=f′(u)[excosydx+(-exsiny)dy](其中u=excosy)
得 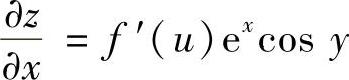 ,
,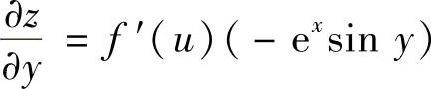 ,
,
所以,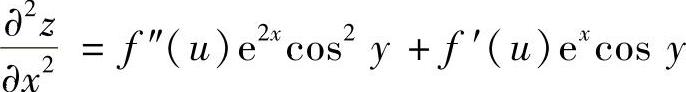 ,
,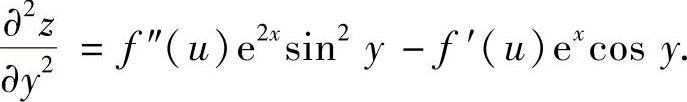
从而由所给等式得
f″(u)e2x=[4f(u)+u]e2x,
即 f″(u)-4f(u)=u.(二阶常系数非齐次线性微分方程) (1)
由于f″(u)-4f(u)=0有通解 F=C1e2x+C2e-2x,以及f″(u)-4f(u)=u有特解f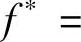
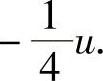 所以式(1)的通解为
所以式(1)的通解为
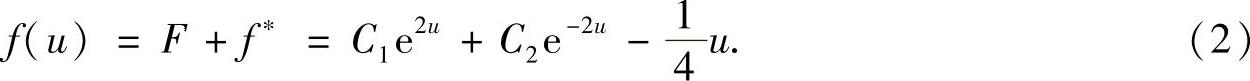
且 
将f(0)=f′(0)=0代入式(2)、式(3)得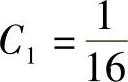 ,
,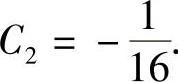 将它们代入式(2)得
将它们代入式(2)得
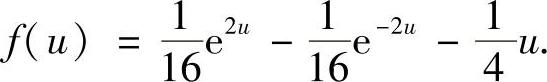
附注 本题是偏导数计算与求解二阶常系数线性微分方程的综合题,应熟练掌握一、二阶偏导数的计算和二阶常系数线性微分方程的解法.
在提高篇16中可以找到与本题十分相似的例题
(18)分析 先计算所给幂级数的收敛域,然后在收敛域内通过逐项微分算出和函数.
精解 记 an=(n+1)(n+3),则由
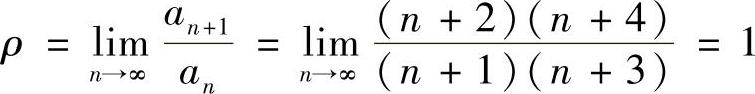
知所给幂级数的收敛半径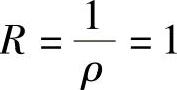 .此外,在点x=-1,1处所给幂级数都发散,所以收敛域为(-1,1).
.此外,在点x=-1,1处所给幂级数都发散,所以收敛域为(-1,1).
当x∈(-1,1)时,幂级数的和函数为
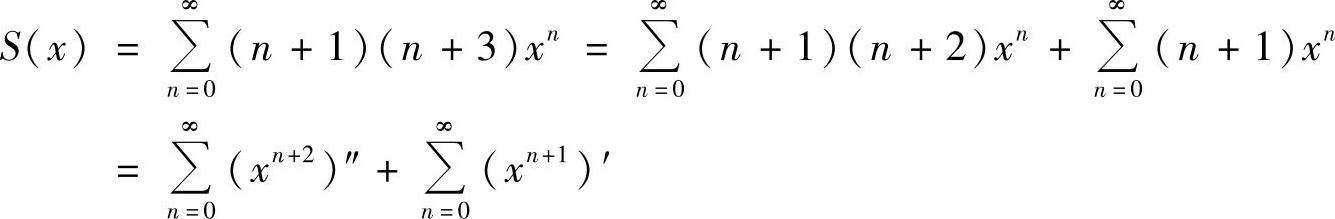
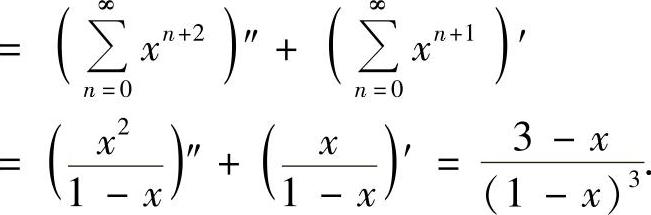
附注 题解中求和函数方法十分快捷,但也可以用以下方法计算:
当x∈(-1,0)∪(0,1)时,
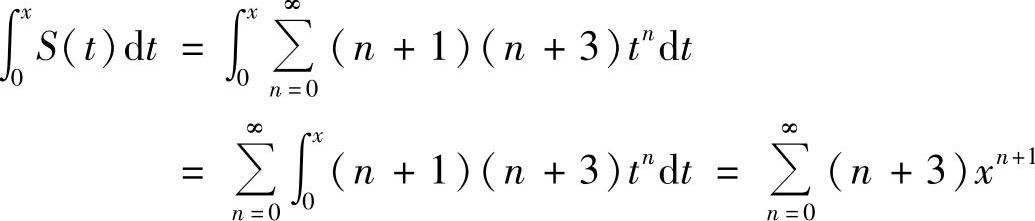
得 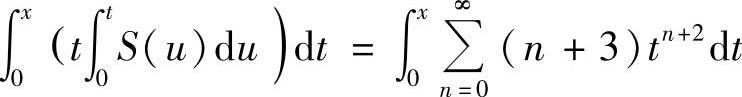
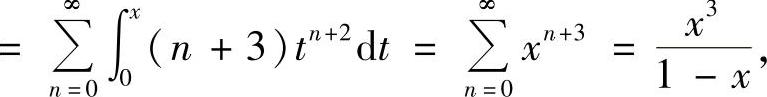
所以 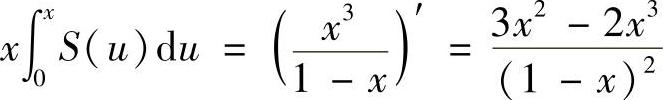 ,即
,即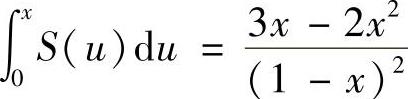 .
.
于是,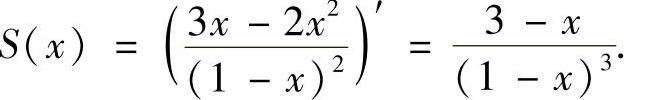
此外,S(0)=1·3=3.所以,
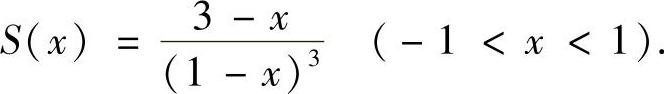
在提高篇13中可以找到与本题十分相似的例题.
(19)分析 (Ⅰ)可由0≤g(x)≤1直接得到.
(Ⅱ)将欲证不等式中的b换成x,然后用对变上限积分求导数的方法证明.
精得 (Ⅰ)对x∈[a,b],由0≤g(x)≤1得
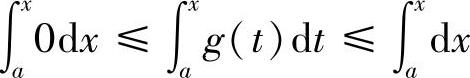
,即
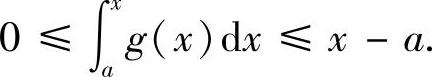
(Ⅱ)将欲证不等式中的b改为x,并记
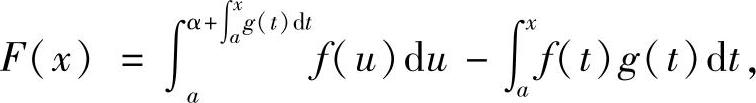
则F(x)在[a,b]上可导,且
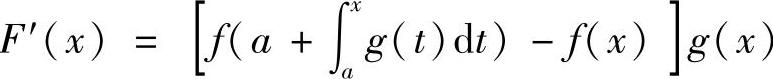
≤[f(a+(x-a))-f(x)]g(x)(利用f(x)在[a,b]上单调增加及(Ⅰ)的结论)
=0,
所以,F(b)≤F(a)=0,即
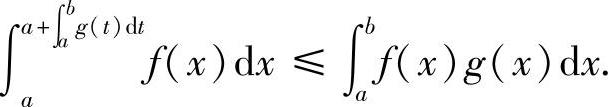
附注 由于已证明了(Ⅰ),所以在证(Ⅱ)时,以把b改为x比较适宜.如果将a改为x,也同样可证,但此时需先证明:
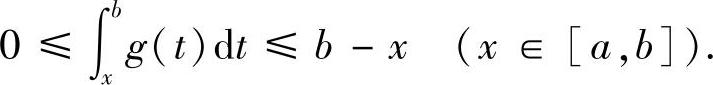
含积分不等式的证明方法在基础篇第二章九有详细的叙述,而且在这节中可以找到与本题类似的例题.
(20)分析 (Ⅰ)对矩阵A施行初等行变换化为阶梯形矩阵,求出方程组Ax=0的一个基础解系.
(Ⅱ)用解矩阵方法算出满足AB=E的所有矩阵B.
精解 (Ⅰ)由于
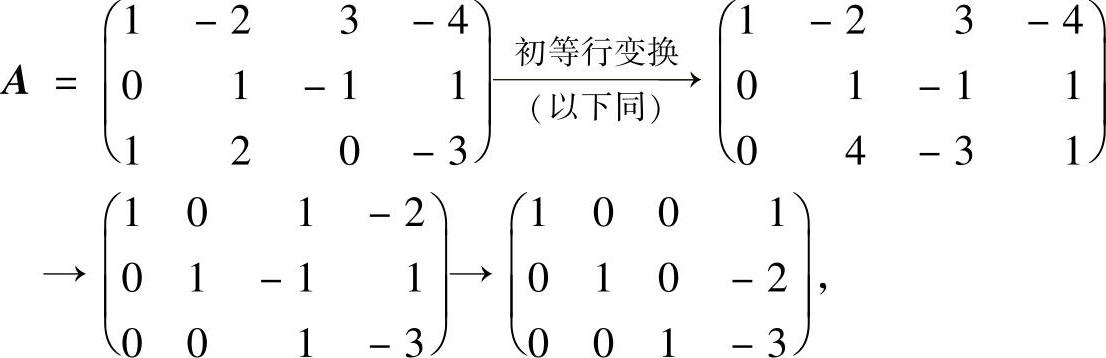
所以方程组Ax=0的一个基础解系为(-1,2,3,1)T.
(Ⅱ)记B=(β1,β2,β3)(其中β1,β2,β3都是4维列向量),则AB=E
即为三个方程组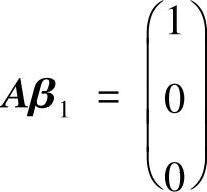 ,
,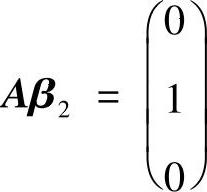 ,A
,A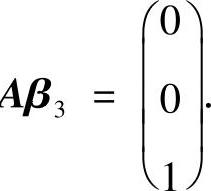
由于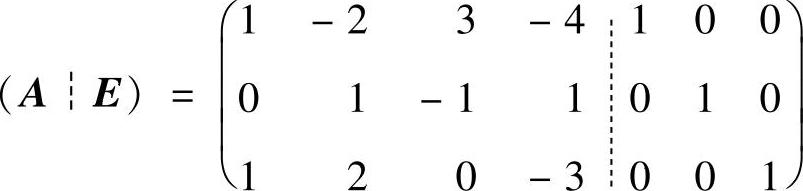

所以,Aβ1=0的基础解系为(-1,2,3,1)T,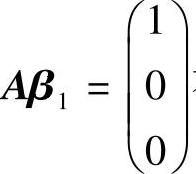 有特解(2,-1,-1,0)T.
有特解(2,-1,-1,0)T.
从而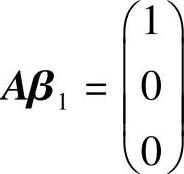 的通解为
的通解为
β1=c1(-1,2,3,1)T+(2,-1,-1,0)T=(-c1+2,2c1-1,3c1-1,c1)T.
同样可得
β2=(-c2+6,2c2-3,3c2-4,c2)T,
β3=(-c3-1,2c3+1,3c3+1,c3)T.
因此,满足AB=E的所有矩阵B为
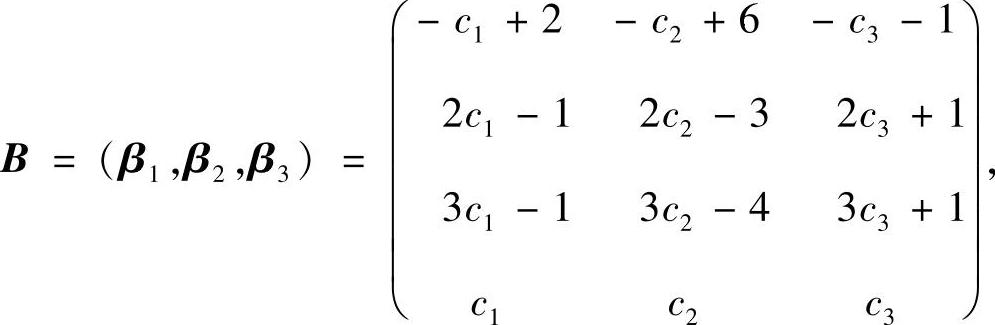
其中c1,c2,c3是任意常数.
附注 本题(Ⅱ)是矩阵方程的求解.
矩阵方程 AX=B (∗)
的解法如下:
当A可逆时,X=A-1B.
当A不可逆时,对式(∗)的增广矩阵(A┆B)施行初等行变换,成为(C┆D)(其中C是阶梯形矩阵,要求每个非零行的最左边元素都为1).由此可以算出Ax=0的一个基础解系ξ1,ξ2,…,ξr,记γ=c1ξ1+c2ξ2+…+crξr(其中,c1,c2,…,cr是任意常数),也可以算出各个方程组Ax=β1,Ax=β2,…,Ax=βl(其中β1,β2,…,βl是B的所有列向量)的特解γ1,γ2,…,γl,则
X=(γ+γ1,γ+γ2,…,γ+γl).
矩阵方程的解在基础篇第六章三中作了详细叙述,在这一节及提高篇18中可以找到与本题十分相似的例题.
(21)分析 只要证明矩阵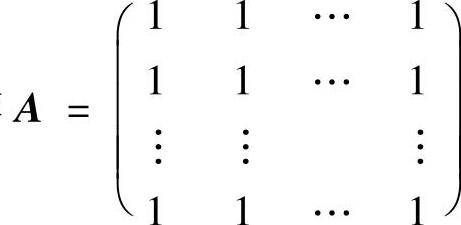 和矩阵
和矩阵 都可相似对角化,且它们具有相同的对角形矩阵即可.
都可相似对角化,且它们具有相同的对角形矩阵即可.
精解 记E是n阶单位矩阵,则由
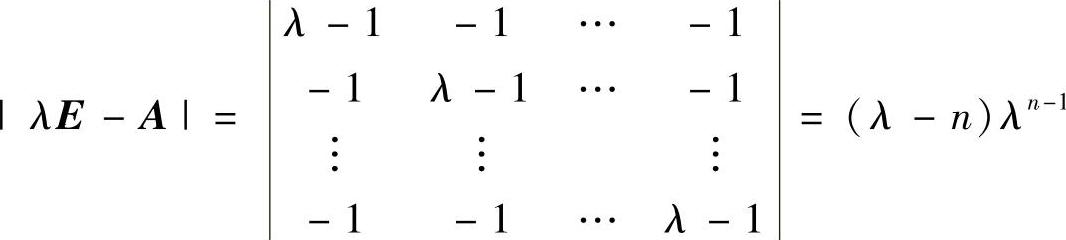
知,A有特征值λ=n,0(n-1重).由于A是实对称矩阵,所以A可相似对角化,且
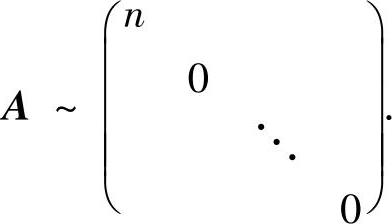
由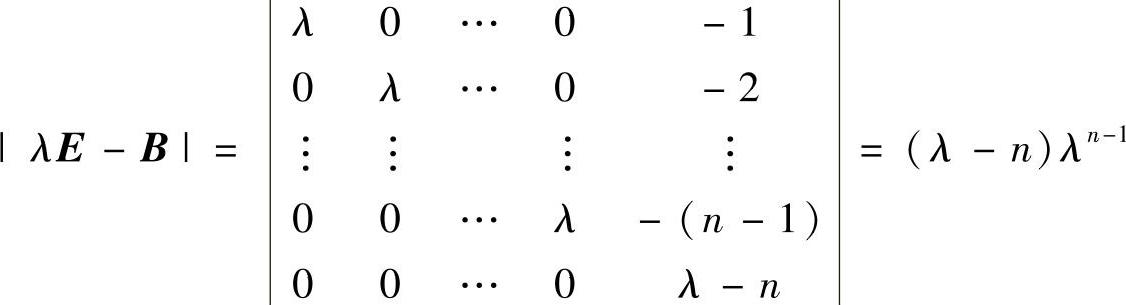 知,B有特征值λ=n,0(n-1重).
知,B有特征值λ=n,0(n-1重).
设B的对应λ=n的特征向量为α=(a1,a2,…,an)T,则
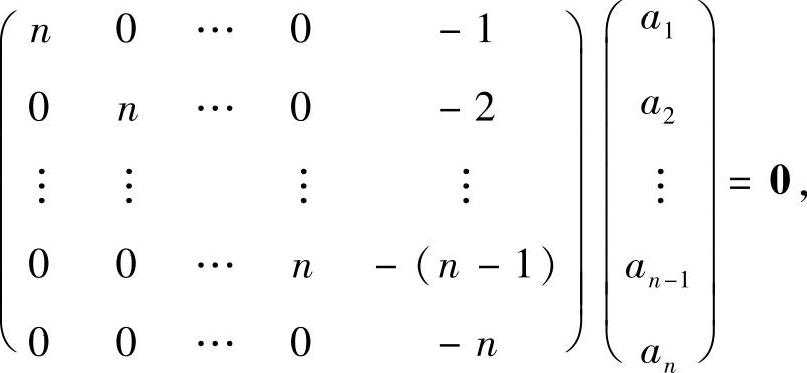
故可取α=η1=(1,2,…,n)T.
设B的对应λ=0的特征向量为β=(b1,b2,…,bn)T,则
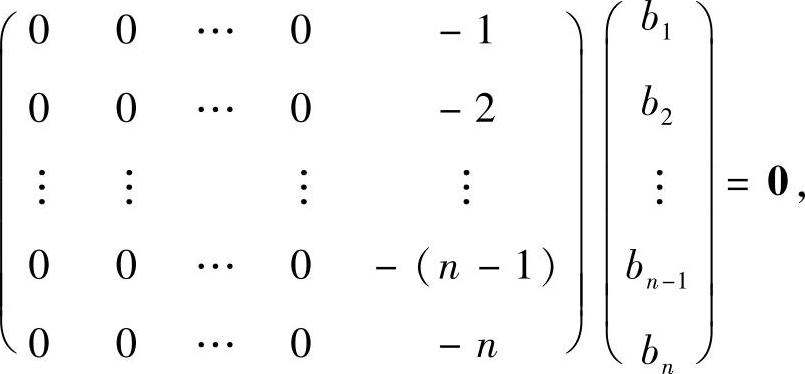
显然bn=0,b1,b2,…,bn-1可以任取,故取β为
η2=(1,0,0,…,0,0)T,
η3=(0,1,0,…,0,0)T,
︙
ηn=(0,0,0,…,1,0)T,
于是,B有n个线性无关的特征向量η1,η2,…,ηn,所以B可相似对角化,且
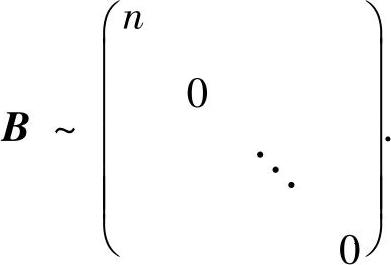
因此A与B相似.
附注 应当注意:当两个n阶矩阵A与B有相同的特征值时,它们未必相似;但是当A与B有相同的特征值,且都有n个线性无关的特征向量时,它们必相似.
本题实际上是n阶矩阵相似对角化的问题,在基础篇中详细总结了n阶矩阵可相似对角化的条件及相似对角化的方法.
(22)分析 (Ⅰ)先写出在(0,a)上服从均匀分布的随机变量U的分布函数,然后按分布函数的定义计算Y的分布函数FY(y).
(Ⅱ)利用(Ⅰ)算出Y的概率密度fY(y),然后按数学期望计算公式计算EY.
精解 (Ⅰ)设U~U(0,a),则U的分布函数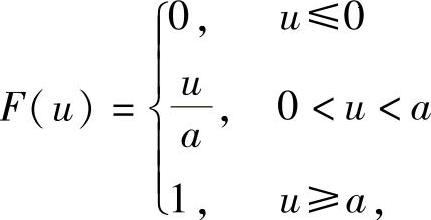 ,所以Y的分布函数为
,所以Y的分布函数为
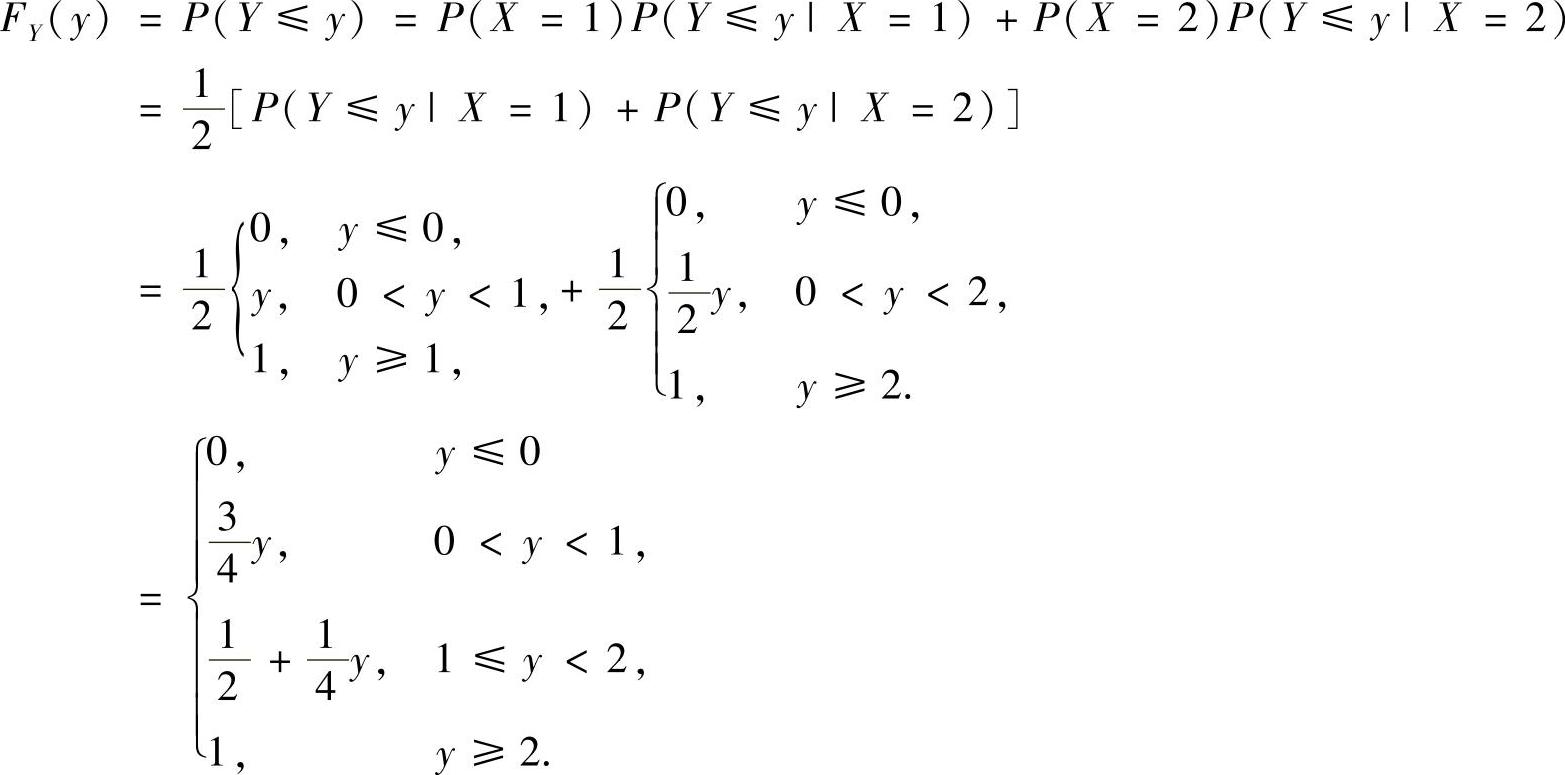
(Ⅱ)由(Ⅰ)可知,Y的概率密度 所以
所以
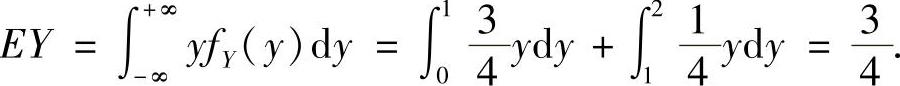
附注 顺便计算DY:
由于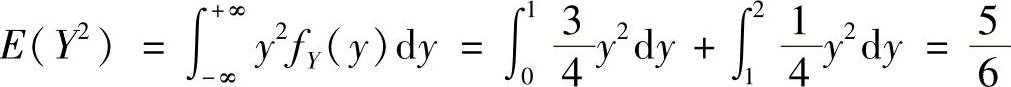 ,所以
,所以
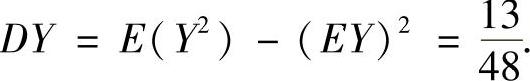
本题的关于Y的分布函数FY(y)的计算可以从提高篇21中找到类似的例子.
(23)分析 (Ⅰ)利用X,Y的概率分布与(X,Y)的概率分布的关系计算(X,Y)的概率分布.
(Ⅱ)利用(Ⅰ)中算出的(X,Y)分布计算概率P(X+Y≤1).
精解 记p=P(X=1,Y=1),则
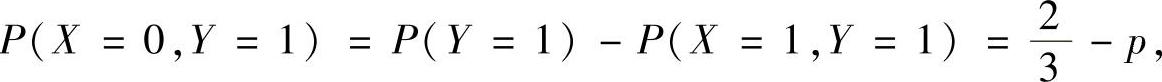
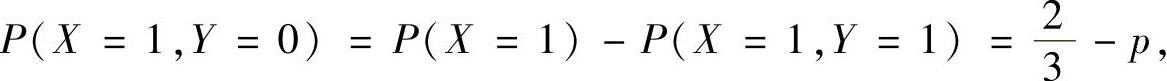
所以,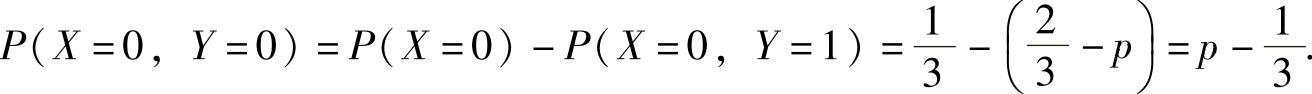
由此得到(X,Y)的概率分布为
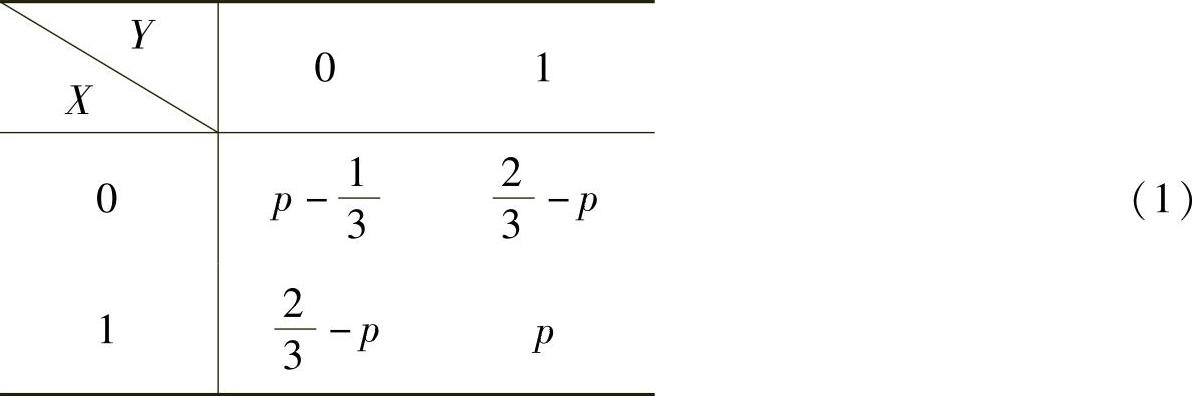
容易知道E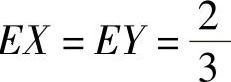 ,
,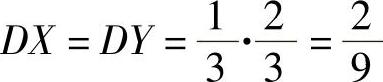 ,以及由式(1)知
,以及由式(1)知
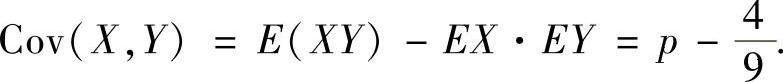
所以由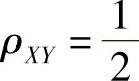 ,即
,即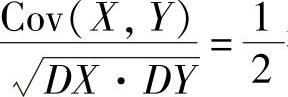 得
得
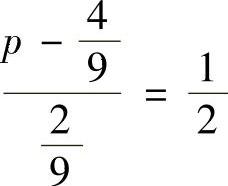 ,即
,即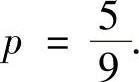
将它代入式(1)得(X,Y)的分布为
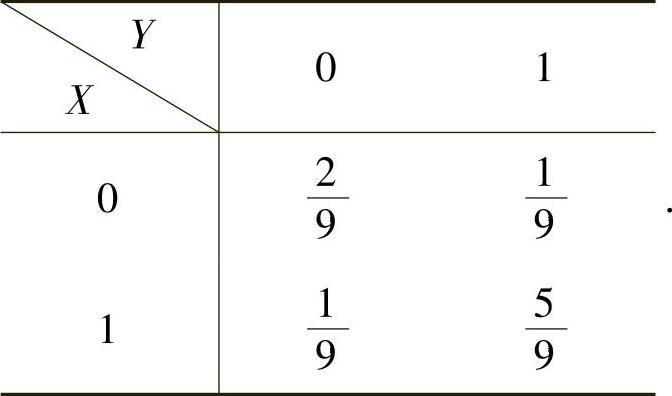
(Ⅱ)由(Ⅰ)得
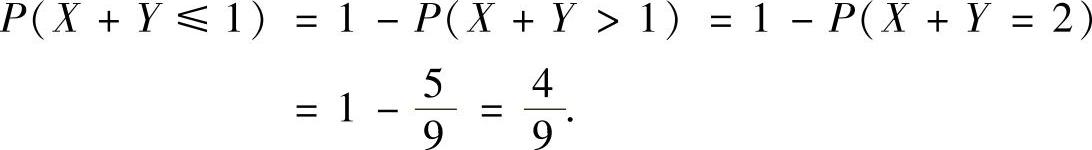
附注 题解中有两点值得注意:
(Ⅰ)设p=P(X=1,Y=1),使计算简单些.
(Ⅱ)要记住服从0-1分布的随机变量U的EU=p,DU=p(1-p),其中p=P(U=1).
本题的关于(X,Y)的概率分布计算可以从提高篇21中找到类似的例题.
