假言推理及其逻辑特征
假言推理是指前提中至少有一个是假言命题,并根据假言命题前、后件逻辑关系而进行推演的演绎推理。在假言推理中,根据假言前提是充分条件、必要条件和充要条件可以把假言推理分为充分条件假言推理、必要条件假言推理和充要条件假言推理几种。
(一)充分条件假言推理
前提由一个充分条件假言命题一个性质命题构成,推理依据充分条件假言命题的逻辑特征进行。充分条件假言命题的逻辑特征是:“前件p存在,后件q必然存在;后件q不存在,前件p就不存在。”因此,充分条件假言推理有两种正确推理形式。
1.肯定前件式
性质命题肯定假言命题的前件,结论肯定假言命题的后件。推理形式如下:
如果p,那么q
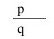
(式中p表示为前件,q表示为后件。)
例如:
如果罪犯目的是盗窃,那就会拿走被害人的财物和现金;
罪犯拿走了保险柜里的现金和一些贵重物品;
罪犯目的是盗窃
2.否定后件式
性质命题否定假言命题的后件,结论否定假言命题的前件。推理形式如下:
如果p,那么q
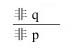
例如:
如果罪犯目的是盗窃,那就会拿走被害人的财物和现金;
罪犯没有拿走了保险柜里的现金和贵重物品;
罪犯目的不是盗窃
(二)必要条件假言推理(https://www.daowen.com)
必要条件假言命题是根据必要条件假言命题的逻辑特征进行推演的。必要条件假言命题的逻辑特征是:前件P不存在,后件q就必然不存在,后件q存在,前件P就必然存在。因此,必要条件假言推理有两种正确推理形式:
1.否定前件式
只有p,才q
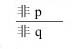
例如:
只有与被害人熟悉的人才是作案人;
甲与被害人不熟悉;
甲不是作案人
2.肯定后件式
只有q,才p
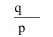
例如:
只有与被害人熟悉的人才能把门叫开而将被害人杀害;
现查,把门叫开而杀害被害人的是甲;
甲与被害人熟悉
(三)假言连锁推理
假言连锁推理亦称纯假言三段论推理。前提和结论都为假言命题的假言推理。这种推理是通过前提中第一个假言前提的后件与后一个假言前提的前件相同而将两个假言前提联结起来,从而推出一个假言命题的结论。这种假言命题至少是两个假言前提构成也可以是两个以上的假言前提构成。推理结构如下:
如果p,那么q;
如果q,那么r;
如果p,那么r
例如:
如果水中有高浓度的酸性物质,那么水就有防腐的作用;
如果水有防腐的作用,那么浸泡在水中的尸体就不易腐烂;
现查水中确实有高浓度的酸性物质,浸泡在水中的尸体不易腐烂[1]
这就是一个纯假言推理。显然,纯假言推理也可以从否定后件到否定前件。
