一、多值逻辑概述
多值逻辑(many-valued logic)是一种非古典逻辑,是讨论命题具有“真”、“假”值和其他值的逻辑。所谓其他值是指除“真”和“假”以外的,具有三个或三个以上的多值。所谓多值逻辑是相对于二值逻辑而言的,我们平常所谓二值逻辑是指一个命题的逻辑值要么真要么假,没有介乎于两者之间的第三种情况存在,逻辑上把这叫做“二价法则”,这种“二价法则”与逻辑基本规律矛盾律和排中律紧密联系,普通逻辑的系统就是建立在二值逻辑的基础之上的。而多值逻辑则是研究一个命题具有三个或者三个以上值的命题之间的逻辑关系,它是现代逻辑发展的产物(本书只对多值判断的逻辑特征进行初步介绍)。
多值逻辑的发展渊源可以追溯到亚里士多德,他认为将来可能事件的命题实际上是既不真又不假,真假都是可能的,在事件发生之前至少有三个未定的值。这与传统逻辑的“二价法则”是不相容的。最早的多值逻辑系统是由波兰逻辑学家卢卡西维茨和波斯特于20世纪20年代提出来的。卢卡西维茨在分析将来偶然命题时注意到仅用真假二值来表述是不充分的。比如,“明年12月21日这天中午我在华沙”这一陈述是可能但非必然真的,因为现在还不能对这句话的真假加以肯定或者否定,即现在陈述“明年12月21日中午我将在华沙”,是既不真又不假的。如果它真,那么它就是必然的;如果它假,则又是不可能的了,它应是“可能但非必然的”。单用真假二值无法对其进行表述,这种陈述应有第三种值,这种值不同于假(0)也不同于真(1),而是一种可能(1/2),这种可能与真假是平行的。赖辛巴赫从量子力学角度提供了支持卢卡西维茨的新证据。
我们都知道,在二值逻辑中,命题的真值情况如下:
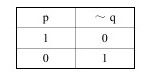
1.一个命题P真,它的否定命题~P则假;一个命题P为假,则它的否定命题~P为真。例如:
“犯罪嫌疑人是一个女性”为真,则“犯罪嫌疑人不是一个女性”为假;
“犯罪嫌疑人是一个女性”为假,则“犯罪嫌疑人不是一个女性”为真。
以下是各种复会命题的真值表:
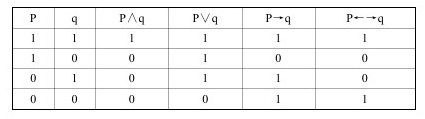
2.一个联言命题(P∧q)只要其中有一个支命题为假,则该命题为假。例如:
“甲和乙是盗窃犯”为假,
只要
“甲是盗窃犯”假,
或者是
“乙是盗窃犯”假。
3.一个选言命题(P∨q),只要其中一个支命题为真,该选言命题为真。例如:
“甲或者乙是犯罪嫌疑人”真,
只要
“甲是犯罪嫌疑人”真,或者“乙是犯罪嫌疑人”真。
4.一个蕴涵命题(P→q),只有当前件P真并且后件q假时,该蕴涵才为假。例如:
“如果甲没有作案时间,那么甲就不是作案人”假,
必然是
“甲没有作案时间”真,并且“甲不是作案人”假。
5.一个等值命题(P←→q),只有当前件P和后件q同真或者同假时,该命题为真。例如:
“当且仅当世界上出现了阶级,世界上才出现国家”真,
必然是
“世界上出现阶级”和“世界上出现国家”同真或者同假。
按照传统二值逻辑,下列公式都是永真式:
A.同一律(P→P)
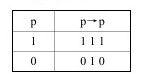
例如:
“如果甲是作案人,那么甲是作案人”为真。
B.排中律(P∨~P)
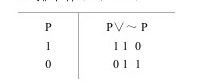
例如:
“甲是犯罪嫌疑人或甲不是犯罪嫌疑人”为真。
C.矛盾律(~(P∧~P)

例如:
“并非‘甲是作案人又不是作案人’”为真。
传统逻辑的三个规律,无论P取真或假值都为真。
下面,我们研究卢卡西维茨的三值逻辑。仍然是通过真值表来进行研究。
真值表如下:
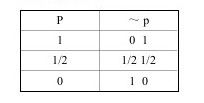
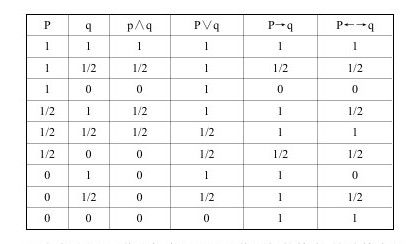
由上表可知,三值逻辑有不同于二值逻辑的特点,这些特点是:
第一,一个命题P取可能值(1/2),其否定命题~P也取可能值(1/2)。如:
“甲是犯罪嫌疑人”是可能的,“甲不是犯罪嫌疑人”也是可能的。
第二,对于一个联言命题(P∧q),其中只要有一个支命题(P、q)逻辑值断定最小,该命题就取这个最小的值。从(P、q)的真值来看,显然1>1/2>0。真值表中,涉及可能的情况有5种,它们的真值如下:
甲是杀人犯(p)并且是强奸犯(q)
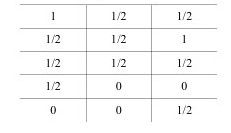
第三,对于一个选言命题(P∨q)而言,其中哪个肢命题(P、q)的逻辑值最大,该选言命题就取这个值。选言命题涉及1/2这种真值的情况有5种,它们的真值如下:
或者甲是杀人犯(p)或者乙是杀人犯(q)
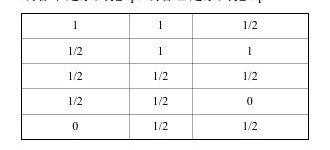
第四,对于一个蕴涵命题(P→q)而言,只有在其前件P真而后件q假时,该蕴涵命题为假,蕴涵命题为假和传统逻辑是相同的。不过,当蕴涵的前件或者后件出现可能(1/2)时,该蕴涵却出现以下情况:
如果甲是杀人犯(P),那么甲具有作案时间(q)
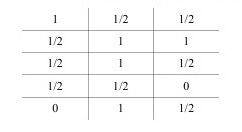
真值表说明,出现可能性蕴涵命题的情况只有两种情况:前件真而后件可能,前件可能后件假。
第五,对于一个等值命题(P←→q)而言,当前件和后件同值时,该命题取真值。所谓同值,除了同真、同假之外,也包括可能(1/2)。当命题的前件或者后件仅仅出现了一种可能(1/2)时,该命题取可能值(1/2)。
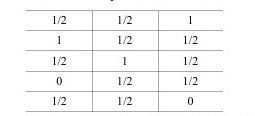
乙是杀人犯(q),当且仅当甲是杀人犯(P)
前面我们曾提到,二值逻辑中的基本规律是同一律和不矛盾律和排中律,但是在三值逻辑中,不矛盾律和排中律已经不是基本规律了,不矛盾律的真值表如下:
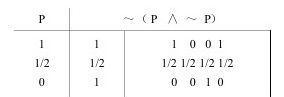
排中律的真值表如下:
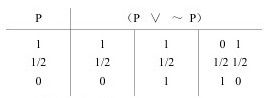
同一律的真值表如下
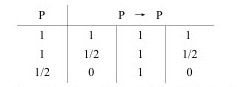
这说明,同一律在三值逻辑中是一个永真式。
多值逻辑不仅仅局限于三值,而且可以运用于无限值的系统,这些值可以用0—1之间的实数来表达。以下是对命题具有多值情况的直观描述:
a.“罪犯是一个男性(P)”,此命题为二值时为:0,1
b.“罪犯是一个男性(P)”,此命题为三值时为:0,1/2,1
c.“罪犯是一个男性(P)”,此命题为四值时为:0,1/3,2/3,1
d.“罪犯是一个男性(P)”,此命题为五值时为:0,1/4,2/4,3/4,1
e.“罪犯是一个男性(P)”,此命题为六值时为:0,1/5,2/5,3/5,4/5,1
……
由此观之,多值逻辑的规律是:
第一,多值逻辑的最大值是1,最小值是0,介于0—1之间的值是分数。
第二,介于0—1之间的分数之分母是由值的个数减去1,分子的最大数是由分母减去1。假定n为任意的值(n≥2),具有n值的命题就有如下的真值:
0,1/n1,2/n1,3/n1,4/n1……n2/n1,1
假定n=10,10个值就是:
0,1/9,2/9,3/9,4/9,5/9,6/9,7/9,8/9,1
在多值逻辑中,我们用“/P/”表示P是多值系统中的命题,这种表示方法与二值逻辑的表示区别开来。下面,我们在三值逻辑基础上进一步研究复合命题在多值情况下的真值表。
1./~P/
在三值逻辑中,~P的真值表是:
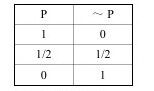
该真值表说明:
当P=1时,~P=11=0
当P=1/2时,~P=11/2=1/2
当P=0时,~P=10=1
当我们将它推广到更多值的情况时,即:
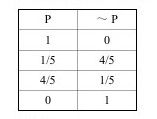
……
真值表告诉我们:/~P/=1/P/
这说明,当一个命题P为真的值越大时,~P为假的值就小;反之,当一个命题为假的值越小时,~P为真的值就越大。例如:
“犯罪嫌疑人甲作案的可能性极小(约有30%的可能性)”
“犯罪嫌疑人甲不作案的可能性极大(约有70%的可能性)”
2./P∧q/
前面我们曾讨论过联言命题在三值逻辑中的真值情况,一个联言命题的真值取决于命题中支命题的最小值,因此:
/P∧q/=/P/、/q/值的比较,最小值则是该命题的逻辑值。当
/P/=1,/q/=0时,/P∧q/=0;
/p/=1/5,/q/=2/5时,/P∧q/=1/5;
/P/=2/10,/q/=2/10时,/P∧q/=2/10;
/P/=0,/q/=9/10时,/P∧q/=0;
……
例如:
“甲和乙都是犯罪嫌疑人”中,当“甲是犯罪嫌疑人(P)”为90%的可能,“乙是犯罪嫌疑人(q)”为50%的可能时,“甲和乙是犯罪嫌疑人”这个联言判断是50%的可能。
又如:
“甲和乙都是犯罪嫌疑人”中,当“甲是犯罪嫌疑人(P)”为假(0),“乙是犯罪嫌疑人(q)”为90%的可能时,联言判断“甲和乙是犯罪嫌疑人”为假(0)。
3./P∨q/
在三值逻辑中,选言命题的值取决于支命题的最大值。因此:
当/P/=1,/q/=4/5时,/P∨q/=1;
当/P/=0,/q/=9/10时,/P∨q/=9/10;
当/P/=0,/q/=0时,/P∨q/=0;
当/P/=2/5,/q/=2/5时,/P∨q/=2/5;
……
例如:
“或者甲是犯罪嫌疑人或者乙是犯罪嫌疑人”中,当“甲是犯罪嫌疑人”为真(1),“乙是犯罪嫌疑人”为50%可能时,“或者甲是犯罪嫌疑人或者乙是犯罪嫌疑人”为真(1)。
“甲是犯罪嫌疑人”为假(0);“乙是犯罪嫌疑人”为20%可能时,“或者甲是犯罪嫌疑人或者乙是犯罪嫌疑人”这个选言判断为20%的可能。
“甲是犯罪嫌疑人”为50%可能;“乙是犯罪嫌疑人”为50%可能时,“或者甲是犯罪嫌疑人或者乙是犯罪嫌疑人”这个选言判断为50%的可能。
4./P→q/
在三值逻辑中,蕴涵命题的真值情况是:
当P=q时,(P→q)=1
当P<q时,(P→q)=1
当P>q时,(P→q)=1 P+q
例如:
当/P/=40%,/q/=40%时,/P→q/=1
当/P/=70%,/q/=80%时,/P→q/=1
当/P/=70%,/q/=50%时,/P→q/=1 70%+50%=80%
……
例如:
“如果甲是犯罪嫌疑人(P),那么乙就是犯罪嫌疑人(q)”这一假言判断,当前件P为50%可能,后件q也为50%的可能时,该蕴涵命题为真;
当“甲是犯罪嫌疑人(P)”为50%可能,“乙是犯罪嫌疑人(q)”为80%可能时,该蕴涵命题为真;
当“甲是犯罪嫌疑人(P)”为50%,“乙是犯罪嫌疑人(q)”为30%时,该蕴涵命题的值等于1~50%+30%,即80%。
5./P←→q/
在三值逻辑中,等值命题的取值情况是:
当P=q时,(P←→q)=1
当P>q时,(P←→q)=1 P+q
当P<q时,(P←→q)=1 q+P
因此:
当/P/=/q/时,/P←→q/=1
当/P/>/q/时,/P←→q/=1/p/+/q/
当/P/</q/时,/P←→q/=1/q/+/p/
例如:
“甲是作案人(q),当且仅当甲具有作案时间(p)”。当甲具有作案时间为50%可能,甲是作案人有50%可能时,该命题是真的;
当甲具有作案时间(p)为50%可能,甲是作案人(q)有40%可能时,该命题的真值=1/P/+/q/,即90%;
当甲具有作案时间(p)为40%可能,甲是作案人(q)为50%可能时,该命题的真值=1/q/+/P/,即90%[1]。
