结果分析与讨论
基于以上基础数据和模型参数，并设决策者愿意用3%的物流成本的升高换取物流网络整体碳排放成本的降低，目标函数一的松弛系数ε＝3%，我们用Cplex软件双目标数学规划模型进行求解，可得模型满意解如表5－4至图5－6所示。
表5－4 候选无水港布局选择结果
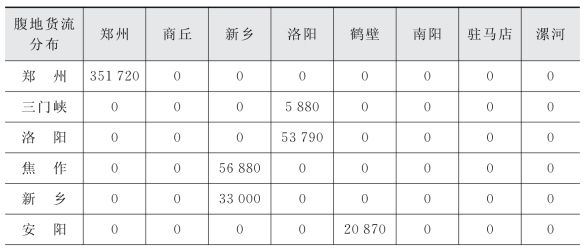
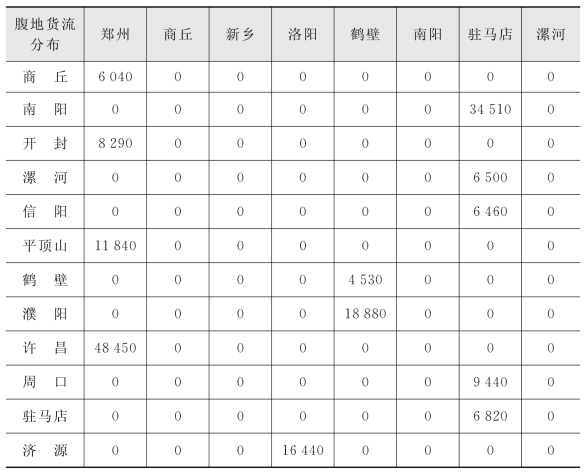
表5－5 腹地到无水港的货流配置情况
续表
表5－6 无水港到海港的货流配置情况
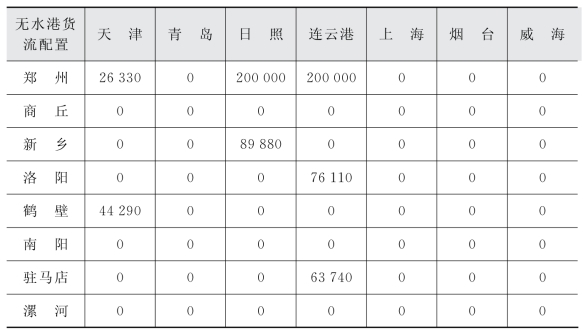
表5－4是候选无水港的选择布局结果，表中“1”表示对应的候选无水港被物流网络方案满意解选中作为布局节点，“0”表示未被选中。可以看到，8个候选无水港的5个被选中为要布局的无水港，其候选无水港城市分别为郑州、新乡、洛阳、鹤壁和驻马店。
表5－5既显示了18个腹地节点与无水港节点的邻接关系，即腹地节点到无水港节点有货流配置的节点对之间就存在邻接关系，同时货流配置数量则表示了对应无水港对腹地节点的物流服务量。例如，表5－5中的“6 040”数据就表示了商丘节点由郑州无水港节点提供物流服务，且物流服务流量为6 040TEU，然后通过郑州无水港连接到某海港，实现商丘外贸货物向海外市场的出口。
表5－6表示了无水港与海港之间的合作关系，以及无水港到海港的货流配置情况。如果无水港—海港节点对对应数据是“0”，则它们之间不存在直接邻接合作关系，如果不是“0”，说明它们之间存在邻接合作关系，且对应数据值就是该无水港向该海港配置的货流流量。
考虑到7个海港、8个候选无水港之间的成本折扣，以及18个腹地节点、8个候选无水港节点、7个海港节点构成的物流网络的货运碳排放约束，在决策者用3%的物流成本升高换取碳减排效益的决策意愿下的腹地—无水港—海港物流网络布局全貌。在该满意解下，网络整体物流成本为－Y9.467 966×109，碳排放量为3.113 8×108吨。
以上所有结果由决策者愿意用3%的物流总成本松弛来换取碳减排环境效益的前提条件，以及海港对无水港成本折扣合作关系评价基础上获得的。本书接下来将要讨论分析海港对无水港的成本折让合作关系、决策者物流成本松弛意愿等因素对无水港—海港物流网络location－allocation设计的影响。