结果分析与讨论
依据上述网络参数设置和遗传算法参数设置，得Pareto最优解分布如图6－2所示。
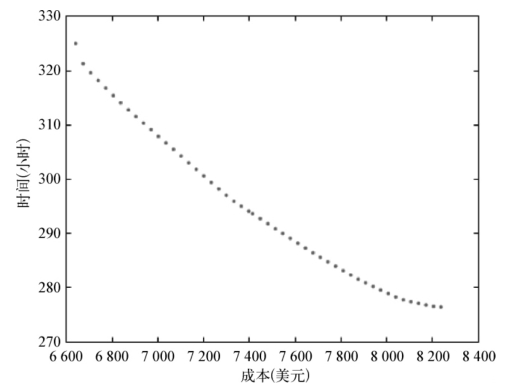
图6－2 案例网络货流配置双目标数目规划Pareto最优解分布
应用双目标遗传算法求解，共得到了50个Pareto最优解。图6－2给出了全部的最优成本与时间目标解组合，可以获得在不同的成本目标值下运输所需的最小时间目标值，为物流集成商综合考虑货物属性及客户成本、时间需求下，通过设置不同的成本目标和时间目标侧重程度，实现最优方案的选择提供了参考。
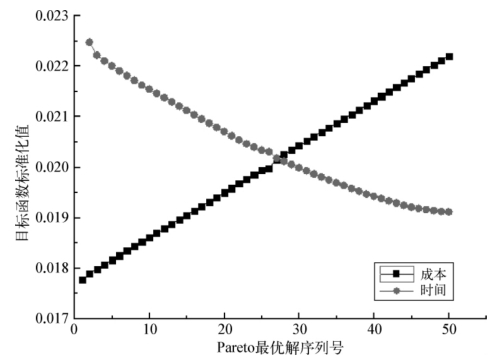
对这50个Pareto最优解的目标函数值进行［0～1］的标准化处理，绘制出不同Pareto最优解中成本和时间的变化趋势图，见图6－3。
根据图6－2和图6－3可以看出，跨境物流网络中的内陆货物运输时间和运输成本呈相反的变化趋势。由图6－3中标准化后的运输时间变化曲线可以看出，从Pareto最优解序号30开始，当成本仍均匀上升的时候，时间的降低速率在减小，这就说明用相同程度的成本提升换来时间效率的提高的效用降低了，即与前30个Pareto最优解相比，想要获得相同时间的降低，则需要更高的运输成本升高为代价。因此，本书对Pareto最优解排序30的最优方案进行了专门分析。该最优解的最小成本为7 579.093美元，最小时间为289.080 2小时，而只考虑最小成本单目标情况下的最小成本为6 590.528美元，此时的运输时间为325.054 3小时，该最优方案相当于比只考虑成本目标时的成本值提升了15%，而运输时间节省了36个小时，将其称之为最小成本松弛15%情况下的最优解。
图6－3 50个Pareto最优解的成本和时间目标函数值变化趋势
由图6－2还可以看出，当只考虑最小时间单目标时，最小成本为8 238.143美元，比只考虑最小成本单目标下的最小成本目标函数值提升了25%的比例，也就是说，集成商可以用25%的成本增长换取运输的最短时间。还可以说明，集成商通过调节运输成本换取运输时间的松弛空间为［0～25%］。
对只考虑最小成本，只考虑最小时间，以及前面提到了的成本提升15%情况下的最优解对应的货流配置方案进行统计，结果如表6－4所示。
表6－4 最优解对应的网络货物流配置方案
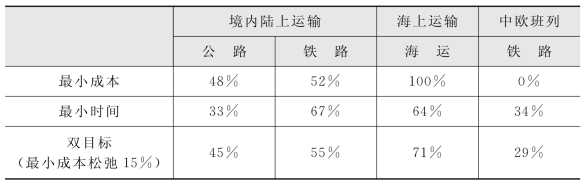
通过表6－4可以得到如下结论：