资金时间价值的基本计算公式
一、资金的等值原理
（一）资金等值的含义
“等值”是指在时间因素的作用下，在不同的时间点绝对值不等的资金具有相同的价值。例如当年利率为6%时，则现在的100元与1年后的106元虽然绝对数量不等，但是这两个时间点上的两笔资金是“等值”的。
由于资金存在时间价值，这样在不同时间点上发生的现金流量其数值不能直接相加减，为了达到对投资项目的现金流量进行计算和分析的目的，需将一个或一系列时间点发生的资金转换成另一个或一系列时间点的等值的资金额，然后再来进行计算和分析，这样的一个转换过程就称为资金的等值计算。
影响资金等值的因素很多，主要有金额的大小、金额发生的时间、利率的大小。其中利率是一个关键因素，一般等值计算中是以同一利率为依据的。
（二）资金等值计算的有关概念
（1）现值P。又称初值，是指发生在时间序列起点处的资金值。
（2）终值F。即资金发生在（或折算为）某一特定时间序列终点的价值。
（3）时值与时点。资金的数值由于计算利息和随着时间的延长而增值，在每个计息期期末的数值是不同的，在某个资金时间节点上的数值称为时值。现金流量图上，时间轴上的某一点称为时点。
（4）年金A。指各年等额收入或支付的金额，通常以等额序列表示，即在某一特定时间序列期内，每个相同时间收支的等额款项。
（5）折现。将时点处资金的时值折算为现值的过程称为折现，即等值过程。在资金时间价值计算中，等值是一个十分重要的概念，资金时间价值计算的核心就是进行等值计算。
（6）利率i。指在一定时间段内产生的利息或利润与原来的本金或资金额的比率，也称为使用资金的报酬率。在不同的状况下，其名称也不相同，也称为贴现率或基准收益率。
二、资金的等值计算
根据支付方式和等值换算点的不同，资金等值计算公式可分为一次支付类型、等额支付类型和变额支付类型。本章主要介绍一次支付类型、等额支付类型以及变额支付中的等差多次支付类型。
（一）一次支付利息的情形
一次支付又称整付，是指所分析系统的现金流量，无论是流入或是流出，均在一个时点上一次发生，其现金流量图如图3-4所示。
图3-4 现金流量图
1．一次支付终值公式（已知P，求F）
在某一时点上，有资金P，计息期利率为i，计算按复利得到的第n期末的本金和。其现金流量图如图3-5所示。根据式（3-4）得一次支付终值公式：
图3-5 一次支付终值现金流量图
Fn=P（1+i）n
上式可以表示为
其中，（1+i）n或（F/P，i，n）称为一次支付终值系数或因子。公式中的系数或因子（F/P，i，n）可以从复利系数表（见附表1）中查得。
【例3-4】某人现在将50000元存入银行，银行存款年利率为5%，则他3年后取出钱的本金和为多少？
解：由式（3-4），得
F=P（1+i）n=50000×（1+5%）3=57881．25（元）
即，50000元在年利率为5%时，经过3年以后本金和为57881．25元，增值7881．25元。
也可由式（3-7）计算，需查得系数（F/P，5%，3）。
2．一次支付现值公式（已知F，求P）
计划n年后累积资金为F，计息期利率为i，问现在需要一次投资P值。也就是将未来的某一时点的资金价值换算成资金的现值。其现金流量图如图3-6所示。
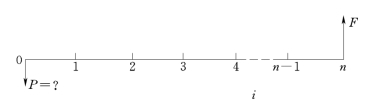
图3-6 一次支付现值现金流量图
根据式（3-4）得一次支付现值公式：
式（3-8）可以表示为
其中，
或（P/F，i，n）称为一次支付现值系数或因子。公式中的系数或因子（P/F，i，n）可以在复利系数表（见附表2）中查得。
【例3-5】某投资项目计划在5年后得到1000万元的效益，收益率为10%，则现在需要投资多少？
解：根据式（3-8），得
即，现在应投资620．92万元。
（二）等额多次支付利息的情形
多次支付是指现金流量在多个时点发生，而不是集中在某一个时点上。如果现金流量是按相同的时间间隔发生的，各期利率均相等，而且各期发生的数额相等，这种情形称为等额多次支付情形。
1．等额多次支付终值公式（已知A，求F）
若每期期末支付一笔等额资金A，在利率为i时，计算n年后可一共支取的资金数额F。这类似于我们平常储蓄中的零存整取。其现金流量图如图3-7所示。
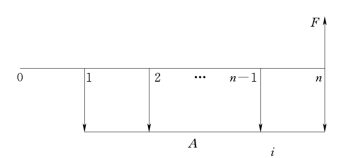
图3-7 等额多次支付终值流量图
根据一次支付终值公式可得等额多次支付终值公式：
上式可以表示为
其中，
或（F/A，i，n）称为等额多次支付终值系数或因子。公式中的系数或因子（F/A，i，n）可以从复利系数表（见附表3）中查得。
【例3-6】某人每年年末存入银行2000元，年利率为8%，则4年后可从银行取出多少钱？
解：根据式（3-10），得
即，4年后可从银行取出9012．22元。
2．等额多次支付现值公式（已知A，求P）
想要在以后的n期内每期末都能等额支取一笔资金A，计息期利率为i，计算现在应存入的资金数额P。其现金流量图如图3-8所示。
等额多次支付现值公式为
上式可以表示为
其中，
或（P/A，i，n）称为等额多次支付现值系数或年金系数。公式中的系数（P/A，i，n）可以从复利系数表（见附表5）中查得。
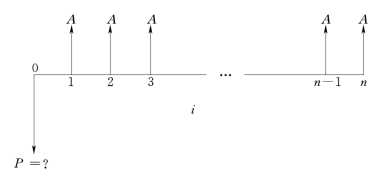
图3-8 等额多次支付现值流量图
【例3-7】为了在以后的10年中的每年年末都能取1000元，在年利率为6%的条件下，则现在需要向银行存入现金多少？
解：根据式（3-13），得
P=A（P/A，i，n）=1000×（P/A，6%，10）=1000×7．3601=7360．1（元）即，现在需要向银行存入现金7360．1元。
3．偿债基金公式（已知F，求A）
若想要在n年后一次性取出资金F，在计息期利率为i的情况下，求每个计息期期末应等额存入的资金额。其现金流量图如图3-9所示。
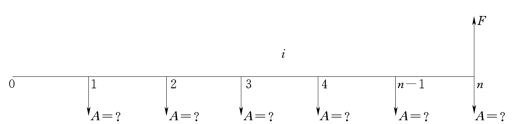
图3-9 偿债基金现金流量图
由式（3-10）可得偿债基金公式
上式可以表示为
其中，
或（A/F，i，n）称为偿债基金系数，它与等额多次支付终值系数互为倒数。公式中的系数（A/F，i，n）可以从复利系数表（见附表4）中查得。
【例3-8】某公司计划在第6年年末购置一处100万元的地皮，拟在这6年内的每年年末等额存入一笔资金到银行作为专用资金，银行存款年利率为10%，按复利计息，求每年等额存入的资金应为多少万元？
解：由式（3-15），得
A=F（A/F，i，n）=100×（A/F，10%，6）=100×0．1296=12．96（万元）
即，每年等额存入的资金应为12．96万元。
4．资金回收公式（已知P，求A）
若现在一次性投入资金数额为P，年利率为i，想要在此后的n年内全部收回，求每年年末应该等额回收的资金。其现金流量图如图3-10所示。
图3-10 资金回收现金流量图
由式（3-12），得资金回收公式为
上式可以表示为
其中，
或（A/P，i，n）称为资金回收系数。公式中的系数（A/P，i，n）可以从复利系数表（见附表6）中查得。
【例3-9】一台设备寿命周期为5年，购置时的成本为43295元，年利率为5%，求每年至少应获净收益多少可以收回投资。
解：由式（3-17），得
A=P（A/P，i，n）=43295×（A/P，5%，5）=43295×0．231≈10000（元）
即，每年至少应获净收益10000元才可以收回投资。
（三）等差多次支付利息的情形
在经济活动中，现金的收支常是不等额的，其中有一种比较典型的现金流动类型——等差序列现金流量。等差多次支付，即每期期末收支的现金流量序列是呈等差变化的。其现金流量图如图3-11所示。
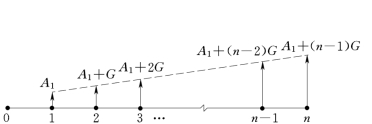
图3-11 等差多次支付现金流量图
由图3-11可分析知，等差系列可以分解为下列两个系列组成的现金流量图：一个是以A1为期末支付额的等额支付系列；另一个是由0，G，2G，…，（n-1）G组成的梯度系列。该梯度系列可以分解为（n-1）组期末支付为G的等额分付，其期数分别为n-1，n-2，…，2，1（见图3-12）。
图3-12 梯度系列的分解
1．等差支付现值公式（已知G，i，n，A1，求P）
下面是等差支付现值公式的推导过程：
第1期期末的现金流量的现值为P1=A1（1+i）-1；
第2期期末的现金流量的现值为P2=（A1+G）（1+i）-2；
第3期期末的现金流量的现值为P3=（A1+2G）（1+i）-3；
…
第n-1期期末的现金流量的现值为Pn-1=[A1+（n-2）G]（1+i）-（n-1）；
第n期期末的现金流量的现值为Pn=[A1+（n-1）G]（1+i）-n。
将第1期期末至第n期期末的现金流量现值相加，化简，得等差支付现值公式
上式可以表示为
其中，
或（P/G，i，n）称为等差多次支付现值系数。
2．等差多次支付终值公式（已知G，i，n，A1，求F）
等差多次支付终值公式为
上式可以表示为
其中，
或（F/G，i，n）称为等差多次支付终值系数。
3．等差序列年值公式（已知G，i，n，A1，求A）
根据现值和等额年金的关系，可得等差序列年值公式为
上式可以表示为
其中，
或（A/G，i，n）称为等差年金换算系数。公式中的系数（A/G，i，n）可以从复利系数表（见附表7）中查得。
【例3-10】某企业新购进一台设备，估计可用5年，不计残值。使用该设备第一年需支付维护费用5000元，以后逐年递增500元，年利率为10%，求设备维护费用的终值、现值。
解：由式（3-19）、式（3-20）、式（3-23），得
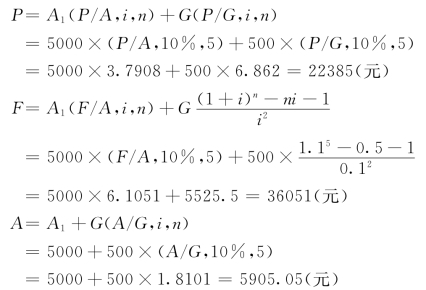
即，设备维护费用的现值为22385元，终值为36051元，等差年金为5905．05元。
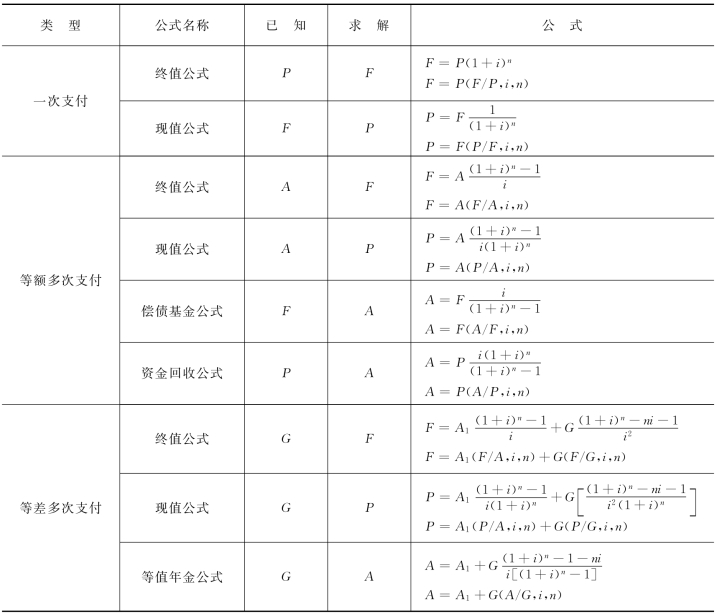
常用资金等值公式见表3-1。
表3-1 常用资金等值公式
