单指标排序综合法
一、方法简述
该方法从各个指标单独排序入手进行总的排序。设有n个评价指标，m个待评对象，首先根据单个评判指标分别对这m个对象进行单排序，数值相同的，序数取其平均值。然后求优先序频数矩阵R=（rij）mxn，表示被评对象Ai在n次指标单排序中，被派在第j位的加权频数。根据R阵，采用不同的准则，即可作为总排序。
对于各个不同的指标，统计学中经常结合数字的经济或社会意义，将指标划分为正指标和逆指标。正指标是指其经济和社会意义的大小和指标数值的大小成正比的指标，即所谓越大越好的指标；反之，若指标值大小与相应指标的经济和社会意义大小成反比的话，则称为逆指标，即所谓越小越好的指标。实际上这种划分应该在相对的意义上来理解才是正确的。
单指标排序综合法同一般的方法不一样，首先该方法是用指标的序数代替原来的指标值，这样就简化了数据，便于分析和处理。但这必然会带来信息损失，有可能破坏了原来数据的分布结构，使那些突出要素的贡献得不到充分的体现；其次，计算过程具有近似性，权数的本意是权衡轻重的，但在这里却转化成为频数，这种理解究竟合适不合适？只可以大致近似的认为它们是成立的；最后当某指标的数值出现重复时，采用将指标分解成几个子指标的方法加以解决，这样的做法思路清晰，易于理解，在不是很特殊的条件下还是很有价值的。
二、排序步骤
进行单排序，这里主要介绍两种做法的具体步骤。
（一）采用最大期望值法
从R矩阵的各列中选择出加权频数最大值，将此值视为最大期望值，据此排出总的次序，称为最大期望值法。当某列频数最大值不只一个时，则采用体育比赛中“算小分”的办法，即参考下一位次的频数值加以确定。
（二）采用线形规划方法
定义
则有
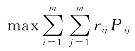
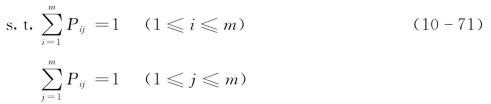
将rij视为Bi在总排序中的贡献，rij越大，分配Bi在总排序中处于第j位的可能性也就越大。这样，m个被评对象的总排序问题就变成了对每个位置（j=1，2，…，m）寻找方案，使得
取最大值的问题。这样就有m！个问题，当m很大时，等价于求解一个特殊的线性规划问题，又称为“线性分派问题”。
为了更好地对以上问题进行阐述，以下通过举例来说明此方法。
三、举例
对于某工程多指标综合评价的问题：从经济效益上对4个工程（B1、B2、B3、B4）进行评价，同时进行评判时采用6个评判指标（f1、f2、f3、f4、f5、f6），并且这6个指标所占的权重分别为W=（0．2、0．1、0．1、0．1、0．2、0．3），已知f4为逆指标，f1、f2、f3、f5、f6是正指标，见表10-17。
表10-17 工程资料数据表
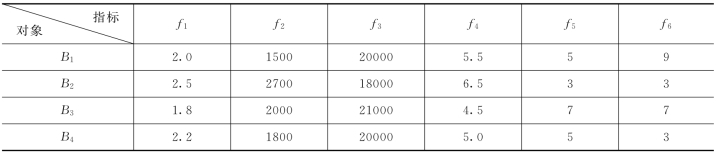
解：根据表10-17数据进行单排序，见表10-18。
从表10-18可以看出，第四列第三排是B1、B4，第六列第三排是B1、B4，表示数值相等，第七列第四排是B2、B4，排在同一个位置，因此应对此两项进行重新分析，见表10-19。
表10-18 排序表
表10-19 排序表
计算R矩阵，先计算其中的几个数，其他的各个数按照此计算方法进行计算（注意：如果是）：
设最优解为P*，由P*即可得出最优排序结果。经过分析可以知，与其相对应的线性分派问题的最优解为
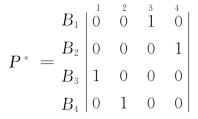
也即其最优排序为（B3、B4、B1、B2）。