层次分析法
层次分析法（AHP法）是一种以一个递阶层次结构模型求得每一个具体目标的权重，进而解决多目标决策的非数学模型优化方法，美国运筹学家T．L．Saaty于20世纪70年代中期提出。这种方法强调人的思维判断在决策过程中的作用，通过一定模式使决策思维过程规范化，体现了人们决策思维的基本特征：分解、判断、综合。它运用了定量与定性因素相结合，特别是定性因素起主导作用的决策问题，可用于处理复杂的社会、政治、经济等决策问题，是一种几乎不用高深数学工具和复杂运算的、简明有效的多目标决策方法。因此，自AHP法问世以来，在资源分配、管理和冲突分析中受到了人们、特别是决策者的欢迎并获得广泛应用，尤其被广泛地应用于确定指标的权重。
一、递阶层次结构的建立
递阶层次结构图如图10-8所示。
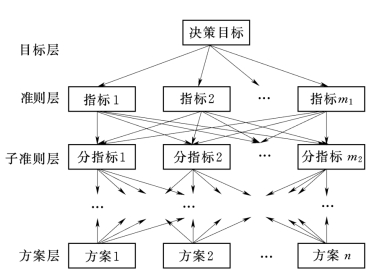
图10-8 递阶层次结构图
在研究复杂问题的时候，可以将复杂问题分解为各个元素，并可以将这些元素按不同的属性分成若干组，形成不同的层次。所有层次大体上分为目标层、准则层和方案层3类。处于最顶端的层次是目标层：决策目标。处于中间层次的是准则层，准则层包括各个指标，并且指标有层次之分，它是为了实现目标所涉及的环节，也即评价指标和分指标。处于最底层的是方案层，由为实现目标可供选择的各个方案、措施组成。
二、AHP法及其基本步骤
运用AHP法解决问题的基本过程分为建构AHP模型和求解AHP模型两大阶段。其中建构模型是核心问题和难点所在，求解模型阶段的比较、即两两判断比较子阶段的正确性则是决策正确的基础与前提。
首先要把系统分解成不同的组成因素，并按照各因素之间的相互关联，以及隶属关系分成不同层次的组合，构成一个多层次的分析结构模型，最终计算出最低层的诸因素相对于最高层相对重要性权值，从而确定出系统的综合得分，其基本步骤如下：
（1）建立层次结构模型。在深入分析实际问题的基础上，将有关的各个因素按照不同属性自上而下地分解成若干层次，同一层的诸因素从属于上一层的因素或对上层因素有影响，同时又支配下一层的因素或受到下层因素的作用。最上层为目标层，通常只有1个因素，最下层通常为方案或对象层，中间可以有一个或几个层次，通常为准则或指标层。当准则过多时，譬如多于9个时，应进一步分解出子准则层。
（2）构造成对比较阵。从层次结构模型的第2层开始，对于从属于（或影响）上一层每个因素的同一层诸因素，用成对比较法和1～9比较尺度构建成对比较阵，直到最下层。
（3）计算权向量，并作一致性检验。对于每一个成对比较阵计算最大特征根及对应特征向量，利用一致性指标、随机一致性指标和一致性比率作一致性检验。若检验通过，特征向量（归一化后）即为权向量；若不通过，需重新构建成对比较阵。
（4）计算组合权向量，并作组合一致性检验。计算最下层对目标的组合权向量，并根据公式作组合一致性检验。若检验通过，则可按照组合权向量表示的结果进行决策，否则需要重新考虑模型或重新构造那些一致性比率较大的成对比较阵。
三、构造两两比较的判断矩阵
建立了层次之后，上下层之间元素的相互关系就确定了。假设上一层次的某一元素Ci（i=1，2，3，…，m）对下一层次的元素（A1，A2，…，Am）有支配关系，可以建立以Ci为判断准则的元素A1，A2，…，Am间的两两比较判断矩阵A=（aij）max，见表10-8。
表10-8 两两比较判断矩阵
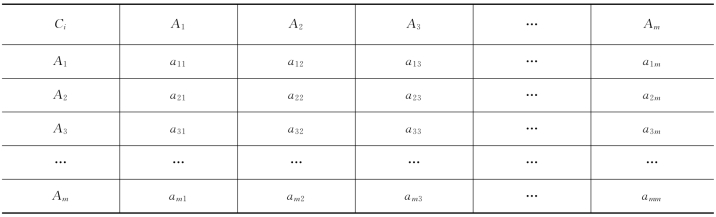
aij的含义是两因素比较的相对强度，一般用1～9标度，见表10-9。
表10-9 标度表
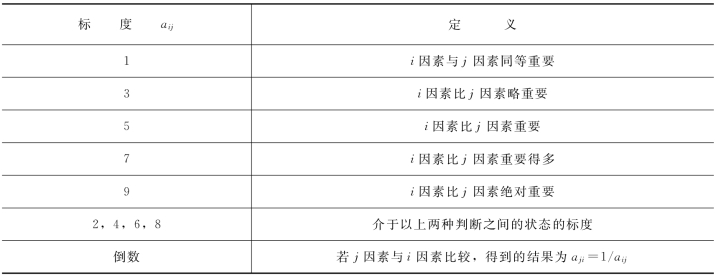
可知，若两因素同等重要，则aij=aji=1；若稍微重要，则aij=3、aji=1/3；若明显重要，则aij=5、aji=1/5；若非常重要，则aij=7、aji=1/7；若极其重要，则aij=9、aji=1/9；若重要性介于上述描述之间，则aij可取2、4、6、8，aji对应得到1/2、1/4、1/6、1/8。
四、单准则排序
单准则排序是通过计算判断矩阵，求解下一层各元素针对上一层某一元素的相对权重，这一过程是针对1个元素所进行的排序。针对上一层所有元素Ci，下一层元素A1，A2，…，Am两两比较得到判断矩阵A，解特征方程
计算最大特征根λmax，找出它所对应的特征向量W，即为同一层各因素相对于上一层各因素相对重要性的排序权重，然后进行一致性检验。所得向量W，经归一化及一致性检验后得到元素A1，A2，…，Am在准则Ci下的权重。
λmax、W的计算和判断阵矩的一致性检验。采用根法计算λmax和W，其计算步骤如下：
（1）A的元素按行相乘。
（2）所得的乘积分别开m次方。
（3）将方根向量归一化得排序权重W。
（4）按下式计算λmax：
（5）计算一致性指标CI：
（6）计算一致性比例CR：
式中 RI——平均随机一致性指标，由表10-10查取；
表10-10 平均随即一致性指标
m——平均判断矩阵的阶数。
当CR＜0．1时，一般认为判断矩阵的一致性可以接受。
五、层次总排序
把在单排序的基础上，计算每一层次中各个元素相对总目标的综合权重，并进行综合判断一致性检验的过程叫作层次总排序，即根据层次之间元素的所属或者支配关系，将各因素层的权数按照上下层元素的对应关系，逐层把对应的权重传递下来。
假设已计算出（k-1）层m个元素相对于总目标的排序权重向量为
第k层n个元素以第（k-1）层第m个元素为准则的排序权重向量为
令p k=（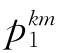
，
，…，
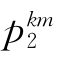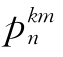），表示k层所有元素针对（k-1）层每1个元素的排序，这是1个m×n的矩阵，则第k层元素对总目标的合成排序为
【例10-7】层次分析法（AHP）是对非定量事件作定量分析的一种有效方法。新疆夹河子水库是拦河水库，其泥沙淤积严重，淤积量以每年80万～100万m3递增，有效库容逐年递减，目前淤积量已超过4200万m3，调节库容的有效水量只有3050万m3，加之洪水来临前又是灌区用水高峰期，还要保证东西2个灌区的用水平衡，所以库容就不能降得太低，只能尽可能降低到一定限度，同时须掌握来水情况，随时调整库容，在夹河子水库洪水调度系统中采用层次分析方法进行分析。
解：水库洪水调度系统的目标层为系统综合得分，准则层包括基础工作、经常性工作、洪水预报和洪水调度，指标层则对各项划分得比较细致，由此归纳出系统层次结构模型，见表10-11。
表10-11 新疆夹河子水库洪水调度系统层次结构模型
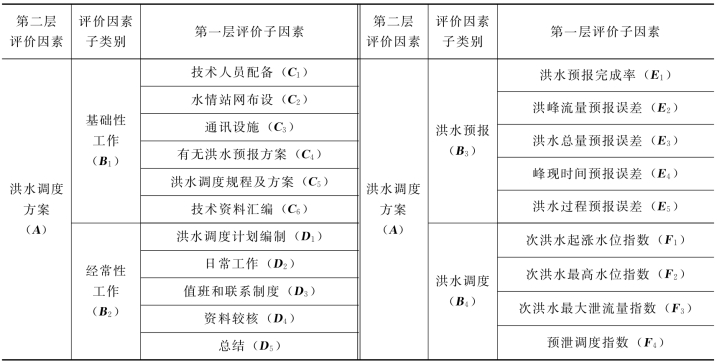
求判断矩阵，进行层次单排序。
判断矩阵A-B：
判断矩阵B1-C：
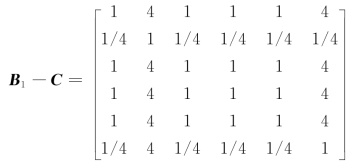
判断矩阵B2-D：
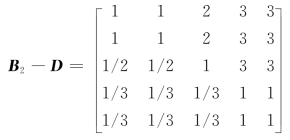
判断矩阵B3-E：
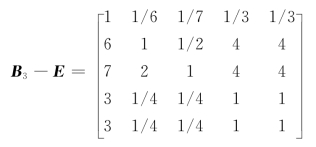
判断矩阵B4-F：
进行层次单排序：
有
计算判断矩阵的一致性指标CI=（λmax-n）/（n-1），随后还需要确定判断矩阵的平均随机一致性指标RI。1～9阶矩阵RI的取值见表10-12。
表10-12 以符合一致性检验中矩阵不同阶数RI的取值
当判断矩阵的随机一致性比例CR=CI/RI＜0．01时，认为判断矩阵具有满意的一致性。在判断矩阵B-F中，CI=0．01233，RI=0．90；CR=CI/RI=0．0137。因为CR＜0．10，所以符合一致性检验。
对判断矩阵B4-F，使用方根法计算过程如表10-13所示。
表10-13 方根法计算过程
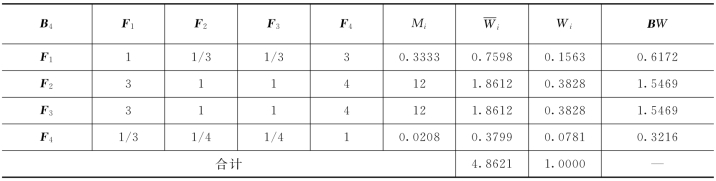
对其他4个判断矩阵进行计算，结果见表10-14，夹河子水库洪水调度方案评价的层次总排序。
表10-14 夹河子水库洪水调度方案评价的层次总排序计算表
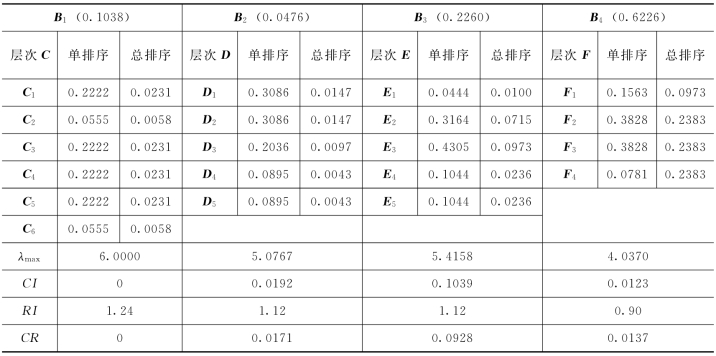
进行一致性检验：
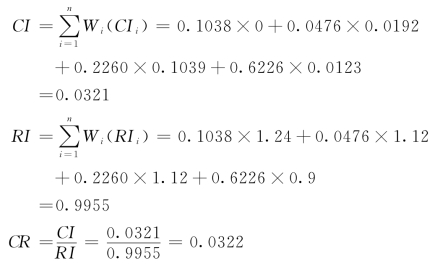
可以知道，满足一致性要求。
水库洪水调度方案综合评价是基于评价过程的非线性特点而提出的，对非线性的评价进行量化综合，从而得到可比的量化评价结果的过程。对基础工作和经常性工作各项指标进行定性评价并打分，评价结果包括好、一般和差3级，规定好对应的分数为80，一般对应的分数为60，差对应的分数为45，由此可得到各项指标的得分。
对洪水预报和洪水调度采用定量评分时，由于所用指标众多，彼此之间可比性差，为此对每一指标都进行标准化：
将其化为0～100的数值，以便进行比较和计算。利用公式
可以得到洪水调度总的评分值，根据此分值就可以判断洪水调度方案的合理度。