质量管理的几种工具
一、排列图
排列图又称ABC分类控制法，它最早是由意大利经济学家巴雷特（Pareto）发明，所以又称为巴氏图或巴雷特图。排列图是一种寻找影响质量主次因素的方法，所以也称为主次因素图。
巴雷特于19世纪把排列图用于经济管理领域。他通过对当时欧洲社会财富分布状况的调查分析，发现在资本主义社会中，大量的社会财富被少数人占有，而多数人仅占有社会少量财富。于是，巴雷特提出所谓“关键的少数和次要的多数”的关系。他依据统计数据画成了排列图，图中的曲线直观地显示出这种想像。
后来人们发现经济管理其他领域也存在着这种不均匀地规律，如在仓库、物资管理和价值工程中的ABC法，就是利用了排列图的原理。
美国质量管理专家朱兰（J．M．Juran）把巴雷特的这个原理应用到工业产品的质量管理中。1978年，我国引进全面质量管理方法时，排列图方法也就开始运用起来。
排列图方法就是用“关键的少数，次要的多数”的原理，对数据进行分类，排列作图，以直观的方法，表现质量的关键问题所在，表明应从哪里采取措施，经济效果最好。
（一）排列图的形式与分析
1．排列图的形式
排列图有两条纵坐标，一条横坐标和一条曲线所组成。
（1）左边的纵坐标表示频数，是各种影响质量的因素出现的次数。
（2）右边的纵坐标表示累计频数（百分率），是影响质量因素的累计频数。
（3）横坐标表示影响质量的各种因素，按影响程度的大小由左向右排列。
（4）每一个影响质量因素都用一个矩形表示，矩形的厚度表示影响质量因素的大小。
（5）曲线表示各种影响质量因素的累计百分数，称为巴雷特曲线或巴氏曲线。
排列图的基本形式如图15-2所示。
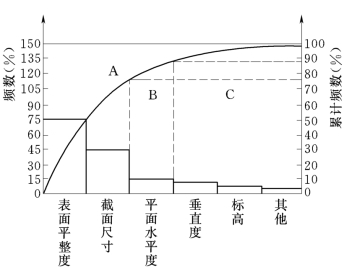
图15-2 构件尺寸不合格点排列图
（6）标出A、B、C三类的区间。
2．排列图的分析
通常将占累计百分数（累计频数）80%左右的项目称为主要因素，在累计频数为0～80%范围的区域称为A类区。
B类区的项目占总频数的10%左右，即累计频数在80%～90%范围，此区域内的因素称为次要因素。
C类区的项目占总频数的10%左右，即累计频数在90%～100%范围，此区域的因素称为一般因素。
在实际应用中，这种划分不是绝对的。有时占60%左右的项目也可以是主要因素，有时要看相邻直方间拉开的距离的大小，和考虑措施的难易，再确定主次因素。
（二）排列图的绘制
结合砌砖工程质量管理介绍排列图的应用。
1．检查测试，收集数据
首先根据《工程施工及验收规范》的规定，对有关项目进行检查测试，然后把收集到的数据按不合格数的大小排列，计算各自的频数和累计频数，见表15-1。
表15-1 项目不合格点统计计算表
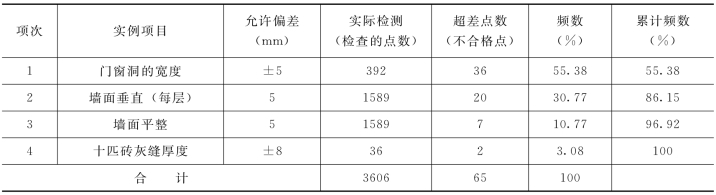
2．绘制步骤
（1）画坐标，定刻度。纵坐标与横坐标的长度之比一般是1∶2～2∶1。左纵坐标是频数坐标，底标原点为0，在合适的高度定出总格频数，一般总格频数比最大影响因素的频数大就可以了，也可按总频数作为总格频数，如本例中的65，然后均匀的标出一定整数点的刻度。右纵坐标是累计频数坐标，坐标原点为0，一般在与左纵坐标的总频数对应等高处定下100%刻度，然后均匀标出各控制点刻度。
横坐标标出项目刻度，项目刻度可将横坐标占完，也可画出一部分。
（2）按项目频数画出直方，如门窗洞的宽度的频数是36，从左纵坐标找到36数值，按这个高度，画出该项目直方，依次类推，画出各项目直方。
（3）画出巴雷特曲线，以各项目直方的右侧边线（或其延长线）为纵线，以项目累计频数引出的平行于横轴的横线为水平线，两线相交点处即为有关项目的累计频数。如在本例中“门窗洞口”和“墙面垂直”两项目的累计频数为86．15%，把各点用折线连接起来，就成为巴氏曲线。
（4）划分A、B、C类区，根据具体情况，定出A、B、C类区的累计频数，然后从右纵坐标向左纵坐标引平行于横坐标的坐标，然后标出A、B、C三类区，一般属于A类区的项目直方打阴影表示。
（5）必要说明，在图的下方填写排列图的名称、收集数据的时间、绘制者、分析结论等。本例结论是：造成该工程砌砖工程质量缺陷的主要因素是“门窗洞口的宽度”和“墙面垂直”，它们占不合格点数的86．15%，要提高砌砖工程质量，首先应在这两个项目上采取措施。
二、因果（分析）图
排列图找出主要质量问题所在，如要解决这些主要问题，必须找到造成这些问题的原因，以对症下药，达到解决问题的目的。因果图就是提供寻找质量问题原因的简便有效方法之一。
因果图为日本石川馨教授所创，1953年在日本川奇制铁公司茸合工厂首先应用。日本人常称为特性要因图或石川图。由于因果图的形状像树枝和鱼刺，又俗称树枝图、鱼刺图。
（一）因果图的形式
因果图是表示质量特征（果）和原因关系的图，是一种逐步深入研究和讨论质量问题的图示方法，如图15-3所示。
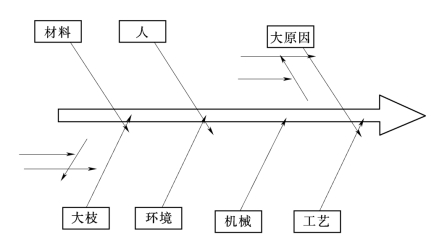
图15-3 因果图
在实际生产和施工过程中，任何一种质量问题的产生，往往是多种原因所造成的。把这些原因按照大小顺序分别用主干、大枝、中枝、小枝等图形表示出来，即为因果分析图。
它的作用是可以一目了然地系统观察出产生质量问题的原因，便于向领导汇报工作，研究对策，改进工作，从而达到控制质量的目的。
一张因果分析图是由若干枝干组成的，这些枝干就是从特征（果）到原因之间的网络，这些大大小小的枝干表示影响质量的大大小小的原因，它们之间的联络关系如图15-3所示。
产品质量的好坏是生产过程中许多原因的结果，但不外乎是人、材料、方法（工艺）、机械（设备）、环境五大因素。
（1）人（操作者）的因素，包括他的思想素质、身体素质和技术水平等。
（2）材料的因素，包括原材料、辅助材料、半成品和成品的质量因素。
（3）工艺（方法）的因素，包括施工程序、施工工艺以及操作方法等因素。
（4）机械（设备）的因素，包括各种施工机械、机具的质量因素。
（5）环境因素，包括操作环境、地区特点、气候特点等因素。
（二）因果图的绘制
1．确定要解决的问题
首先要明确分析的质量问题，即要解决的质量特性。如混凝土强度不足、地基处理质量不合格。本例要解决的问题是混凝土裂缝，画主干表示。
2．召开有关会议，提出产生问题的原因
召集同该质量问题有关的人员参加会议，会议应创造一个充分发扬民主、各抒己见、集思广益的气氛。
3．分析原因，作图表示
根据所提出的造成质量的原因，按照五大因素进行分类（也可根据具体性工艺进行综合或侧重）并且根据分层的原理，先后确定出大原因、中原因、小原因等，分解的程度应能便于判定解决质量问题的具体措施。这些原因根据从属关系，分别用长短不等的符号表示。
4．显示关键原因
对于影响质量较大的原因，要突出显示。所谓“影响较大”的原因不一定是“大原因”，有的小原因可能对“果”产生较大影响。
5．必要说明
在图上应注明本图的名称、绘制日期、绘制者、其他必要说明等。
图15-4表示混凝土强度不合格的原因分析，其中，第一层面从人、机械、材料、施工方法和施工环境进行分析；第二层面、第三层面、……，依此类推。
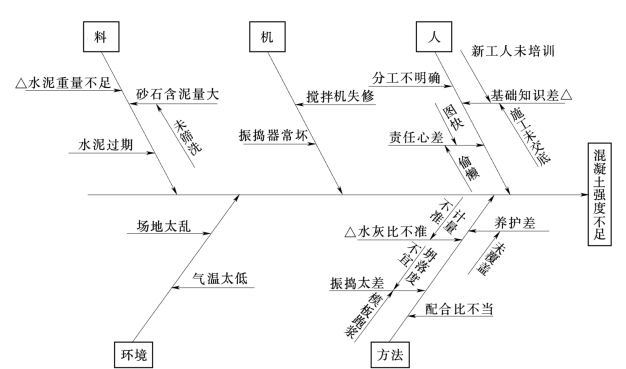
图15-4 混凝土强度不合格因果分析
三、直方图
产品质量总是有波动的。波动有两种类型：一种属正常的波动；另一种属于不正常的波动。波动的原因总是来自上述的五大因素。对于正常的波动（在正常范围内）是允许的，而对于不正常的波动则是不允许的。正常波动一般是有规律的运动，不正常的波动往往无规律。但是往往这两种波动混在一起出现，不易区别。要控制质量必须将两者分开来，用数理统计的方法，可以找出正常波动的规律，以此作标准，则不正常的波动也就区别开来了。
用数理统计方法寻找正常波动规律的方法之一就是作直方图，用直方图可以粗略估计出正常波动规律。
直方图法是在质量管理中用来整理数据、判断和预测生产过程质量的一种常用、简单而效果又比较好的工具，它是用来分析和判断生产过程是否稳定的一种图解。
直方图也称为频数直方图和质量分布图。对从一个母体收集来的一组数据用相同的组距进行分组，画出宽度为组距，高度为分组区间内数据出现的频数直方柱，按组界值（区间）的顺序把这些直方柱排列在直角坐标系里，这样得到的一系列直方柱组成的图形就是频数分布直方图。
直方图适用于计量值的数据。
（一）直方图的作法
1．收集数据
将收集的数据填入数据表内，作直方图所需的数据要大于50个，否则反映分布的误差太大，常用100～200个数据，数据总个数用n表示。
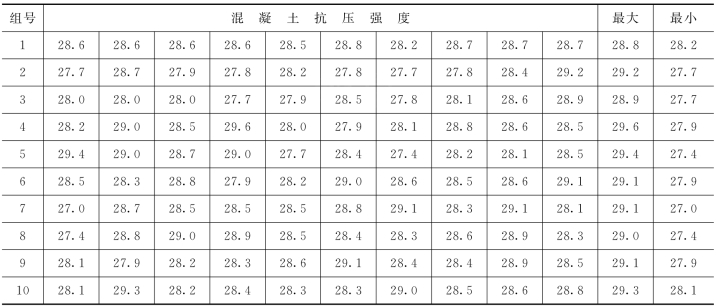
本例中取100组混凝土试块抗压强度平均值数据100个。n=100，可以认为n是充分大的，强度实例数据见数据表。
2．找出最大值和最小值，计算极差R
极差是表示全体数据的最大值和最小值之差，也就是全体数据的分布极限范围。
从数据表15-2中知：最大值Xmax=29．6，最小值Xmin=27．0，则极差为
表15-2 混凝土抗压强度数据表 单位：N/mm2
R=Xmax-Xmin=29．6-27．0=2．6（N/mm2）
3．确定分组数K
将数据的数值分布范围划分若干区间，称为分组。分组的数目要适当，数太少会掩盖组内数据变动情况，且会引起较大的计算误差；数太多会造成各组的高度参差不齐，而难以看清分布情况，得不出简单规律，且计算工程量大。组数K的确定可以参考表15-3，也可用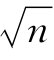
来表示。
表15-3 确定组数参考表
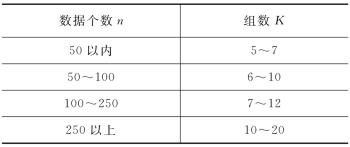
本例取K=10。
n=100 Xmax=29．6 Xmin=27．0
R=Xmax-Xmin=29．6-27．0=2．6（N/mm2）
4．确定组距h
组与组之间的间距，称为组距。用下式计算：
h=R/K
在本例中，h=2．6/10=0．26（N/mm2），取h=0．3，便于分组。
5．确定组界值（组的边界、分点）
确定组界值，就是找每组的起止点，使每组停止点与起点之差是组距h。
决定组界值的原则主要是不使数据漏掉和出现在边界上，所以通常取测定单位的1/2作为边界值的单位。
同时分组的范围应能把数据表中最大值和最小值包括在内，且最大值和最小值相同的第一组和最后一组的两端组界的间隔大致相等。
根据以上原则和要求，第一组下界限值X1下=Xmin-h/2。注意：当h为偶数时，这个公式不能用，因为可能某些数据正好落在边界值上。
还有一个h为奇数或偶数时都能使用的计算办法是
X1下=Xmin-最小测量单位/2
最小测量单位因不同的测量对象和计算手段而定。如人民币最小计算单位为1分，水泥重量为1kg，黄金为0．001g，混凝土强度为1N/mm2。
本例中
X1下=27．0-0．3/2=26．85
第一组上界限值为其下界限值加上组距。即
X1上=X1下+h
或 X1上=Xmin+h/2
本例中
X1上=26．85+0．3=27+0．3/2=27．15
第二组的下界限值等于第一组的上界限值，第二组的上界限值等于X1下+h，以此类推，定出各组的组界。
但到第K组时，Xmax值必须在第K组内，否则就增加一组，变成K+1组，但不必重复计算h值。
6．编制频数分布表
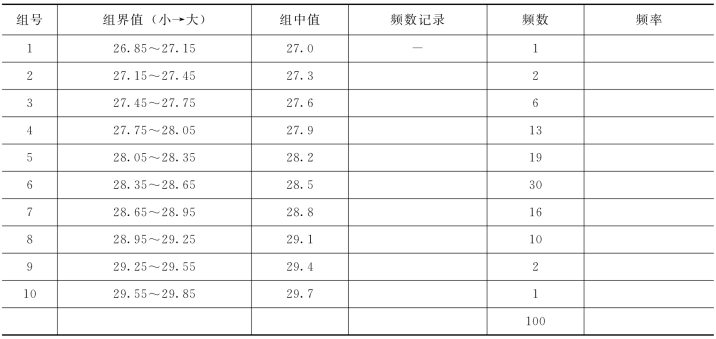
为了作直方图，要知道数据在各组内出现的次数，即统计各组的频数。频数分布表一般设有组号、组界值、组中值、频数记录、频数、频率等栏，见表15-4。需要注意的是，统计各组频数时容易出错，所以要细心认真。
表15-4 混凝土抗压强度频数分布表
7．作频数直方图
建立直角坐标系，横轴表示混凝土抗压强度，在横轴上标出各组的组界值；纵轴表示频数，以组距为底，以各组的频数为高，画出一系列矩形，这就是要画的直方图。
8．写出图名和其他必要说明
（二）直方图的观察分析
直方图能够比较形象、直观地反映产品质量的分布情况。使用直方图的主要目的之一，就是通过对图形的观察和分析来判断生产过程是否稳定。观察的方法是对图形的形状进行观察，并对照规格标准（公差）进行比较，对于异常形状的分布应判别异常的类型和原因。
1．对图形形状观察分析，可判断质量分布状态
有图形应着眼于直方图的整个形状，对图形中出现的局部一些参差不齐的形状，可不必太计较。常见的直方图类型形状有以下几种（见图15-5）：
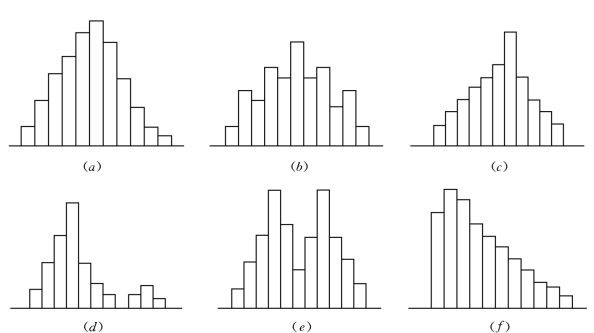
图15-5 常见的直方图
（a）正常型；（b）折齿型；（c）陡坡型；（d）孤岛型；（e）双峰型；（f）峭壁型
（1）正常型（对称型、正态分布型）。它的特点是中间高，两边低，左右基本对称，说明工序处于稳定状态。
（2）孤岛型。在远离主分布中心的地方出现小的直方群，形如孤岛。孤岛的存在说明在短时间内有异常因素在起作用，使工艺条件起了变化。如原料混杂、操作疏忽、不熟练工人替班、测量工具有误差等。
（3）偏向型（偏坡型）。直方的顶峰偏向一侧，计数值或计量值只控制一侧界限时，常出现这种形状，或是工作者有意想在某一方向留有余量而造成的。
（4）双峰型。这往往是由于把来自两个总体的数据混在一起作图所致。如两种工艺、两种设备、两组工人等。这属于分类不当造成的。
（5）平顶型（平峰型）。往往由于生产过程中有缓慢变化的因素在起作用，如设备的磨损、操作者的疲劳等。
（6）断齿型（锯齿型）。这种图形从整体看过去中间高，两边低，左右基本对称。但出现大量参差不齐的情况，造成这种情况不是生产中的问题，可能是分组过多或测量仪器精度不够，读数有误差等原因所致。
2．直方图与质量标准（规格标准）比较分析
当工序处于稳定状态时（直方图为正态分布型），还需进一步将直方图与规格标准进行比较，以判定工序满足标准要求的程度，如图15-6所示。
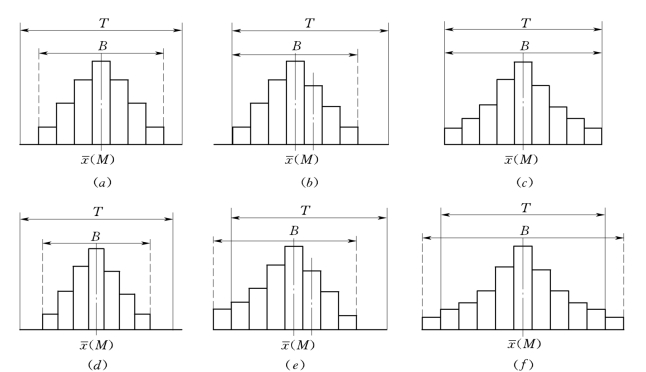
图15-6 直方图与质量标准上下限
注：B表示实际的质量特性分布宽度（范围）；T表示规格标准的界限（范围）T=Ta-Tc。
常见的直方图有以下几种：
（1）理想型。B在T中间，平均值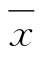
也正好与公差中心重合，实际尺寸分布的两边与标准的距离约T/8（即有一定的余地）。这样的生产过程不会出现什么问题。
（2）偏心型。显然分布范围落在公差界限之内，但分布中心偏离规格中心故有超差的可能，这个说明控制有倾向性。如工人在生产零件时，认为大了可能返工，小了则要作废，于是就往大的控制，要采取措施，调整中心。
（3）无实余型B=T。分布虽然落在规格范围之内，但完全没有余地，一不小心就会超差，要采取措施，减小数据的分散，缩小分布的范围。
（4）瘦型（显集型）T≫B。这种图形说明公差范围过分大于实际尺寸分布范围，质量过分满足标准的情况。虽然不出不合格产品，但太不经济。可以考虑改变工艺、放松加工精度、放宽公差标准，有利于降低成本。
（5）胖型（超差型）B＞T。实际分布的范围太大，造成超差。这是由于质量波动太大，工序能力不足，出现了一定量的不合格状态，应采取多方面的措施，使分布都在标准规格之内。
（6）陡壁型（绝壁型）。这是由于工艺控制不好，实际尺寸过分地偏离规格中心，造成超差或废品。但是在作图时，数据中已剔除了不合格品，所以超过规格线外的部分，可能是初检时的误差或差错所致。