模糊综合评价法
模糊综合评价是借助模糊数学的一些概念,对实际的综合评价问题提供一些评价的方法,它与概率、统计的方法是不同的。因为客观事物的不确定性有两大类:一类是事物对象是明确的,但出现的规律有不确定性,例如晴天、下雨、下雪,这是明确的,但出现规律不确定;另一类是事物对象本身不明确,例如年轻、年老、严重、不严重等这—类程度上的差别没有截然的分界线。
一、模糊数学基本概念
(一)模糊性
模糊性是指某些事物或概念的边界不清楚,这种边界不清的模糊概念,不是由于人的主观认识达不到客观实际所造成的,而是事物的一种客观属性,是事物的差异之间存在着中间过渡过程的结果。例如,关于地震的震级,飓风的强度,对某种质量的评定以及生活中区分青年、中年和老年等,由于评定事物的标准或事物本身的定义没有明确的“边界”,从而构成不确定性。
设给定实数域U,U到[0,1]任一映射μA
![]()
都确定了U上的一个模糊集合,习惯上称为模糊子集,U上的全体模糊子集构成的集合称为模糊幂集,记作F(U),这里μA叫做A的隶属函数,μA(μ)称为对A的隶属度,也记作
![]()
模糊子集完全由其隶属函数所刻划,特别地当值域取[0,1]的两个端点,亦即0,1两个值时,便退化为一个普通子集,隶属函数也就退化为特征函数。由此可见,普通集合是模糊集合的特殊情况,而模糊集合是普通集合的推广。这样,对于实数域U的一个元素u和U上的一个模糊子集A,我们不应简单地问u绝对属于还是绝对不属于A,而应问u在多大程度上属于A,隶属度μA(u)正是u属于A的程度的度量。
(二)隶属度与隶属函数
一般的,设X为一实数域,L为一模糊集合,若X的每一个元素都对应一个对L的隶属度,即存在一个映射
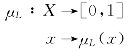
则称μL(x)为L关于X的隶属函数。
要对u0时候属于A,做n次模糊统计实验(如对“60岁的人”是否属于“老年人”作一次意见调查),我们就可以得出u0对A的隶属频率:
![]()
只要实验次数n足够大,该隶属频率就会稳定地趋于某一个值,这个值就称为u0对A的隶属度。记为最大隶属度原则:若有i∈{1,2,…,n},使
![]()
则认为u0相对隶属于A。
(三)模糊集合的内积、外积和贴近度
在模糊学里,∧、∨均为扎德算子,“∨”表示取最大,“∧”表示取最小,“°”为运算符,模糊矩阵的合成也称为Q对R的模糊乘积。
设实数域为U,A、B是U的模糊集合,称数值
![]()
为B的内积;称数值
![]()
为B的外积。
若A⊆B⊆C,则σ(A,C)≤σ(A,B)∧σ(B,C),σ称映射为U的模糊集合的贴近度。
(四)模糊矩阵
矩阵A=(qij)m×n称为模糊矩阵,如果对任意的i≤m及j≤n,都有aij∈[0,1]。
对于任意模糊矩阵A=(qij)m×n和B=(bij)m×n,A+B=(aij∨bij)称为A与B的和;A×B=(aij∨bij)称为A与B的叉积。符号a∨b表示在a与b中取较大的,a∧b表示在a与b中取较小的。如果aij≤bij(i=1,2,…,m;j=1,2,…,n),则称A小于等于B,记为A≤B。
设m行n列的模糊矩阵A和n行p列的模糊矩阵B分别为
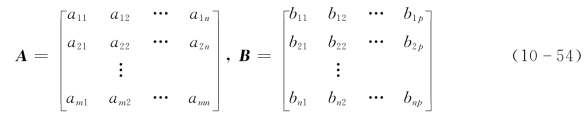
它们的乘积C为m行p列的模糊矩阵,即
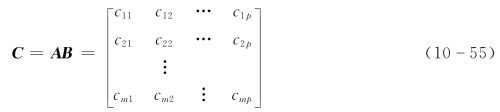
其中
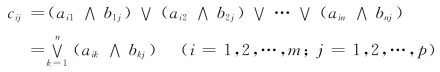
一个n行m列模糊矩阵Q=(qij)n×m,对一个m行l列的模糊矩阵R的合成Q°R为一个n行l列的模糊矩阵S,S的第i行第k列的元素等于Q的第i行元素与R的第k列元素的对应元素两两先取小者,然后再在所得的结果中取较大者,即
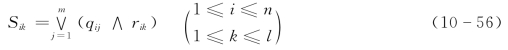
二、模糊综合评价法
(一)模糊综合评价法相关概念
模糊综合评价就是以模糊数学为基础,应用模糊关系合成的原理,将一些边界不清,不易定量的因素定量化、进行综合评价的一种方法。
模糊综合评价包含6个基本要素:评价因素实数域U、评语等级实数域V、模糊关系矩阵R、评价因素权向量A、合成算子、评价结果向量B。
(二)利用一级模型进行模糊综合评价
模糊综合评价就是一个模糊变换。其模型可分为一级和多级模型,其中一级模型是基础,如果要进行多级模型的分析,必须了解认识一级模型。
1.利用一级模型进行模糊综合评价的基本步骤
一级模型模糊综合评价包括六个基本步骤。
(1)确定评价对象的因素实数域U:
U=(u1,u2,…,un)
从社会经济统计的角度看,这一步就是要确定评价的指标体系,解决用什么指标和从哪些方面来评价客观对象的问题。
(2)确定评语等级实数域:
V=(v1,v2,…,vn)
这一步是其他多指标综合评价方法所没有的,也正是由于这一实数域的确定,才使得模糊综合评价得到了一个模糊评价向量,被评事物对应各评语等级隶属程度的信息通过这个模糊向量表示出来,体现评价的模糊特性。
从技术处理来看,评语等级个数m通常要大于4而不超过9,因为一方面,m过多不超9,m过多的语义区分能力,不易判断对象的等级归属,另一方面m过少又不合模糊综合评价的质量要求,故m过多过少都对评价结果有不良影响,以适中为宜。
(3)进行单因素评价,建立模糊关系矩阵R(隶属关系矩阵):
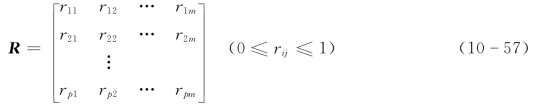
(4)确定评价因素权向量A。A是U中各因素对被评事物的隶属关系,它取决于人们进行模糊综合评价时的着眼点,即评价时依次着重于哪些因素。这一步与常规综合评价中各指标权数确定作用是相同的,但这里更明确强调所确定的A是一个模糊子集,即要求用模糊方法来确定权向量。
(5)选择合成算子,将A与R合成得到B。模糊综合评价的基本模型为B=A°R。这个公式表示评价因素与被评事物的模糊关系A通过模糊变换器R(R是评价因素与评语等级间的模糊关系),形成了被评事物与评语等级间的模糊关系B。
(6)对模糊综合评价结果B作分析处理。
2.单因素评价
模糊单因素评价方法与因素(指标)的属性有关,不同属性的因素可以采用不同的方法,这里介绍等级比重法、隶属函数法、频率法。
(1)等级比重法。主观指标反映了人们对客观事物的看法,如对住房内部装潢的欣赏程度,对桥梁是否安全的认识,在大洪水冲击下对水坝安全的认识程度等。用等级比重确定隶属关系矩阵R的方法,就是要人们从若干因素对其一事物属于哪个等级作出判断,然后把从某因素将该事物评判为某等级的人数在全部评判人数中的比重作为rij,就得到了隶属关系矩阵。比如对某水坝从工程造价、安全性、耐久性、可靠性4个方面评价,分为4级。
如表10-15所示,可以计算确定隶属关系矩阵R:
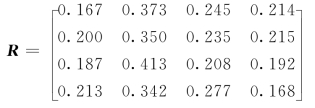
表10-15 某水坝调查评价数据
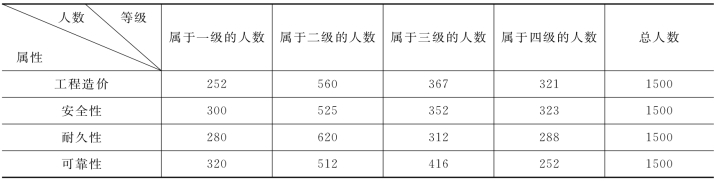
用等级比重法确定隶属度时,为了保证可靠性,一般要注意两个问题:
1)评价者人数不能太少,因为根据模糊统计试验,只有当试验次数n充分大时,等级比重才趋于隶属度。设W是一个实数域,F1表示工程造价,是W中的一个元素,同时定义W的一个子集合,显然,对于某一个人来说,H*是一个普通的集合,但是对于不同的人来说,H*可能是不相同的。因为不同的人判断F1是否属于H*,有时会得到F1属于H*,有时会得到F1不属于H*。因此,对一批评价者来说H*是W上一个运动的、边界可变的普通子集合,它就对应着一个模糊集合
H={属于一级的人数}
F1对H的隶属度可以表示为
![]()
式中 n——实验次数(这里为评价人员数)。
随着n的增大,比重趋于[0,1]中的一个稳定数,就是F1对H的隶属度。
2)评价者必须对被评事物有相当的了解,特别是一些涉及专业方面的评价。
(2)隶属函数法。从隶属函数人手确定隶属关系矩阵R的方法就是根据专业知识和样本资料分布情况,从已知的各种隶属函数中选取一个合适的公式并确定其中的参数,代入数据后求得rij。这种方法的困难之处在于要依次确定被评对象隶属于各个等级的隶属函数关系式。
客观或定量指标一般都有数值表现结果,如果能得到它们对等级模糊子集的隶属函数,求隶属度就非常方便了。从模糊学可以知道,隶属函数的分布主要有成上型、成下型和中间型三种,并且有一些具体的函数形式,因此实际评价中只需依据指标的特性和等级模糊集合选择一种合适的形式并确定其中参数即可。
(3)频率法。该方法是先划分指标值在不同等级的变化区间,然后以指标值的历史资料数据在各等级变化区间内出现的频率作为对各等级模糊子集的隶属度。
3.模糊权向量的确定
设因素实数域
U={u1,u2,…,up}
U上的模糊子集
M={对评价内容重要的因素}
因素ui对M的隶属度为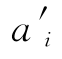 ,则模糊权向量为
,则模糊权向量为
A={a1,a2,…,ap}
其中
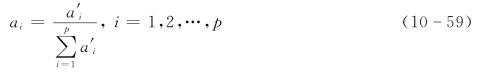
对模糊权向量的确定多采用专家估计法,即请几位专家分别估计出ui(i=1,2,…,p)对M的隶属度,然后对不同专家的估计结果求平均并归一就可以得到A。
4.选择模糊合成算子
模糊综合评价的原理是模糊变换

在模糊综合评判的基本公式A°R中,A与R如何合成,对综合判评结果有不小的影响。这里对几种常见的模糊合成算子的特点及其对模糊综合评判的适用性作一探讨。
常见的模糊合成算子有以下几种:
(1)M(∧,∨)算子:
![]()
(2)M(·,∨)算子:
![]()
(3)M(∧,⊕)算子。“⊕”是有界和运算,即在有界限制下的普通加法运算,对t个实数x1,x2,…,xt有
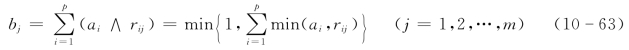
(4)M(·,⊕)算子:
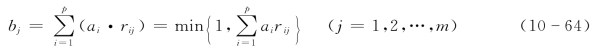
5.最大隶属原则有效度的测量
设模糊综合评价结果向量为B=(b1,b2,…,bm),如果br=![]() ,则被评事物总体上来讲隶属于第r等级,这就是最大隶属原则。
,则被评事物总体上来讲隶属于第r等级,这就是最大隶属原则。
定义
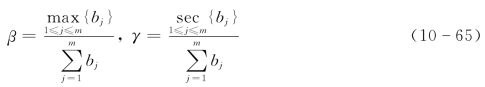
式中![]() ——B中最大分量;
——B中最大分量;
β——B中最大分量总和的比例,![]() ;
;
γ——B中次大分量总和的比例,![]() 。
。
定义
![]()
α越大,最大隶属度则有效度越高,因此可以用α指标对最大隶属度原则有效性进行度量。一般情况下α的不同范围对应的最大隶属原则的有效性情况,见表10-16。
表10-16 最大隶属原则的有效性情况表

6.加权平均原则
当α值较小,使用最大隶属原则低效时,就应考虑使用新的判别原则。这里提出加权平均原则来补充最大隶属原则的不足。
加权平均原则的基本内容是:以等级值aj作为变量(j=1,2,…,n),n和aj通常人为确定,如aj=(1,2,3,4,5);以综合评价结果bj作为权数,计算

式中 K——待定系数(K=1或K=2),目的是控制较大的bj所起的作用。
7.模糊向量单值化
如果给各等级赋以分值,然后用B中对应的隶属度将分值加权求平均就可以得到一个点值,便于比较排序。
设给m个等级依次赋以分值c1,c2,…,cm,一般情况下(等级是由高到低或由好到差),c1>c2>…>cm,且间距相等,则模糊向量可单值化为

式中 K——待定系数(K=1或K=2),目的是控制较大的bj所起的作用。
(三)利用多级模型进行模糊综合评价
利用多级模型进行模糊综合评价的一般步骤。
(1)将因素实数域按某种属性分成s个子集:
![]()
(2)对每个子集Xi利用一级模型分别进行模糊综合评价。
(3)进行多级模型综合评价。
对于利用多级模型进行模糊综合评价的方法比较复杂,这里就不进行详细的论述了。利用一级模型进行模糊综合评价方法和利用多级模型进行模糊综合评价方法不同之处在于多级模型将因素集U分成若干组:
![]()
设Ui={ui1,ui2,…,uimi},于是U={u11,…,u1m1,u21,…,up1,…,upmp},令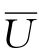 ={U1,U2,…,Up}称为
={U1,U2,…,Up}称为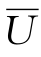 为第2层因素集,其元素
为第2层因素集,其元素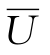 为第1层因素集U的子集。
为第1层因素集U的子集。
