互斥方案的选优
在工程技术经济分析中，较多的是互斥型方案的比较和选优问题。对于一组互斥方案，只要方案的投资额在规定的投资限额之内，均有资格参加评选。在方案互斥的条件下，经济效果评价包含两部分内容：一是考察各个方案自身的经济效果，即进行绝对效果检验；二是考察哪个方案最优，即相对效果检验。两种检验的目的和作用不同，通常缺一不可。
互斥方案的比较可按各个方案所含的全部因素（相同因素和不同因素）计算各方案的全部经济效益，进行全面的对比；也可仅就不同因素计算相对经济效益，进行局部的对比；前者是通用的比较方法，即全面比较法。对于以上所述的评价方法与所用的评价指标如表11-1所示。
表11-1 互斥的评价方法与评价指标
传统的工程经济学著作强调产出的数量、质量、时间等方面的可比性，为此要进行繁杂的等同化处理，随着经济体制的改革和市场经济的发展，产出的数量和质量都可以通过市场价格和销售收入体现出来。无论是成本降低，还是质量提高，或者产量增加，所有这一切均表现为利润（税收）的增加。因此本书只考虑互斥型方案的时间可比性问题。把互斥方案的选择根据各方案寿命期是否相等分为两部分：一是各方案寿命期相等；二是各方案寿命期不全相等。
一、寿命期相等方案的比较与选择
对于寿命期相等的互斥方案，通常将方案的寿命期设定为共同的分析期，这样，在利用资金等值原理进行经济效果评价时，方案间在时间上才具有可比性。在进行寿命相同方案的比较和选择时，若采用价值性指标，则选用价值性指标最大者为最优；若采用比率性指标，则需要考察不同方案之间追加投资的经济效益。
（一）净现值法
在进行多方案比选时，现值法可以分为单独分析和增量分析2种方法。
1．单独分析法
此方法是多方案比选中最常用的方法。
（1）净现值法。可以计算各个备选方案的净现值，检验各个方案的绝对经济效果。去掉NPV＜0的方案，然后对绝对经济效果合格的方案，比较其净现值，以净现值最大的方案为最优方案。
【例11-1】对于某工程有两个独立方案甲和乙，甲方案第一年投资300万元，每年可收入50万元，寿命期为50年；乙方案第一年投资400万元，每年可收入60万元，寿命期为60年，试比较两方案的经济性（基准折现率为10%）。
解：按照计算步骤进行计算。
NPV甲=-300+50（P/A，10%，50）=-300+50×9．915=195．75（万元）＞0
NPV乙=-400+60（P/A，10%，60）=-400+60×9．967=198．02（万元）＞0
两方案本身在经济上都是可行的。
由于NPV甲＜NPV乙，因此选择乙方案。
（2）内部收益率法。所谓内部收益率法，就是以内部收益率为比较基准，来进行评价的方法。内部收益率是反映投资使用效率的指标，是测定资金利用情况好坏的指示器。通过各方案内部收益率的计算和比较，内部收益率最高的方案，应是诸方案中经济效果最优的方案；内部收益率大于或等于折现率的方案，就是可以被采纳的方案。内部收益率法是与净现值法本质上不同的另一种评价方法，它着眼于资金利用的好坏，而非所得绝对效果的大小。
【例11-2】对于某工程有两个独立方案甲和乙，甲方案第一年投资200万元，每年可收入39．1万元，寿命期为10年；乙方案第一年投资160万元，每年可收入32万元，寿命期为10年，试用内部收益率法进行多方案选优（基准折现率为10%）。
解：先计算各个方案的内部收益率。
对甲方案，由公式
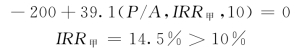
对乙方案，由公式
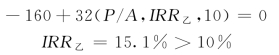
由于两者均大于10%，故方案甲、乙均是可行方案。
由于IRR甲＜IRR乙，则选择乙方案。
2．增量分析法
（1）差额净现值法。两个互斥方案之间现金流量之差（通常为投资额较大方案的现金流量减去投资额较小方案的现金流量）构成新的现金流量，称为差额现金流量。例如，我们可以将A方案与B方案的差额现金流量作为一个新的方案，称为差额方案（B-A），这一新方案的含义是B方案比A方案多投资，而B方案每年净收益比A方案多2万元，如图11-3所示。
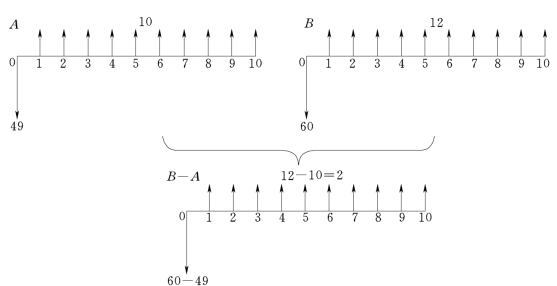
图11-3 差额现金流量与差额方案
如果备选方案各年的净现金流量无法估量，但可以估算出两个对比方案之间的差额指标值，此时用增量分析法来比选方案就更为方便。增量分析法一般采取两两比较的环比方式，但当方案数目较多时，这种比较就过于繁琐
。这时，可采取如下简化步骤减少比较次数：①将各方案按投资额大小排序；②计算各方案的绝对经济效果指标考察经济合理性，选投资额最小的合理方案为临时最优方案；③依次计算其余方案相对于前一步骤中的最优方案的经济指标，优胜劣汰，得到最终优选方案。评价指标可根据情况选用差额净现值ΔNPV。
设A、B是有共同寿命期n年的两个互斥的投资方案，B方案比A方案投资大，两方案的增量投资（差额）净现值可由下式得出：
式中 ΔNPV一一一差额净现值；
（CI-CO）2一一一投资大的方案的净现金流量；
（CI-CO）1一一一投资小的方案的净现金流量；
ΔCI一一一ΔCI=CI2-CI1；
ΔCO一一一ΔCO=CO2-CO1。
若ΔNPV＞0，则表明投资大的方案优于投资小的方案；若ΔNPV＜0，则选择投资小的方案。如果被比较的两个互斥方案的投资为期初一次投资，各年的现金流量为等额系列收支时，差额净现值的计算公式可简化为
式中 ΔK一一一两方案的投资差额：
ΔR一一一两方案的收益差额。
差额净现值法可用来检验差额投资的效果，即增加的那部分投资是否合理，但不能表明全部投资是否合理。因此，在运用差额净现值法时，首先必须确定作为比较基准的方案的绝对经济效果是好的。
一组互斥方案可按下列程序采用差额净现值法比较选择最优方案。①将互斥方案按投资额从小到大的顺序排序；②增设0方案（0方案又称为不投资方案或基准方案，其投资为0，净收益也为0），选择0方案的经济涵义是指不投资当前的方案，投资者就不会因为选择当前投资方案而失去相应的资金的机会成本（基准收益率），在一组互斥方案中增设0方案可避免选择一个经济上并不可行的方案作为最优方案；③将顺序第一的方案与0方案以差额净现值法进行比较，以两者中优的方案作为当前最优方案；④将排列第二的方案再与当前最优方案以差额净现值法比较，以两者中优的方案替代为当前最优方案；⑤以此类推，分别将排列于第三、第四、……的方案分别与各步的当前最优方案比较，直至所有的方案比较完毕；⑥最后保留的当前最优方案即为一组互斥方案中在经济上最优的方案。
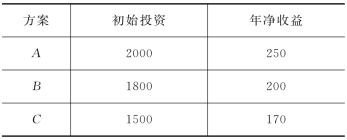
【例11-3】存在3个互斥方案（见表11-2），A方案：初始投资为2000万元，年净收益为250万元；B方案：初始投资为1800万元，年净收益为200万元；C方案：初始投资为1500万元，年净收益为180万元（已知3个方案的投资寿命期均为50年；ic=10%）。
表11-2 方案投资收益表 单位：万元
解：由题意，计算净现值：
NPVA=-2000+250（P/A，10%，50）=-2000+250×9．9148=478．70（万元）
NPVB=-1800+200（P/A，10%，50）=-1800+200×9．9148=182．96（万元）
NPVC=-1500+170（P/A，10%，50）=-1500+170×9．9148=185．52（万元）
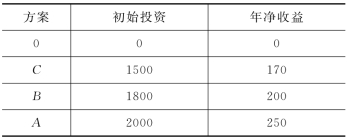
增设0方案（见表11-3），投资为0，净收益也为0，按投资额从小到大的顺序排序，顺序如下：（0，C，B，A）。
表11-3 调整顺序后项目投资收益表 单位：万元
将C方案与0方案以差额净现值法进行比较：
ΔNPVC-0=NPVC=478．70（万元）
则C方案为当前最优方案。
将B方案与C方案以差额净现值法进行比较：
ΔNPVB-C=-200+50（P/A，10%，50）=-200+50×9．9148=295．74（万元）
则B方案为当前最优方案。
将B方案与A方案以差额净现值法进行比较：
ΔNPVA-B=-300+30（P/A，10%，50）=-300+30×9．9148=-2．56（万元）＜0
则B方案为当前最优方案。
综上所述，A、B、C三个方案进行分析比较可知B方案为最优方案。
（2）差额内部收益率法。内部收益率是一个重要且常用的动态评价指标，但在用于方案比较时，用内部收益率指标进行方案比较，有时会出现与净现值指标比较不同的结论。差额内部收益率是指使得两个互斥方案形成的差额现金流量的差额净现值为0时的折现率，又称为增额投资收益率，用符号ΔIRR表示。设两个互斥方案j和k，寿命期皆为n，第t年的净现金流量分别为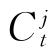
和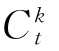
（t=0，1，2，…，n），则ΔIRRk-j满足下式
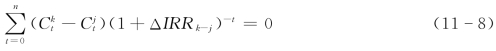
根据ΔIRR的概念及差额现金流量和IRR所具有的经济涵义，ΔIRR数值大小表明了下面几方面的经济涵义：
若ΔIRR=ic时，表明投资大的方案比投资小的方案多投资的资金所取得的收益恰好等于既定的收益率（基准收益率）；
若ΔIRR＞ic时，表明投资大的方案比投资小的方案多投资的资金所取得的收益大于既定的收益率；
若ΔIRR＜ic时，表明投资大的方案比投资小的方案多投资的资金的收益率未能达到既定的收益率。
【例11-4】题目同[例11-2]，试用差额内部收益率法进行比较与选择。
解：增设0方案，投资为0，净收益也为0，按投资额从小到大的顺序排序，顺序如下：（0，乙，甲），见表11-4。
表11-4 调整顺序后项目投资收益表
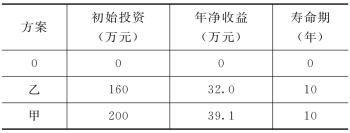
将乙方案与0方案以差额净现值法进行比较：
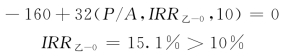
则乙方案为当前最优方案。
将甲方案与乙方案以差额净现值法进行比较：
则甲方案为当前最优方案。
由上可知甲方案为最优方案。
二、寿命期不等方案的比较与选择
实际工作中，相互比较的备选方案的服务寿命常常是不同的，在时间上不具有可比性。因此，在进行方案评选时，必须首先解决各方案寿命不同的问题，然后再依照寿命相同互斥方案的评选办法比较方案优劣。解决服务寿命不同的方法通常有以下四种：
（1）取各备选方案服务寿命的最小公倍数作为各方案比较的共同服务年限。在此期间内，当某方案服务寿命终结时，继续用同一方案更替。
（2）取寿命最短的服务寿命作为各方案比较的共同服务年限。这样，服务寿命长的方案在共同服务年限期末仍具有一定的“未使用价值”，应予以回收。
（3）取寿命最长方案的服务寿命为各方案比较的共同服务年限。这样，服务寿命短的方案在其服务寿命终结时，继续以同一方案更替直到共同服务年限期末为止。这时，共同服务年限期末可能也具有一定的“未使用价值”，应予以回收。
（4）按具体情况规定统一的服务年限。这样在达到统一服务年限前，服务寿命短的方案以同一方案重复。这时，在统一服务年限期末可能具有“未使用价值”，应予以回收。
以下分类举例来进行说明。
（一）方案重复法（最小公倍数寿命法）
该方法以不同方案的寿命期的最小公倍数为研究周期。假设各方案在此期间重复投资，计算出各方案的经济指标（一般是净现值）进行比较选优。
【例11-5】某建筑单位拟选择方案A、B、C，其寿命期不同，净现金流量如表11-5所示，试进行多方案选优（已知：ic=10%）。
解：由表11-5数据可得3个方案的最小公倍数为120年，可以得出：A方案重复4年，B方案重复2年，C方案重复3年，如图11-4所示。
表11-5 各方案现金流量
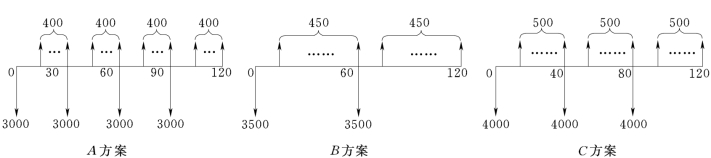
图11-4 各方案现金流量示意图
从以上的计算结果可得NPVB＞NPVC＞NPVA。
经过比较，选择B方案。
当然，不是所有的都可重复实施。如一些不可再生资源的开发，在进行寿命期不等的互斥方案比选时，不能用含有方案可重复假定的年值法和现值的最小公倍数法，可以直接按方案各自寿命期计算的净现值进行比选。其隐含的假定是寿命期短的方案在寿命期结束后，所投资金按基准折现率取得收益。
此法也称最小公倍数法或方案重复法，即把比较的方案重复实施，直到各个方案的期限为止。显然，这个相等的计算期就是诸方案的最小公倍数。应用这个方法时至少应当满足以下条件：
（1）对各个方案的需要期较长，至少不应短于最小公倍数年限。
（2）方案可以不改变其现金流量（投资、效益和费用都保持不变）而反复实施若干次。
这个方法存在的缺点如下：
（1）计算繁琐，将问题复杂化了，解决此问题可采用净年值法，也即在各寿命期不等前提下将各现金流量等值折算到寿命期，以此作比较。
（2）往往和工程实际分不开。
（二）净年值法
在对寿命期不等的互斥方案进行比选时，净年值法是最为简便的方法，当参加比选的方案数目众多时，尤其如此。
设m个互斥方案的寿命期分别为n1，n2，…，nm，方案j（j=1，2，3，…，m）在其寿命期内的净年值为
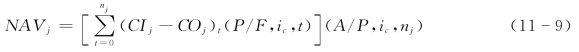
净年值法的判别准则为净年值大于或等于0且净年值最大的方案为最优可行方案。用净年值法进行寿命期不等的互斥方案进行比选，实际上隐含着作出这样一种假定：各备选方案在其寿命结束后均可按原方案重复实施或以与原方案经济效果水平相同的方案持续。因为一个方案无论重复实施多少次，其净年值是不变的，所以，净年值法实际上假定了各方案可以无限多次重复实施。在这一假定前提下，净年值法以“年”为时间单位比较各方案的经济效果，从而使寿命期不等的互斥方案具有可比性。
（三）无穷大寿命法
如果几个方案的最小公倍数寿命数值很大，则上述计算非常麻烦。方案重复法是将被比较的方案的一个或几个重复若干次或无限次，直至各方案期限相等为止。显然，这一相等期限就是各方案寿命的最小公倍数或无穷大寿命。前者可称为最小公倍数法，后者可称为无穷大寿命法。
（四）研究期法
研究期法的定义是针对寿命期不同的互斥方案，直接选取一个适当的分析期作为各个方案共同的计算期，通过比较各个方案在该计算期内的净现值来对方案进行比选。以净现值最大的方案为最佳方案。这里研究期的选择没有特殊的规定，但显然以诸方案中寿命最短者为研究期，计算最为简便，而且完全可以避免重复性假设。不过需要指出的是，研究期法涉及寿命期未结束方案的未使用价值的处理问题。其处理方式有三种。
（1）承认方案未使用价值。
（2）不承认方案未使用价值。
（3）预测方案未使用价值在研究期末的价值并作为现金流入量。在实际应用中，比较合理的方法是对计算期以后的现金流量进行合理的估算，这样才能保证比选结论的合理性。