不确定性分析方法
我们分析各种不同因素对方案经济效果的影响,采用了不确定性分析方法,以下我们要对盈亏平衡分析法、敏感性分析法及概率分析法进行阐述。
一、盈亏平衡分析法
(一)盈亏平衡分析法的定义
工程的盈亏平衡分析是根据正常生产年份的产品产量(或销售量)、可变成本、固定成本、产品价格和销售税金等数据,确定的盈亏平衡点BEP,即盈利为0时的临界值,通过BEP(盈亏平衡点)分析的成本与收益的平衡关系的一种方法。它也是在工程不确定性分析中常用的一种方法。
盈亏平衡点是盈利与亏损的分界点,它标志着不盈不亏的生产经营临界水平,反映在一定的生产经营水平时工程的收益与成本的平衡关系。盈亏平衡分析的主要目的在于通过盈亏平衡计算找出和确定一个盈亏平衡点,以及进一步突破此点后增加销售数量、增加利润、提高盈利的可能性。盈亏平衡分析还能够有助于发现和确定企业增加盈利的潜在能力以及各个有关因素变动对利润的影响程度。
(二)单方案盈亏平衡分析
单方案盈亏平衡分析,是通过分析产品产量、成本和盈利能力之间的关系,找出方案盈利与亏损在产量、单价、单位产品成本等方面的临界值,用来判断方案在各种不确定因素作用下的风险情况。由于单方案盈亏平衡分析是研究产品产量、成本和价格之间的关系,所以又称为本利分析。按照销售收入与销售量之间的关系,单方方案盈亏平衡分析可以分为线形盈亏分析和非线形盈亏分析。
1.线形盈亏平衡分析法
工程进行线形盈亏分析,必须满足以下条件:①生产单位按销售量组织生产,产品销售量等于产品产量。销售量不变,销售收入与产量呈线形关系,不会通过改变产品销售价格来增加销售量;②总成本是由固定成本和可变成本组成的,其中,固定成本稳定不变,可变成本随产量变化,变化趋势下文将进行讲述;③在分析期内,产品市场价格、生产工艺、技术装备、生产方法、管理水平等均无变化;④只生产一种产品,或当生产多种产品时产品结构不变,且都可以换算为单一产品计算。
(1)相关概念:
1)固定成本。固定成本也称“固定费用”,是变动成本的对称。固定成本是指在一定的范围内不随产品产量或商品流转量变动的那部分成本。固定成本大部分是间接成本,如企业管理人员的薪金和保险费、固定资产的折旧和维护费、办公费等。当产品产量或商品流转量的变动超过一定的范围时,固定费用就会有所增减。所以,固定成本只是一个相对固定的概念,我们称之为“相对固定成本”。
2)变动成本。变动成本是指成本总额随着产量的变动而成正比例变动的成本。这里的变动成本是就总产量的成本总额而言。若从单位产量的变动成本来看,它是固定的,即它不受产量增减变动的影响。
3)混合成本。混合成本是指介于固定成本和变动成本之间,其总额既随业务变动又不成正比例的那部分成本(电话费、设备的维护保养费用),即随着产量的变动,总额将发生与之相应的、变动幅度不等的变动的有关成本,加上设备维修费、检验人员工资等。混合成本可进一步区分为“半固定成本”和“半变动成本”。半固定成本指总额依次在不同产量水平上分别保持相对固定的有关成本。从全局考察,呈跳跃式上升态势。半变动成本指总额的开始值一定,然后随着产量的变化作相应变动的有关成本。按照一定的方法把混合成本分解为变动成本和固定成本,称为混合成本的分解。半固定成本这类成本是在一定业务量范围内其成本保持不变,相当于固定成本,当业务量突破这一范围,成本就会跳跃上升,在一定时期又不变。半变动成本这类成本通常有个初始的量,一般不变,相当于固定成本,在这个基础上,随着业务量的变动而变动的成本。
(2)销售收入、产品成本和产品产量的关系。线形盈亏平衡分析法中的线形关系指的是销售收入与销售量之间、产品成本与产品产量之间的关系是线形的。
在无竞争市场中,生产销售活动不会明显地影响市场供求状况,市场的其他条件也不变,产品价格不随销售量的增加而变化,可以看作为一个常数,销售收入与销售量之间为线形关系:
![]()
式中 B——总销售收入;
P——单位产品价格;
Q——产品销售量。
(3)产品成本与产品产量的关系。产品总成本是固定成本和变动成本之和,它与产品产量之间的关系可以近似地认为是线形关系,即
![]()
式中 C——产品总成本;
Cf——固定成本;
Cv——单位产品变动成本。
(4)确定盈亏平衡点(BEP)。因为盈亏平衡点是盈利与亏损的分界点,已知总销售收入和产品总成本相等时,可以求出一临界点,即盈亏平衡点,所以我们也将盈亏平衡法称为临界分析法。
如图6-1所示,图中横坐标表示产品产量,纵坐标表示总销售收入B或产品中成本C,线形平衡点为销售收入与产品销售量呈线形关系时所对应的盈亏平衡点,直线OB代表公式B=PQ,直线Cf C代表直线C=Cf+CvQ。两条直线的交点为BEP。设盈利E=B-C,通过E的大小可以确定方案是否盈利。在交点左边的空白区域,E小于0,产品总成本总大于总销售收入,方案亏损;在交点右边阴影区域,E大于0,产品的总成本总小于总销售收入,方案盈利;在BEP点上,销售收入等于产品总成本,方案不盈不亏。相对于这个点,运用解析法进行计算
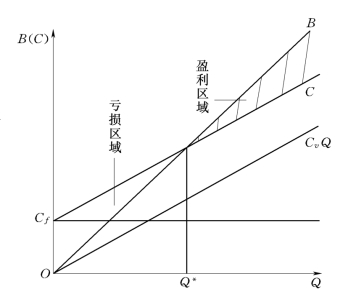
图6-1 销售收入与产品销售量线形关系图
B=C
即
![]()
则
![]()
由式(6-4)可以看出,P-Cv是总成本减去了变动成本后的净成本,称为边际贡献。下面运用上述公式进行实际意义的讨论。
在产品销售价格、固定成本、变动成本不变的情况下,盈亏平衡销售收入为
![]()
设方案设计生产能力为Qd,在产品销售价格、固定成本、变动成本不变的情况下,盈亏平衡生产能力利用率为
![]()
若按设计生产能力进行生产和销售,且产品固定成本、变动成本不变,则盈亏平衡销售价格为
![]()
若按设计生产能力进行生产和销售,且产品固定成本、销售成本不变,则盈亏平衡单位产品变动成本为
![]()
【例6-1】重庆宗申公司的某工程设计生产能力为10000辆摩托车,每辆车售价为5000元,而其固定成本为1200000元,单位变动成本为2600元/辆,请进行盈亏平衡分析。
解:由式(6-4)求临界平衡点:
![]()
由式(6-5)求盈亏平衡销售收入:
B*=PQ*=5000×5000=25000000(元)
由式(6-6)求盈亏平衡生产能力利用率:
![]()
2.非线性盈亏平衡分析法
非线性盈亏平衡分析法中销售收入与销售量之间、产品成本与产品产量之间的关系是非线性的。在市场上,根据不同的条件,非线性关系可以用二次函数、三次函数来表示,我们用以产品Q为自变量的函数f(Q)来表示总销售收入,以产品Q为自变量的函数g(Q)来表示总成本。
这里设定销售收入是产量的非线性函数:
![]()
设定总成本是产量的非线性函数:
![]()
运用解析法进行计算:
![]()
求盈亏平衡点,即
![]()
求解式(6-12)从而求出Q*。解此二次方程,得到几个解,可以通过实际条件从而确定盈亏平衡点。另外,与线性盈亏平衡分析法不同的是,可以通过对P(Q)求导并且结果为0,求得最大盈利点,即
![]()
如图6-2所示,由于销售收入是曲线分布,所以可能产生两个或两个以上的盈亏平衡点BEP1与BEP2,在它们之间的阴影部分,总销售收入总大于产品总成本,在这个区域内,方案总是盈利;在两个盈亏平衡点以外的部分区域,总销售收入总大于产品总成本,方案总是亏损。
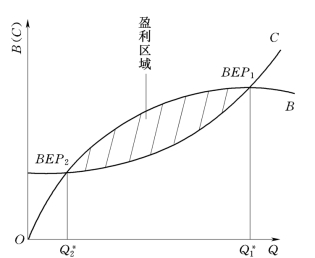
图6-2 销售收入与产品销售量非线形关系图
【例6-2】重庆103制药厂生产一批药品,总成本C、产品销售收入B与产品销售量Q有关,关系式为B=2Q 2-4Q和C=Q2-Q-2,其总固定成本为1000000元,单位变动成本为20元/盒,试确定该药品最优销售量。
解:药品销售收入
B=f(Q)=2Q2-4000Q
药品总成本
C=g(Q)=Q 2-1000Q-2000000
根据盈亏平衡点处
P(Q)=f(Q)-g(Q)=Q2-3000Q+2000000=0
求解上式得盈亏平衡点为
Q=1000或2000(盒)
由式(6-13)
![]()
求解得该药品最优销售量为
Q=1500(盒)
(三)多方案盈亏平衡分析
与单方案盈亏平衡分析不同,多方案盈亏平衡分析是对多个方案进行研究,这里的多个方案的经济效益指标值受某不确定因素x的影响,建立各方案经济效果指标与不确定因素之间的函数关系(见图6-3)。由于各方案经济效果函数的斜率不同,所以各函数曲线必然会发生交叉,即在不确定因素的不同取值区间内,各方案的经济效果指标高低的排序不同,由此来确定方案的取舍。这样的方法也称为优劣平衡分析方法。即
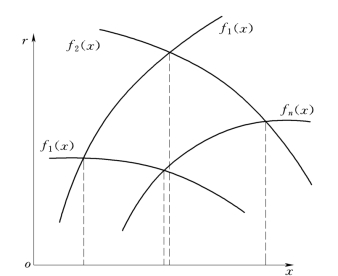
图6-3 各方案经济效果指标与不确定因素之间的函数关系图
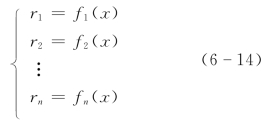
在两个方案的经济效益相等时,即
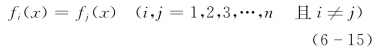
式中 ri——第i个方案的指标值(因变量);
x——不确定因素(自变量);
fi(x)——第i个方案的指标值随着自变量x变化的函数关系。
解出使等式成立的x值,即为两方案的盈亏平衡点,可以以此决定方案的优劣,从而进行选择。
【例6-3】假设某工厂拟建几栋仓库,初步拟定A、B、C三种结构设计方案。三种方案的费用见表6-1。试分析在不同的建筑面积范围内采用哪个方案最经济(ic=10%)。
表6-1 三种结构设计方案的费用表

解:设仓库的建筑面积为xm2,则

如图6-4所示,三种方案的费用现值PC与建筑面积x之间成函数关系,利用盈亏平衡分析法,求出三种方案的优劣平衡分歧点:xAB=525m2,xBC=629m2,xAC=583m2。通过进一步绘制多方案盈亏平衡分析图,可以得出以下的分析结论:当仓库的建筑面积小于583m2时,选择C方案;当仓库的建筑面积大于583m2时,选择A方案;B方案在任何情况下都是不经济的。
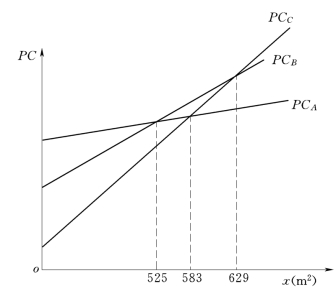
图6-4 费用现值PC与建筑面积x之间的函数关系
二、敏感性分析
(一)概述
1.定义
敏感性分析也称为灵敏度分析,是评价和管理决策中常用的一种不确定性分析方法,它在假设其他因素不变的前提下分析某个或某几个因素变动幅度对目标的影响程度,以判定因素的变化对目标影响的重要性。
2.目的和作用
敏感性分析可以研究经济效果指标变动的范围,从而找出影响工程的经济效果的最关键因素,即最敏感因素,然后通过多方案敏感性大小的对比,选取敏感性小的方案,分析可能出现的最有利与最不利的经济效果范围,寻找可以替代的方案或是对原方案采取某些控制措施,并用来确定最现实的方案。
3.影响方案的因素
从实际情况上来分析,影响方案的因素很多,有大有小,有主有次,总结各方面的经验,对一般的投资作敏感性分析的因素通常从下列因素中选定:
(1)投资额。包括固定资产投资与流动资金占用,根据需要还可将固定资产投资划分为设备费用、建筑安装费用等。
(2)建设期限、投产期限。
(3)产品产量及销售量。
(4)产品价格。
(5)经营成本。特别是其中的变动成本。
(6)寿命期。
4.分析步骤
进行敏感性分析可以分为以下几个步骤:
(1)确定具体的要进行敏感性分析的经济评价指标(分析指标)。这些评价指标必须是根据投资的特点和实际需要来确定,一般选择最能反映经济效益的综合性评价指标作为分析或评价的对象。如净现值、净年值、内部收益率、投资回收年限等都可能作为敏感性分析的指标。由于敏感性分析是在确定性分析的基础上进行的,一般不能超出确定性分析所用的指标范围另立指标。当确定性经济分析中使用的指标较多时,敏感性分析可能围绕其中1(或若干)个最重要的指标进行。
(2)选择不确定因素。首先可以预计这些不确定因素在可能的变化范围内,对投资效果影响较大;或者是这些不确定因素发生变化的可能较大,比如总投资、经营成本等。投资额、建设工期、产品价格、生产成本、贷款利率、销售量等均可能是影响方案经济效果的不确定因素,这些因素中的任何一个发生变化都会引起方案经济效果的变动。敏感性分析,并不是要把出现在实际工作中的所有的不确定因素都纳入考虑范畴,而应该根据方案特点的实际情况,选择对方案经济效果影响较大的因素进行不确定性分析。
(3)确定不确定性因素的变动范围。应该根据实际情况,确定各个不确定因素的变动范围,设定不确定因素的变化范围。
(4)计算各个不确定因素对经济评价指标的影响程度。确定范围后,可进行影响程度的计算。首先应在固定其他因素的前提下,变动其中1个(或多个)不确定因素,并根据变化范围改变其他的数值,通过已知数值计算这种变化对经济评价指标的影响数值,最后将其与该指标的原始数值相比较,得出该指标的变化率。用公式表示如下:
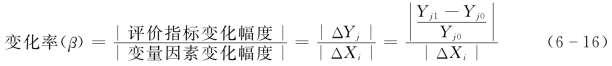
式中 β——变化率,又称灵敏度;
ΔXi——第i个不确定因素(变量因素)的变化幅度;
ΔYj——第j个指标受不确定因素(变量因素)变化影响的差额幅度;
Yj0——第j个指标受变量因素变化影响后所达到的指标值;
Yj1——第j个指标未受变量因素变化影响时的指标值。
(5)寻找敏感因素。敏感因素是指对经济评价指标产生较大影响的因素,根据分析问题的目的不同一般可通过两种方法来确定。一种称为相对测定法,另一种称为绝对测定法。相对测定法,即假定需分析的因素均从基准值开始变动,各种因素每次变动幅度相同,比较每次变动对经济指标的影响效果。绝对测定法,即假定要分析的因素均向只对经济评价指标产生不利影响的方向变动,并设该因素可能达到悲观值(最坏值),然后计算在此条件下的经济评价指标,如果计算出的经济评价指标已超过了可行的临界值,从而改变了方案的可行性,则就表明该因素是敏感因素。
(6)综合评价,优选方案。根据分析结果,综合评价各方案,优选最优方案。
(二)敏感性分析方法的种类
影响方案选择的因素有很多,有主要因素,有次要因素,根据考虑的不确定性因素的数量,可以将敏感性分析分为单因素敏感性分析和多因素敏感性分析。单因素敏感性分析适合于分析方案的最敏感因素,但是在实际中,各个因素的变化都是有联系的,一个因素变化往往会使其他因素产生变化;多因素敏感性分析同时考虑了很多因素,敏感性分析要考虑可能发生的各种因素不同变动幅度的多种组合,计算起来要比单因素敏感性分析复杂得多。
1.单因素敏感性分析
单因素敏感性分析是指每次只变动一个因素,而其他因素保持不变时所进行的敏感性分析,也就是就单个因素的变动对方案经济效果影响所作的分析。它可以表示为该因素按一定百分率变化时所得到的评价指标值,也可表示为评价指标达到临界点时,某一因素变化的极限变化率或弹性容量。
以下通过举例来说明单因素敏感性分析在实际中的应用。
【例6-4】重庆华磊混凝土公司计划投资新建先进的混凝土生产线,该基本方案的参数估算值如表6-2所示,试分别就固定资产投资、营业现金流量、固定资产残值进行敏感性分析(已知基准折现率为ic=10%)。
表6-2 投资使用年限内的各年现金流量 单位:元

解:选择净现值(NPV)为敏感分析对象,每年的现金流量图如图6-5所示。
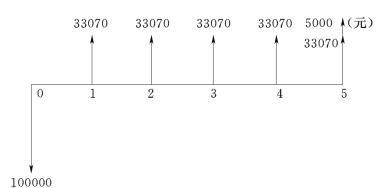
图6-5 现金流量图
计算出在初始条件下的净现值:

现讨论期初投资、营业现金流量、期末残值、使用年限及基准折现率的变化对净现值的影响(假设各因素最大可能变化幅度为30%),此时,固定资产投资变化率为X;营业现金流量变化率为B;期末残值变化率为C;使用年限变化率为D;基准折现率变化率为E。
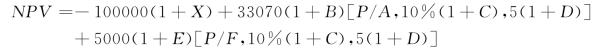
由表6-3和表6-4看出,对净现值影响最大的因素是年营业现金流量,其次是固定资产投资和使用年限,再次是基准折现率,而残值为不敏感因素。其中:(+)代表使用年限增加,(-)代表使用年限减少。
表6-3 各因素变化对净现值的影响 单位:元
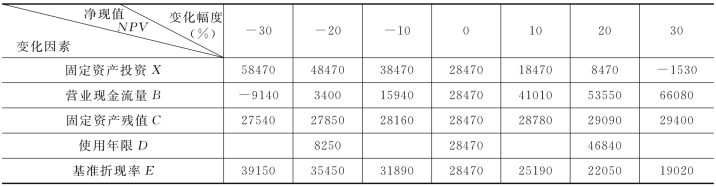
表6-4 各因素每变化1%引起的净现值变化

注 (+)代表使用年限增加,(-)代表使用年限减少。
通过计算,由图6-6,固定资产投资变化幅度超过28.47%时,净现值由正变为负,由可行变为不可行;营业现金流量变化幅度超过-22.71%时,净现值由正变为负,由可行变为不可行;固定资产残值变化幅度超过-918.39%时,净现值由正变为负,由可行变为不可行;使用年限变化幅度超过-28.16%时,净现值由正变为负,由可行变为不可行;基准折现率变化幅度超过90.38%时,净现值由正变为负,由可行变为不可行。进行项目因素控制时,优先选用对项目影响较大的因素。
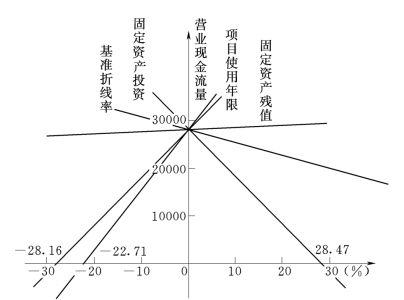
图6-6 敏感性分析图(单位:元)
2.多因素敏感性分析
单因素敏感性分析是指每次只变动一个因素,而其他因素保持不变,但是在实际工程中,独立不变的因素并不存在,不同的因素之间有一定的联系,某一因素的变化可能引起其他的因素的相关变化。与单因素敏感性分析不同,多因素敏感性分析则考虑了这种相关性,因而能反映多因素变动对经济效果产生的综合影响,弥补了单因素敏感性分析的缺欠,更全面地揭示事物的实质。因此,多因素敏感性分析要考虑各种因素可能发生的不同变动幅度的多种组合,分析其对方案经济评价指标的影响程度。因此,在对一些有特殊要求的方案进行敏感性分析时,除了进行单因素敏感性分析外,还应进行多因素敏感性分析。以下进行举例讨论。
【例6-5】根据[例6-4]的数据,对固定资产投资和营业现金流量的变动进行多因素敏感性分析。
解:沿用[例6-4]的数据,只考虑固定资产投资和营业现金流量的变动,则方案的净现值计算公式为
NPV=-100000(1+X)+33070(1+B)(P/A,10%,5)+5000(P/F,10%,5)
经过整理得
NPV=28466-100000X+33070B
当NPV=0时,则有
100000X-33070B=28466
由上式,在直角坐标系中画出NPV=0临界线,如图6-7所示,X轴表示固定资产投资变动的百分率,B表示营业现金流量变动的百分率,即为一条NPV=0的临界线。在临界线上,NPV=0在临界线左上方的区域,NPV>0;在临界线右下方的区域,NPV<0。当固定资产投资和营业现金流量同时变动的范围在临界线左上方时,则表示方案是可以接受的。
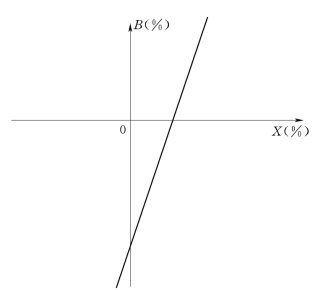
图6-7 敏感性分析图
(三)敏感性分析的局限性
多因素敏感性分析结合实际情况,考虑了影响方案的多个不确定因素,并且进行综合计算,但是多因素敏感性分析忽略了各个不确定因素的发生概率对方案经济效果的影响。对于一些不确定因素,虽然它的发生会对方案经济效果产生很大的影响,但是如果发生的概率很小,甚至可以忽略不计,则影响效果就可以忽略。可是另外存在一些不确定因素,他们对方案经济效果影响小,如果其发生的概率很大,则将会对方案经济效果产生很大的影响。所以,敏感性分析也存在一些局限性,下面介绍另外一种方法——概率分析来解决这个问题。
三、概率分析
(一)概述
1.概率分析的定义
概率分析又叫风险分析,是根据不确定性因素变动的概率分布,分析对经济效益的影响,从而对风险情况作出比较准确分析的一种定量分析方法。该分析方法应用在给定方案所产生结果的不确定情况下,方案的实施可能有多个结果,最多我们可以知道效益或费用发生的概率。而在最不利的情况下,可以得到效益或费用发生的范围,但却不可能知道其发生的概率。
2.概率分析的基本原理
盈亏平衡分析和敏感性分析是不确定性分析常用的两种方法,但这两种方法都隐含了一个假设,即各个不确定性因素发生变动的可能性相同。事实上,各个不确定性因素在未来发生某一幅度变动的概率是不尽相同的,这就提出了概率分析的要求。在评价中,根据方案特点和实际需要,有条件时还应进行概率分析。与盈亏平衡分析和敏感性平衡分析不同,概率分析与概率统计学有很大的联系,如果影响方案经济效果的各种不确定性因素多服从某种分布(如平均分布、正态分布等),那么以这些不确定性因素为参数的经济评价指标应该是随机变量。在进行概率分析时,先对各个不确定性因素作出概率估计,并以此为基础计算方案的经济评价指标,最后求出经济评价指标的期望值、累计概率、标准差及离差系数等来表示方案的不确定性。
3.概率分析的步骤
根据概率分析的基本原理,概率分析可以按照以下步骤进行:首先选定工程效益指标作为与分析对象有关的不确定性因素,如投资、经营成本、销售价格等;然后估计出每个不确定因素的变化范围及其可能出现的概率;然后在不确定性因素变量的影响下计算方案经济效益的期望值;然后计算出表明期望值稳定性的标准差或变异系数;最后综合考虑期望值和标准偏差,说明在该不确定因素情况下方案经济效益指标的期望值以及获取此效益的可能性。
(二)概率分析的计算
1.概率分布
结合概率统计学知识对概率分析进行讨论,随机变量的概率分布可以分为离散型概率分布和连续型概率分布。以下对于两种概率分布进行简要的介绍。
(1)离散型概率分布。随机变量可分为离散型随机变量和连续型随机变量。离散型随机变量是指事件发生的可能性变化为有限次数,并且每次发生的概率值为确定值的变量。离散型概率分布包括两点分布、两项分布、退化分布、几何分布、泊松分布等。必须熟练掌握这些分布的期望值、标准差与差异系数等指标。
(2)连续型概率分布。许多经济分析的随机现象可以近似地用满足某种连续型随机变量来描述,概率统计学中连续型概率分布包括均匀分布、正态分布、卡方分布、Γ分布、β分布、F—分布、t—分布等,这里用均匀分布和正态分布为例进行分析。
1)均匀分布。概率分布为
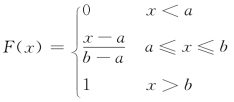
其密度函数为p(x),F(x)是一个连续型分布,相应的随机变量可能的取值区间为[a,b](见图6-8)。
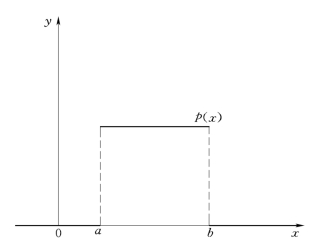
图6-8 均匀分布图
2)正态分布。设随机变量x满足正态分布,如图6-9所示,其相应的密度函数是
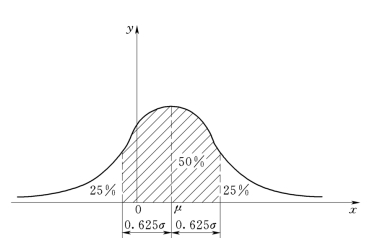
图6-9 正态分布图

令u=![]() ,代入式(6-17),可得
,代入式(6-17),可得
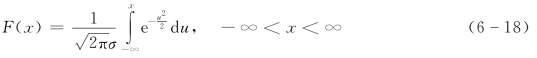
可以看出经过变换后,随机变量服从标准正态分布。如图6-9所示,原来的y轴移动到了x=μ上,在直线y=μ左右各0.625σ的阴影范围内,概率为50%。当离x=μ直线距离不同时,中间阴影所表示的范围也不一样。
![]()
式中 σ——方差。
(3)计算期望值、标准差与差异系数。求随机变量的期望值、标准差与差异系数,以之作为评价方案经济效益的标准,以下通过统计概率学进行计算。
对于离散型随机变量
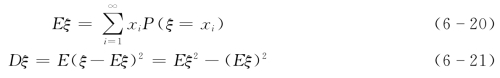
对于连续型随机变量
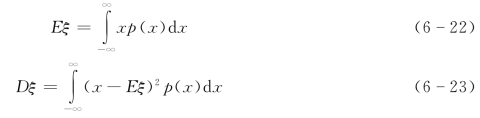
差异系数
![]()
期望值、标准差与差异系数为:
1)均匀分布
![]()
2)正态分布
![]()
(4)净现值的期望值、标准差和变异系数。在实际情况中,大部分的概率分析都是以净现值的数字特征参数的计算为基础的,作为随机变量,期望值和标准差是描述净现值数字特征的主要参数。
期望值、标准差和变异系数是用来描述随机变量的几个主要参数,期望值是反映随机变量取值的平均值,但平均值绝不是一般意义上的算术平均值,而是以随机变量各种取值的概率为权重的加权平均值;标准差是用来度量随机变量与其均值(期望值)偏离程度的参数;为了比较期望值不同的投资之间的风险程度大小,需要引进“变异系数”的概念。变异系数是标准差除以期望值的商。
净现值的期望值为
![]()
式中 E(NPV)——NPV的期望值;
NPVi——各种现金流量下的净现值;
Pi——对应于各种现金流量的概率值。
净现值的标准差为
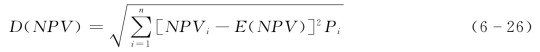
式中 D(NPV)——净现值的标准差。
变异系数
![]()
以净现值指标的分析为例,设某方案的寿命期为n年,在各种不确定因素综合影响下,该方案的净现金流量序列呈k种状态。于是在第I种状态下,方案的净现值为
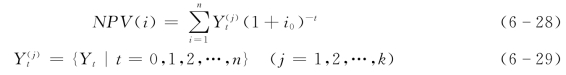
式中 Yt——第t年的净现金流量;
k——自然数,其值为各个输入变量能取值的个数的连乘积。
2.计算方法
概率分析有以下几种常用方法:
(1)期望值法。期望值法是通过计算计算期内不确定因素的发生概率和经济评价指标的期望值,来判断风险程度的一种方法。
【例6-6】计划修建李家沱长江大桥来改善城市的交通状况,其中有4套方案可采纳,分别是甲、乙、丙、丁4个方案,按照每个方案修建好大桥后考虑其每年的经济效果(收入),经济效果分为A(好)、B(比较好)、C(一般)、D(亏损)、E(严重亏损),试进行方案选择(所有的数据如表6-5所示)。
表6-5 大桥修建方案资料数据表 单位:万元
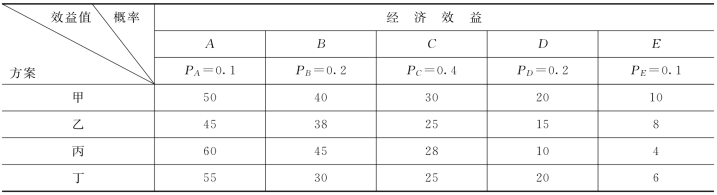
解:如表6-5数据进行计算并依据它来判断,对于每个方案求期望值。
对于甲方案:
E(X)A=50×0.1+40×0.2+30×0.4+20×0.2+10×0.1=30.0(万元)
对于乙方案:
E(X)B=45×0.1+38×0.2+25×0.4+15×0.2+8×0.1=25.9(万元)
对于丙方案:
E(X)C=60×0.1+45×0.2+28×0.4+10×0.2+4×0.1=28.6(万元)
对于丁方案:
E(X)D=55×0.1+30×0.2+25×0.4+20×0.2+6×0.1=26.1(万元)
可以看出,甲方案的期望值最高,是最优方案,因此选择甲方案。
【例6-7】为加强宜宾市在长江沿岸的货运能力,加强长江两岸的交通能力,计划兴建一个新码头,寿命期为20年,这里有4个方案可以进行选择,可能出现的数值及相应的概率如表6-6所示,如果ic=10%,试计算净现值(NPV)的期望值,试进行方案的选择。
表6-6 码头修建方案资料数据表
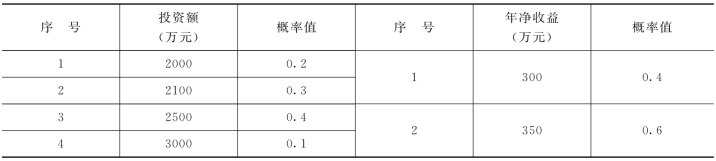
解:根据表6-6,投资额和年净收益之间可以有8种组合,每种组合都有不同的净现值。
先计算一种组合:
投资额 A1=4500(万元)
年净收益 B1=300(万元)
组合概率 p1=0.2×0.4=0.08
净现值 NPV1=-2000+300(P/A,10%,20)=554.1(万元)
根据以上的计算方法,计算其余的组合,从而得出表6-7。
表6-7 净现值计算表
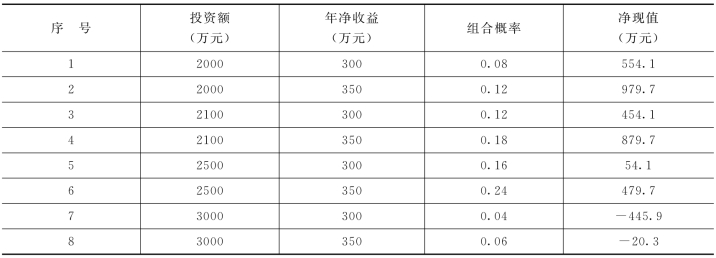
计算期望值:
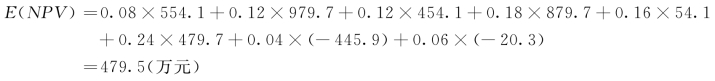
P(NPV>0)=1-0.04-0.06=0.9
可以看出,净现值的期望大于0,表明方案可以接受;并且净现值大于0的概率为0.9,表明方案有较大的抗风险能力。
(2)决策树法。决策树法如第七章所述。
(3)蒙特卡罗法。蒙特卡罗法是一种随机模拟方法,它是利用随机数或某种概率现象模拟现实问题,该方法可以对现实问题进行分析和作出预测。对随机变量的数值模拟相当于一种“试验”,所以蒙特卡罗法又称为统计试验法。由于蒙特卡罗方法比较简单,能够保证结果依概率收敛,所以适合用于可靠度的计算。
蒙特卡罗模拟法的实施步骤一般为:①通过敏感性分析,确定风险随机变量;②确定风险随机变量的概率分布;③通过随机数表或计算机求出随机数,根据风险随机变量的概率分布模拟输入变量;④选取经济评价指标,如净现值、内部收益率等;⑤根据基础数据计算评价指标值;⑥整理模拟结果所得评价指标的期望值、方差、标准差和它的概率分布及累积概率,绘制累计概率图,计算可行或不可行的概率。
