简单综合评价方法
在介绍一些常见简单的综合评价方法前，必须进行综合评价的准备工作，确定进行综合评价的数学模型，建立评价指标并进行筛选，对评价指标进行无量纲化，之后确定各评价指标的权重系数。以下便依次进行介绍。
一、综合评价的数学模型
这里，我们讨论得最多的是多指标（或多属性）综合评价。它需要一个整体性的综合评价值进行评价，综合评价值是通过一定的数学模型（或算法）由多个评价指标值合成的。可用于合成的数学方法较多，问题在于我们如何根据评价目的（或准则）及被评价系统的特点来选择较为合适的合成方法。即在评价n个系统（即被评价对象）的运行（或发展）状况，在已获得n个状态向量xi=（xi1，xi2，…，xim）T（i=1，2，…，n）的基础上，构造系统状态在某种意义下的综合评价函数。也就是说，在获得n个系统的评价指标值
的基础上，如何选用或构造综合评价函数
式中 w=（w1，w2，…，wm）T——指标权重向量；
x=（x1，x2，…，xm）T——系统的状态向量。
（一）线性加权综合法
1．计算公式
式中 y——系统（或被评价对象）的综合评价值；
wj——与评价指标相应的权重系数（0≤wj≤1，j=1，2，…，m）。
式（10-5）是一线性模型，运用此式进行综合评价的方法就是线性加权综合法。
权重系数满足
2．线性加权综合法的特性
通过实际情况事例，线性加权综合法具有以下的一些特征。线性加权综合法适用于各评价指标间相互独立的场合，此时各评价指标对综合评价水平的贡献彼此是没有什么影响的。出于合成运算采用的方式，其现实关系应是各部分之和等于总体，若各评价指标间不独立，和的结果必然是信息的重复，也就难以反映客观实际，可使各评价指标问题得以线性地补偿。即某些指标值的下降，可以由另一些指标值的上升来补偿，任一指标值的增加都会导致综合评价值的上升。任一指标值的减少都可用另一些指标值的相应增量来维持综合评价水平的不变。线性加权综合法中权重系数的作用比在其他“合成”法令更明显些，突出了指标值或指标权重较大者的作用；当权重系数预先给定时（由于各指标值之间可以线性地补偿）对区分各备选方案之间的差异不敏感，线性加权综合法对于（无量纲的）指标数据没有什么特定的要求，并且容易计算、便于推广普及。
（二）非线性加权综合法
1．计算公式
用非线性模型来进行综合评价的方法称为非线性加权综合法，公式为
2．非线性加权综合法的特性
通过实际情况事例，非线性加权综合法具有以下的一些特征：加法评分法相对于乘法评分法适用于各指标间有较强关联的场合；它强调的是各备选方案（无量纲）指标值大小的一致性，即这种方法是突出评价指标值中较小者的作用，这是由乘积运算的性质所决定的；指标权重系数的作用不如线性加权综合法那样明显；对指标值变动的反映比线性加权综合法更敏感。因此，非线性加权综合法更有助于体现备选方案之间的差异；对指标值的数据要求较高，即要求无量纲指标值均不小于1；与线性加权综合法相比，非线性加权综合法在计算上要复杂些。
（三）增益型线性加权综合法
1．增益函数
对取定的s（s＞0，且s≠1），称映射
μ∶[0，1]→[0，s]
为一个增益函数，如果它满足：
（1）μ连续，分段可导；
（2）若x1≥x2，则μ（x1）≥μ（x2），μ′（x1）≥μ′（x2）；
（3）μ（0）=0，μ（1）=s，μ（0．5）＜0．5。
则当s＞1时，μ为增益；当0＜s＜1时，μ为折损。
2．构造综合评价函数
前边已得出增益函数，将增益函数运用于综合评价上，得出综合评价函数
（四）理想点法
对于一个综合评价问题，评价的目标明确，先设定一个理想的系统或样本点（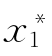
，
，…，
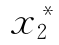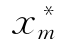），被评价对象为（xi1，xi2，…，xim），如果在某种变换计算或某种意义下非常接近，被评价对象与理想系统之间有一定的“距离”，如果这个距离非常小，则称被评价对象为（xi1，xi2，…，xim），是最优的。基于这种思想所得出的综合评价方法，称为逼近样本点或理想点的排序方法，简称为理想点法。
定义
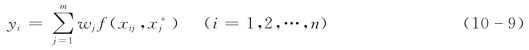
为被评价对象与理想系统之间的“距离”。
式中 f（xij，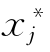
）——分量xij与
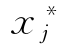之间的“距离”。
举例：当
时，有
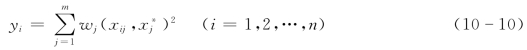
式中 yi——欧氏（加权）距离。
当yi=0时，si即达到或成为理想点s*。这时，可以按yi值的大小对各被评价对象进行排序。
二、综合评价指标
各个系统的运行（或发展）状况可用一个向量x表示，其中每一个分量都从某一个侧面反映系统在某时段（或时刻）的发展状况，故称x为系统的状态向量，它构成了评价系统的指标体系。同时，评价指标的选择也要注意，指标是不是选取得越多就越全面呢？太多了，事实上是重复性的指标，会有干扰；太少了，可能所选的指标缺乏足够的代表性，会产生片面性。每一项指标都是从一个方面反映了评价对象的某些信息，如何正确地、科学地使用这种信息，就是综合评价要处理的问题。
（一）选择评价指标的原则
正是因为要正确地科学地选择评价指标，因此在选择的时候需要遵守一定的原则，这里列举出一些常用的原则，以供解决实际问题时参考。
1．目标明确
在考虑一座桥梁耐久性的时候，应选择与耐久性有关的指标：混凝土性能、混凝土养护条件、施工质量、施工环境等。可以看出所选用的指标目的很明确，从评价的内容来看，该指标确实能反映有关的内容，反映多与少是另一类问题，决不能将与评价对象、评价内容无关的指标也选择进来。
2．比较全面
在进行综合评价的同时，影响评价对象的因素有很多，特别是在实际环境中，很多因素可能是预测不到的，如果遗漏一些因素，可能对综合评价产生一定的影响，所以评价只要求比较全面地考虑影响因素的问题。比较全面的另一种说法就是有代表性，所选的指标确能反映要评价的内容，虽然不是全部，但代表了某一侧面。
3．切实可行
用通俗一些的说法，就是可操作性。有些指标虽然很合适，但无法得到，就不切实可行，缺乏可操作性。综合评价在一定意义下就是凭借一些可以直接观察、测量的指标去推断不可观察、测量的性能。
（二）评价指标筛选方法
在按一些原则确定指标体系后，这些量都是可以观察、测量的。在这个基础上，就可以用统计分析中的一些方法来选出一部分，它们有很好的代表性，使得在综合评价时，工作就更容易些。筛选方法有很多，这里我们只介绍其中比较简单的两种。
1．专家调研法
这是一种向专家发函、征求意见的调研方法。评价者可根据评价目标及评价对象的特征，在所设计的调查表中列出一系列的评价指标，分别征询专家对所设计的评价指标的意见，然后进行统计处理，并反馈咨询结果，经几轮咨询后，如果专家意见趋于集中，则由最后一次咨询确定出具体的评价指标体系。
2．极大不相关法
从统计分析的眼光来看，给定p个指标x1，…，xp的n组观察数据，就称为给了n个样本，相应的全部数据用矩阵X表示，即
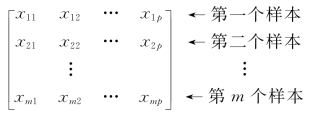
第一行代表一个样本的观察值，X是n×p的矩阵，利用X的数据，可以算出变量xi的均值、方差与xi、xj之间的协方差。
如果与其他的指标是独立的，那就表明是无法由其他指标来代替的，因此保留的指标应该是相关性越小越好，在这个想法下，就导出极大不相关方法。首先求（样本的）相关阵R。
式中 rij——xi与xj的相关系数，它反映了xi与xj的线性相关程度。
现在要考虑的是一个变量xi与余下的p-1个变量之间的线性相关程度，称为复相关系数。通常记为
这个符号太复杂，现在简化为ρi，但要注意它的意义。ρi可以由下面的公式来计算。先将R分块，例如要计算ρp，就将R写成
（注意R中的主对角元素rit=1，i=1，2，…，p），于是
类似地，要计算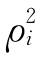
时，将R中的第i行、第i列经过置换，放在矩阵的最后一行，最后一列，此时：
于是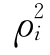
的计算公式为
算得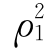
，…，
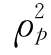后，其中值最大的一个，表示它与其余变量相关性最大，指定临界值D之后，当
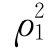＞D时，就可以删去x1。
三、评价指标无量纲化
无量纲化，也称为指标数据的标准化、规范化。如果我们把指标无量纲化以后的数值称为指标评价值，那么无量纲化过程就是指标实际值转化为指标评价值的过程，无量纲化方法也就是指如何实现这种转化。从数学角度讲，就是要确定指标评价值依赖于指标实际值的一种函数关系式。我们把无量纲化方法从几何的角度归结为三类：直线型无量纲化方法、折线型无量纲化方法、曲线型无量纲化方法。
（一）直线型无量纲化方法
直线型无量纲化方法在将指标实际值转化成不受量纲影响的指标评价值时，假定两者之间呈线性关系，指标数实际值的变化引起指标评价值一个相应的比例变化。常用的直线型无量纲化方法有以下几种：阈值法、标准化法、比重法等。
1．阈值法
阈值是衡量事物发展变化的一些特殊指标值，比如极大值、极小值、满意值、不允许值等。阈值法是将指标实际值xi与该种指标的某个阈值相对比，从而使指标实际值转化成评价值的方法。其无量纲化公式主要有
特点：评价值yi随指标值增大，若指标值均为正，则评价值不可能为0，指标最大值的评价值为1。
特点：评价值随指标值增大而减小，适合于无量纲化和指标转化同时进行。
特点：评价值随指标值增大而减小，适合于无量纲化和指标转化同时进行。
特点：评价值随指标值增大而增大，指标最小值的评价值为0，指标最大值的评价值为1。
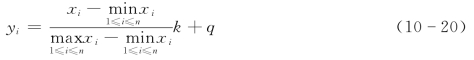
特点：评价值随指标值增大而增大，指标最小值的评价值为q，指标最大值的评价值为k+q。
实际在多数情况下，所有的指标值均大于0，故以上按所有xi＞0处理，事实上若有部分xi≤0，公式仍然适用。最后两个公式实质是一样的，只不过评价值的范围有所变化。我们可以用同样的方法将前几个公式的评价值范围变到希望的范围内。在弄清这些公式的特点之后，就可以灵活选用或构造新的公式。
2．标准化法
标准化法可将多组不同量纲的数据标准化后进行比较，在综合评价中需要借助标准化法来消除数据量纲的影响，标准化公式如下：
式中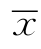
——数据均值；
s——数据标准差。
指标实际值与评价值的关系如图10-3所示：x坐标代表指标实际值；y坐标代表评价值；直线与x轴相交，交点是数据均值点。
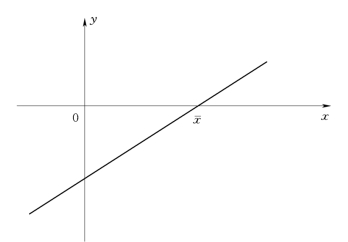
图10-3 指标实际值与评价值的关系图
3．比重法
比重法无量纲化公式主要有
式（10-22）适合指标值均为正数的情况，且评价值之和满足
式（10-23）适合于指标值有负值的情况，一般情况下，指标评价值不满足式（10-24）而是满足
（二）折线型无量纲化方法
有时，指标在不同区间内的变化，对被评价事物的综合水平影响是不一样的。比如xi小于某个点xm时，xi变化对综合水平影响较大，此时评价值yi也应有较大的变化；当xi大于xm时，xi变化对被评价事物综合水平影响较小，则yi也应变化较小。在上述情况或者其相反的情况下，应采用折线型的无量纲化方法来分段处理。
1．二折线型
如果采用极值化方法分段作无量纲处理，有公式如下
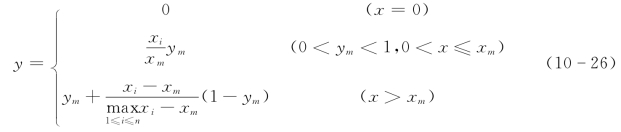
通过式（10-26），可以画出指标评价值y和指标实际值x之间的关系，如图10-4所示。
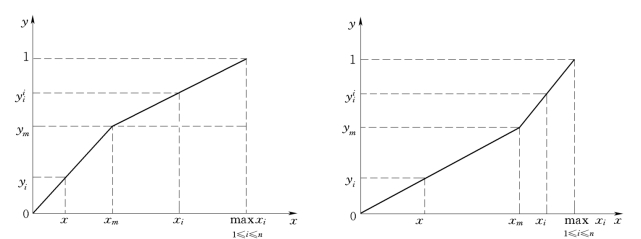
图10-4 指标实际值与评价值的关系图
2．三折线型
对于三折线型，有公式如下
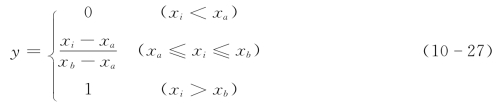
通过式（10-27），可以画出指标评价值y和指标实际值x之间的关系，如图10-5所示。
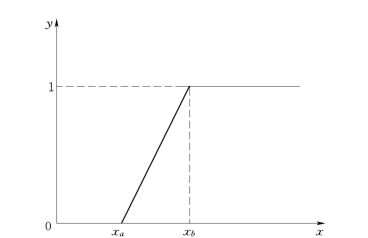
图10-5 三折线型指标实际值与评价值的关系图
（三）曲线型无量纲化方法
指标值xi与评价值yi之间的关系可以是前边的直线或是折线关系，但是在实际当中，很多情况下，指标实际值对评价值的影响不是等比例的，而是非线性关系，这就可以采用曲线型无量纲方法。曲线型无量纲化方法有很多种，下边是介绍升半Г型分布、半正态型分布、升半哥西分布、升半凹（凸）分布和升半岭型分布（见图10-6）。
1．升半Г型分布
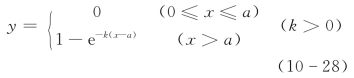
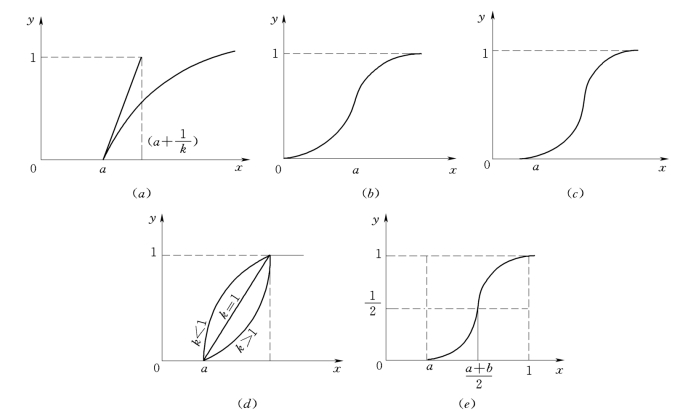
图10-6 曲线型指标实际值与评价值的关系
（a）升半Г型分布；（b）半正态型分布；（c）升半哥西分布；（d）升半凹（凸）分布；（e）升半岭型分布
2．半正态型分布
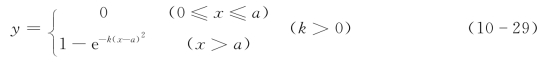
3．升半哥西分布
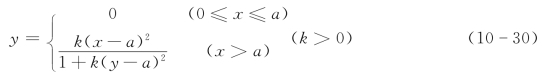
4．升半凹（凸）分布
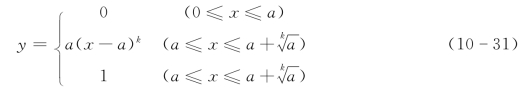
5．升半岭型分布
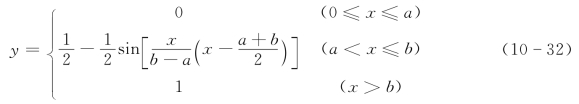
四、权重系数
对实际问题选定被综合的指标后，确定各指标的权的值，一些方法都是利用专家或个人的知识或经验得来的，所以称为主观赋权法，但这些专家的判断本身也是从长期实际中来的，不是随意设想的，应该说有客观的基础；另一些方法是从指标的统计性质来考虑，它是由调查所得的数据决定，不需征求专家们的意见，所以有的书上称为客观赋权方法。另外，权重系数的确定方法也可以分为直接评分法和间接评分法，如图10-7所示。
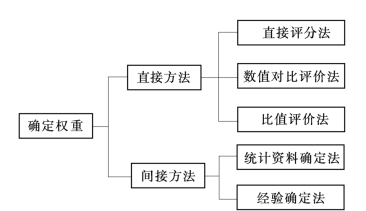
图10-7 权重确定方法
相对于某种评价目标来说，评价指标之间的相对重要性是不同的。评价指标之间的这种相对重要性的大小，可用权重系数来表示。若wj是评价指标xj的权重系数，一般应该有
其中
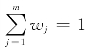
很显然，当被评价对象及评价指标（值）都给定时，综合评价（或对各被评价对象进行排序）的结果就依赖于权重系数了。即权重系数确定的合理与否，关系到综合评价结果的可信程度，因此，对权重系数的确定应特别谨慎。权重系数确定可以有直接方法和间接方法两种。
（一）直接方法
1．直接评分法
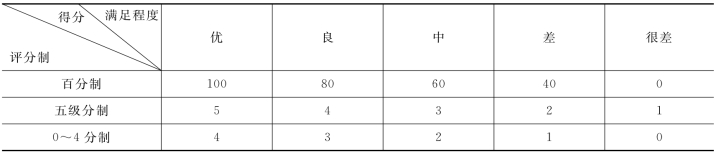
这种方法是由专家对各评价指标的重要程度分别打分，每一评价指标的得分与该指标得分之和对比，即为该评价指标的权重，见表10-1。
表10-1 工程综合评价评分等级和标准
【例10-1】评价某工程的经济效益，包括3个评价指标：工程造价（甲）、运输费用（乙）、工期（丙），表10-2便是7个专家对这3个评价指标不同的评分，采用百分制，试计算各个评价指标的权重。
表10-2 专家评分结果
解：此题直接评分，计算各个评价的权重，计算表格见表10-3。
表10-3 专家评分结果
总得分=619+608+624=1851。
检验权重=0．3344+0．3285+0．3371=1，符合条件。
工程造价指标权重为0．3344，运输费用指标权重为0．3285，工期指标权重为0．3371。
2．数值对比法
数值对比法是将各评价因素的重要性作两两比较后，按重要程度的差别打分，而后对各评价指标计算得分，将每一评价指标的得分与该因素得分之和对比，即为该评价指标的权重。这里我们介绍04评分法：将所有指标一对一地进行比较，非常重要的一方给4分，另一方给0分；比较重要的一方给3分，另一方给1分；双方同样重要，各给2分。以上每种情况里双方都共得4分，然后按每一指标的评分值占所有指标评分值总和的百分比确定其权重。在下边的例题中，可以通过比较1、2、3、4、5、6各个指标之间的关系，确定它们之间的分值。
【例10-2】评价某工程的经济效益，包括6个评价指标：工程造价（1）、运输费用（2）、安全费用（3）、工期（4）、施工设备（5）、施工环境（6），采用0～4分制，试用04评分法进行计算。
解：总得分=9+15+15+9+9+3=60。
权重=0．15+0．25+0．25+0．15+0．15+0．05=1，符合条件（见表10-4）。
表10-4 04评分法计算表
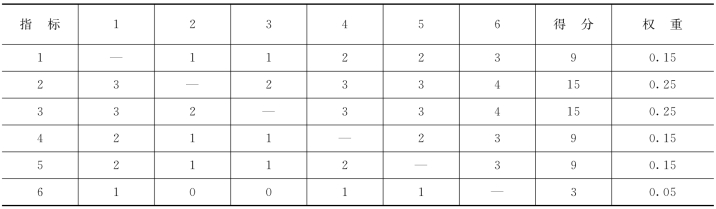
注意：在表中，如果指标1同指标3比为1∶3，则第一排第三列为1分，第三排第一列为3分。
3．比值评分法
数值对比法需要作的两两比较的次数较多，n个因素需作n（n-1）/2次，而应用比值评分法可以减少比较次数。比值评分法是将各评价因素自上而下排列，作出各评价因素对下一评价因素的重要度比值（重要度倍数），称为暂定重要性系数。设最后一个评价因素的得分为1，按上述关系逐项自下而上计算得分，并在此基础上对暂定重要性系数进行修正，将每一项评价因素的修正重要性系数与所有因素得分之和进行比较，即为各评价因素的重要性系数，即权重。
（二）间接方法
间接方法包括统计资料确定法、经验确定法等。其中，经验确定法是根据专家们的经验、智慧来判断确定，采用集思广益的方法确定重要性系数。经验确定法中包括两种依靠集体评分方法：专家会议法和德尔菲法。专家会议法是召集有关的专家开会，面对面地讨论、研究，来共同确定权重。德尔菲法是将所要预见或评价的问题及必要的背景材料，以函询方式请有关专家对提出的问题进行独立推测和判断。这些专家之间互相不能直接交换意见。得到的意见经综合归纳，匿名反馈给专家，进一步征询意见。如此反复多次，最后得出预测或评价结论。
五、综合评分法
（一）基本思路
综合评分法是目前采用较多的一种方法，也是较简单的一种方法。它是对各目标给出一个分值，计算各个方案的最后得分，根据得分的高低评价方案，得分越高，方案越优。综合评分值的计算，只是为了达到综合评价的目的，数值本身并无实际意义。
（二）综合评分法的一般步骤
（1）根据方案的评价目标，分解为若干个评价目标及若干层次的评价目标，大目标下还可分解子目标。
（2）对每一因素的达到程度定出若干等级，对每一等级制定一个评分标准。各等级的评分，可以等差，也可以不等差，根据需要而定。等级及其标准的确定有多种方法，常见的有百分制、五级分制、0～1分制以及0～4分制等，见表10-1。
（3）按照评分标准对各因素分别进行打分评价。
（4）经过计算、汇总，对方案加以比较选优。
综合评分法适用于目标关系简单的方案评价，方案与目标直接相关可直接得到方案对各目标的分值。而且一般来说，目标是并列的，其权重之和为1。
（三）综合评分法计算
如前所述，多指标综合评价，就是指通过一定的数学模型将多个评价指标值合成为一个整体性的综合评价值。可用于合成的数学方法较多。问题在于我们如何根据评价准则及被评价系统的特点来选择较为合适的合成方法。下面就几种常用的合成方法的数学模型、应用场合、特点等作一简要概述。即采用综合评分法进行计算。
1．综合评分法
（1）重要程度相同的加法评分法。综合评分法也可称为线性加权综合法（或加法合成法），它是根据评分标准对各因素评分，将得分相加求其总和或总平均值，以总和或总平均值最高者为最优方案。计算公式为
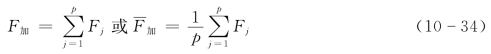
式中 F加——各项评价标准的得分总和；
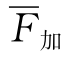——各项评价标准得分的总和平均值；
Fj——第j项评价标准得分值；
p——评价标准的数目。
【例10-3】计划修建黄河三号桥来改善两岸的交通，该工程有5个方案进行选择，经过一系列的实验与计算，得出这5种方案各项评价标准的评分值，见表10-5，运用加法评分法进行综合评价，选出最优方案。
表10-5 黄河三号桥各项评价标准评分值
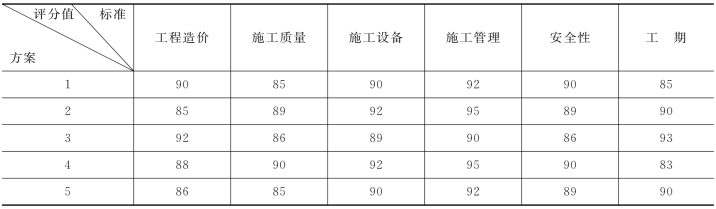
解：根据题意，进行计算。
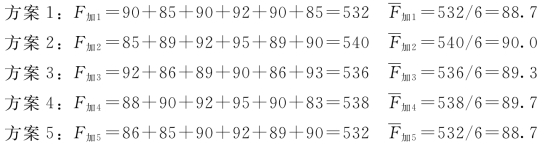
如上计算可得评价值以方案2的最高，因此方案2为最优方案。
（2）加权加法评分法。式（10-34）假设每项评价标准的重要程度相同，但在实际工作中，标准的重要性程度往往是有差别的，有些标准很重要，有些标准不太重要，甚至可以不予考虑。这时就不能直接应用式（10-34），而应视其重要性的不同而给以不同的重要性系数，这就是权重。若重要程度大，则权重就大；若重要程度小，则权重就小。
用w表示权重，则考虑了重要程度的加法评分法的计算公式为
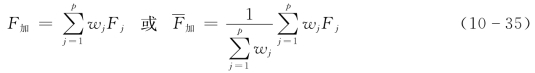
加权加法评分法能更符合实际，但权重wj的确定却是一个问题。
2．非线性加权综合法
所谓非线性加权综合法（或乘法评分法）是指应用非线性模型。所谓乘法评分法，就是根据评分标准对各因素评分，将得分连乘求积或几何平均值，以连乘积或几何平均值最大值为最优方案。其计算公式为
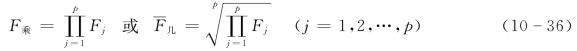
式中 F乘——各项评价标准得分的连乘积；
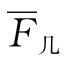——各项评价标准得分的几何平均值。
式（10-36）适用于评价标准重要性程度相同时的情况。若评价标准的重要性不一样，则需要考虑去权重，计算公式为
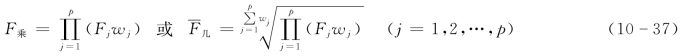
式（10-36）称为简单乘法评分法计算公式，式（10-37）称为加权乘法评分法计算公式。
【例10-4】题目同[例10-3]，运用加法评分法进行综合评价，选出最优方案。
解：根据题意，进行计算。
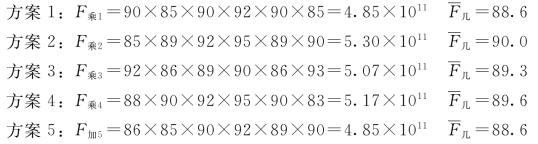
如上计算可得评价值以方案2的最高，因此方案2为最优方案。
3．加乘混合评分法
加法评分法和乘法评分法都是比较简单的方法，都有不同的局限性，于是可以将加法评分法和乘法评分法相结合，不仅避免了两者的缺点，而且同时具备了二者的优点，这样的方法称为加乘混合评分法。该方法将各方案的算术平均值与几何平均值之和作为该方案的总分，计算公式为
式中 F混——混合评分的分值；
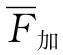——各项评价标准得分的总和平均值；
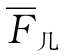——各项评价标准得分的几何平均值。
【例10-5】题目同[例10-3]，运用加乘混合评分法进行综合评价，选出最优方案。
解：根据题意，进行计算。
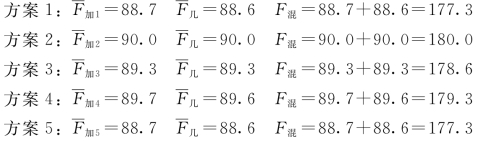
如上计算可得评价值以方案2的最高，因此方案2为最优方案。
【例10-6】计划修建黄河三号桥来改善两岸的交通，该工程有5个方案进行选择，经过一系列的实验与计算，得出这5种方案各项评价标准的评分值，见表10-6，运用加法评分法进行综合评价，选出最优方案。
表10-6 黄河三号桥各项评价标准评分值
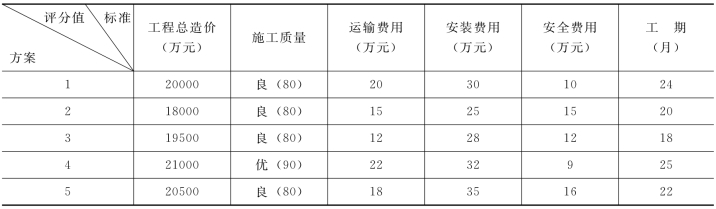
解：由实际情况可知，工程造价越高，施工质量越低，运输费用越高，安装费用越高，安全费用越高，工期越长，则效果值越低。
另外这里对定性指标进行量化效果值换算：“优”代表90，“良”代表80。对于其他的标准进行评分，例如工程总造价：最高的是20000元，对应的是100分；最低的是18000元，对应的是0分，中间的评分进行线性计算，见表10-7。
表10-7 工程综合评价计算
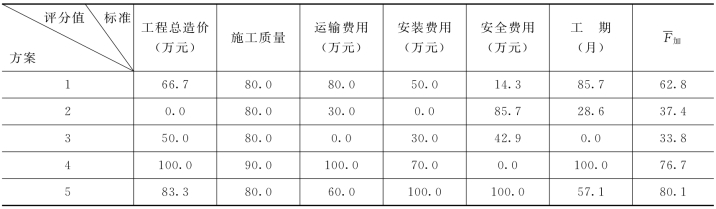
最后进行比较选优，可见方案5分值最高，为80．1，故选择方案5。
综上所述，综合评分法计算简单，应用比较普遍。
4．除法评分法
在前边所说的指标中，常常有一些指标要求越大越好，但是同时也存在另一些指标要求越小越好，如反映劳动消耗和劳动占用的指标。于是可以采用除法计算综合单指标评分值，能更加直观地反映评分值的大小。除法计算公式为
式中 F除——除法综合评分法；
fi、wi——要求越大越好的指标的得分和权重值；
fj、wj——要求越小越好的指标的得分和权重值；
m、n——要求越大越好和要求越小越好的指标的数目。
采用除法计算综合单指标评分值，评价方案的指标应能区分出越大越好和越小越好两类。
5．最小二乘评分法
这种方法是先对每个指标设定一个理想值，然后按式（10-40）计算综合指标评分值。计算结果数值越小，说明方案越好。
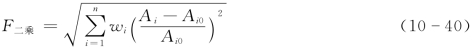
式中 F二乘——最小二乘法综合评分值；
Ai0——第i项指标的理想值；
Ai——第i项指标的实际值。
六、标准分法
不同的综合评价方法，有其自己的优缺点，即使是主成分分析法也有其难以克服的缺点。首先是综合后指标的经济意义不容易解释，尤其是当成分的因子负荷符号有正有负时，更难以解释；其次是这种方法太复杂，在实际工作中没有得到真正的采用。这里介绍标准分法，它的思想来源于计算高考学生总成绩的方法。高考中数门课程，简单代数和不能准确反映考生的实际水平（每门课程的重要程度及复杂程度不同）。对于考试成绩，以标准差的倒数（1/s）作为权数来计算考生的标准分。公式为
式中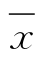
——平均成绩；
a、b——分项系数，根据实际情况，取值不一样。
将标准分评价运用到多指标综合分析问题中，即将每一个指标相对于一门课程，根据具体问题和相应指标的多少、大小，可适当调整基数a、b。同时将标准法运用到工程中可以进行计算。例如对10个建筑各自的工程造价、运输费用、工期、安全费用、施工条件5项指标
