3.8.3 城市水务系统层次性模糊评价法
3.8.3.1 层次性评价指标模糊优选系统构成
设有n1，n2，…，nk 个城市，现对这k 个城市水资源开发利用系统F1，F2，…，Fk 进行模糊优选，分层次水资源开发、利用和保护的程度进行评价，其中模糊优选过程中共涉及城市水务运行效率及效益的33类目标，系统层次划分及相应目标特征值如图3.11所示。
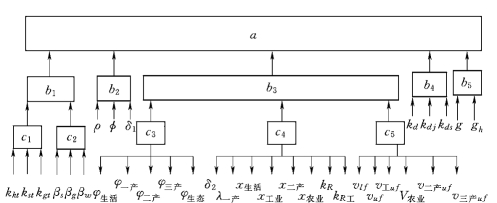
图3.11 城市水务系统水循环层次性评价指标结构图
a—城市水务系统；b1—水源子系统；b2—供水子系统；b3—用水子系统；b4— 排水子系统；b5—水处理与回用子系统；c1—水资源开发利用程度子系统；c2—水源构成子系统；c3—用水构成子系统；c4—用水效率子系统；c5—用水效益子系统
3.8.3.2 计算子系统中分系统对F1，F2， …，Fk 的相对优属度
现以c1 为例，对分系统c1 关于F1，F2，…，Fk 相对优属度优选过程进行论述。
3.8.3.3 确定目标kk，t、ks，t、kg，t对分系统c1 的重要性排序
对水源子系统b1 中开发程度c1 分系统中的三个目标kk，t、ks，t、kg，t，根据语气算子与模糊标度对应关系，设各目标之间二元比较的标度矩阵[35]为
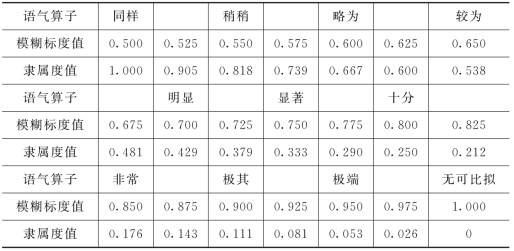
显然，所给的矩阵Ec1通过一致性检验。根据矩阵各行元素值之和，得到开发程度分系统中3个目标关于重要性的排序为：kk，t、ks，t、kg，t。其排序用语气算子与隶属度对应关系表示，见表3.2 （陈守煜，1994）。
表3.2 语气算子与模糊标度、隶属度对应关系表
3.8.3.4 确定kk，t、ks，t、kg，t对c1 重要性的相对隶属度即权重
以目标kk，t为标准，与目标ks，t、kg，t就分系统c1 进行重要性对比。经对比认为：kk，t比ks，t介于稍稍重要和略为重要之间；kk，t比kg，t介于较为重要和明显重要之间。根据语气算子与隶属度对应关系表3.2，得到kk，t、ks，t、kg，t对于分系统c1 的非归一化权生向量为
则可得到归一化权向量为
3.8.3.5 计算c1 关于F1， F2， …， Fk 的特征值矩阵Xc1的相对优属度
设c1 关于F1，F2，…，Fk 的特征值矩阵为
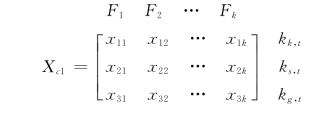
对越大越优目标采用公式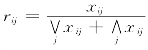
计算目标i相对优属度；对越小越优目标采用公式
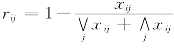计算其相对优属度。
其中，i=1，2，3，j=1，2，…，k，∨j xij、∧j xij分别表示就决策集j 对目标i的特征值取大或取小。
则Xc1变换为目标相对优属度矩阵：
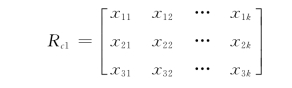
再根据优属度计算公式，决策j的相对优属度为
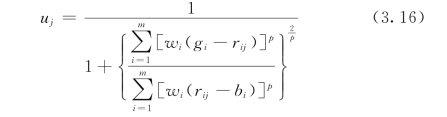
其中，根据参考系统中介过渡的两极具有最大相对优属度（优等决策的相对优属度）：
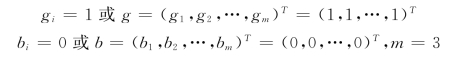
取p=2，即采用欧氏距离计算出c1 关于F1，F2，…，Fk相对优属度向量为
同理可计算c2 关于F1，F2，…，Fk 相对优属度向量为
c3 关于F1，F2，…，Fk 相对优属度向量为
c4 关于F1，F2，…，Fk 相对优属度向量为
c5 关于F1，F2，…，Fk 相对优属度向量为
3.8.3.6 计算子系统对F1， F2， …， Fk 的相对优属度
现以b3 为例，对子系统b3 关于F1，F2，…，Fk 相对优属度优选过程进行表述。
根据3.8.3.3同理可确定c3、c4、c5 对子系统b3 的归一化权向量为
由3.8.3.3中c3、c4、c5 关于F1，F2，…，Fk 相对优属度向量计算结果，可得到b3 关于F1，F2，…，Fk 相对优属度矩阵：
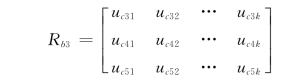
再由公式（3.16）计算可得b3 关于F1，F2，…，Fk 相对优属度向量为
同理可确定b1 关于F1，F2，…，Fk 相对优属度向量为ub1= （ub11，ub11，…，ub1k）。
根据3.8.3.3同理可计算b2 关于F1，F2，…，Fk 相对优属度向量为
b4 关于F1，F2，…，Fk 相对优属度向量为ub4 = （ub41，ub41，…，ub4k）；
b5 关于F1，F2，…，Fk 相对优属度向量为ub5 = （ub51，ub51，…，ub5k）。
3.8.3.7 计算总系统a关于F1， F2， …， Fk 的相对优属度
由公式（3.16）可知a 关于F1，F2，…，Fk 的相对优属度矩阵为
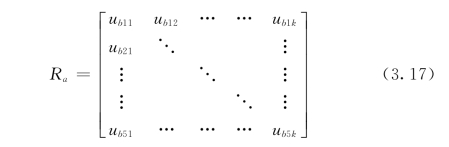
设b1、b2、b3、b4、b5 对a的归一化权向量wa = （wa1，wa2，wa3，wa4，wa5），根据公式（3.16）可确定总系统a关于F1，F2，…，Fk 的相对优属度为（ua）=（ua1，ua2，…，uak）。
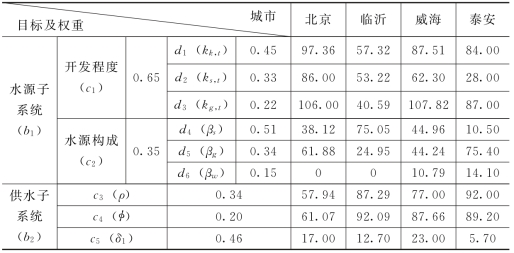
【案例3.2】 现以北京 （F1）、威海 （F2）、临沂 （F3）、泰安（F4）四个城市为例，分层次对四个城市水资源开发、利用和保护的程度进行评价，其目标特征值见表3.3。
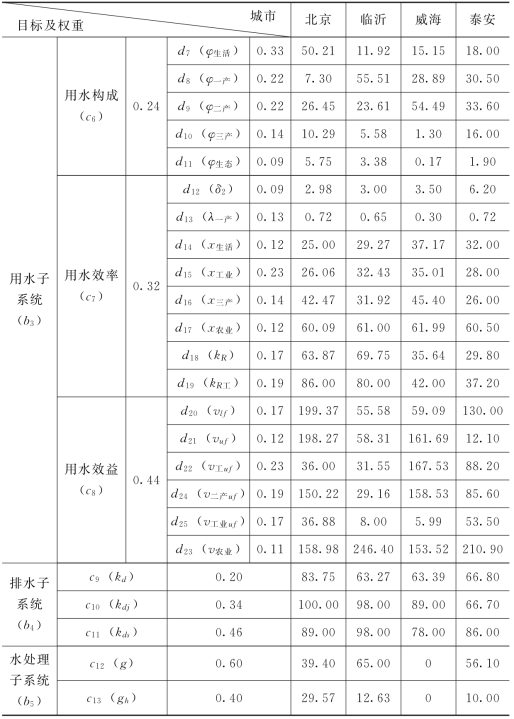
表3.3 北京、威海、临沂、泰安四城市水务系统目标特征值及权重计算表
续表
将四个城市水资源开发利用指标进行以上计算，可得总系统a关于F1、F2、F3、F4 的相对优属度矩阵为
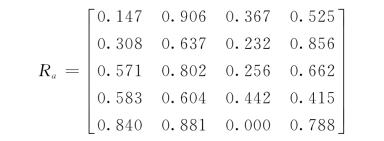
可设b1、b2、b3、b4、b5 对a的归一化权向量wa=（0.242，0.198，0.296，0.178，0.086），根据公式 （3.16），其中i=1，2，…5；j=1，2…，4；p=2，可确定总系统a 关于F1、F2、F3、F4 的相对优属度为
3.8.3.8 方案比较
为保证计算结果的精确性，对b1、b2、b3、b4、b5，5 个子系统取不同的权重，分别计算出a关于F1、F2、F3、F4 的相对优属度，计算过程中取用的权重及计算结果见表3.4。
表3.4 不同权重决策方案比较表
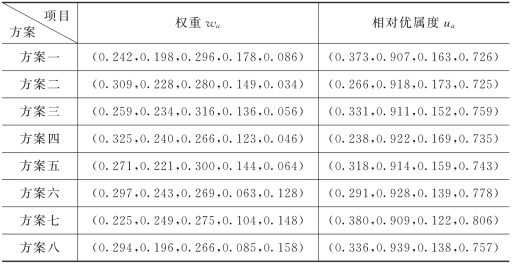
由矩阵Ra 及方案比较表可知，当对水源、用水、排水、水处理与回用子系统单独分析时，其结果显示均为威海市相对优属度最高，即威海的水源、用水、排水、水处理与回用四个子系统的运行效率及效益在四个城市中为比较好；单独分析供水子系统时，泰安市相对优属度最高，即泰安的供水子系统运行效率相对较高；综合分析整个水务系统时，采用8个不同的权重方案，其结论相同，均显示威海市相对优属度最高，即威海市水务系统运行效率及效益最高。从以上分析，可反映出所建模型的合理性，可作为城市水务系统进行效率及效益的评价依据。
运用系统模糊决策理论，建立城市水务系统运行及经济评价指标模型，在各决策目标特征值相差较大的情况下，能以各评价指标及各层次为出发点，分别从纵向及横向综合考虑各因素对城市水务系统运行的影响，确定城市水务系统及其子系统运行效率的高低，找出其中运行效率较低的环节，为城市水务系统改革提供决策性和可操作性依据。