5.4.4　水权初始配置的相关机会多目标规划模型

5.4.4　水权初始配置的相关机会多目标规划模型

5.4.4.1 问题的提出

城市水务管理的重要工作之一就是如何协调统一开发利用各类水源，公平合理地分配水资源使用权，解决水权分配中出现的不确定性问题。并应考虑到水资源量、用水量和用水要求等要素均具有随机性变化的特性、特征，而传统的优化计算方法是采用线性或非线性规划法；对于一些简单的机会约束模型，也是根据已知的置信水平，把机会约束转化为等价的确定性约束（方红远等，2002），对涉及多个概率分布随机变量的组合，要求出这些复杂组合的概率特定值就比较困难了，因此，构建可以处理约束条件中含有随机变量的相关机会目标规划模型，是解决上述问题的有力途径之一。

5.4.4.2 模型结构

城市水源可概化为当地地表水、地下水和外调水3种水源，用水户可概化为生活用水、第一、第二、第三产业4 大类用水户，并可以进一步细分为各类用水，初始水权配置分级分类图见图5.1。本科题研究仅就上述3种水源、4大类用水户构建城市水权初始配置的相关机会多目标规划模型。

设水权初始配置量：X= {xi，j，i=1，2，3，4；j=1，2，3}

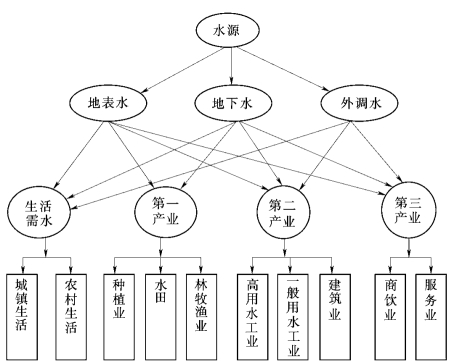
图5.1　初始水权配置分级分类图

3种水源能够提供的最大取水量为：Ws、Wg、Ww，并是随机变量，由式（4.1）知：

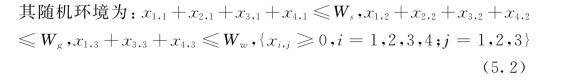
式中 xi，j——第i 类用水户分配到的第j 种水源水权量，m3；

Ws、Wg、Ww——地表水资源、地下水资源、外调水资源可供水量，m3；

Wsk、Wgk、Wwk——地表水资源、地下水资源、外调水资源可开发利用量，m3。

4大类用水户希望获得的水权数为：q生活、q一产、q二产、q三产，则有：

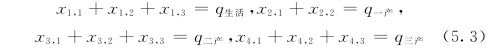
在式（5.4）中考虑到第一产业用水的效益较低，经济承受能力较弱，外调水不向其提供水源。上述等式说明水权分配决策应该满足四大类需水要求，由于水权分配系统的不确定性，在水权分配实现以前，并不能确定其决策是否真的能够实现，所以必须使用机会函数（5.4）去评价4大类用水户的需水权量。

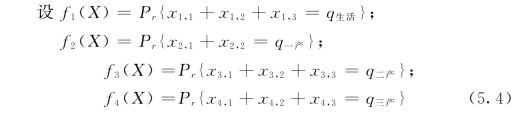
式中 Pr 表示在{·}中的事件成立的概率。

通常希望极大化4大类用水户需水权量的机会函数，以尽可能地提高用水户实现愿望的概率，所以，有城市初始水权配置相关机会多目标规划模型：

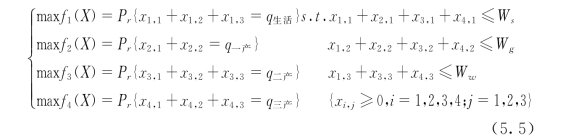
于是随机可行集S 的概率函数定义为：

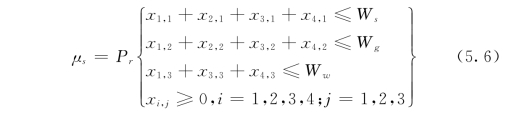
因{x1，1，x2，1，x3，1，x4，1}、{x1，2，x2，2，x3，2，x4，2}、{x1，3，x3，3，x4，3}3组水源水权决策变量是相互独立的，每一组中某用水户可能获的某种水源水权量（元素）是随机相关的，并且有相同的实现机会。同时有：

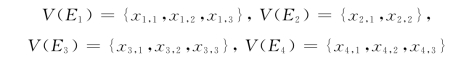
式中 V（Ei）表示满足i个事件 （用水户从各水源分配水权量）所必须的分量构成的集合，i=1，2，3，4。

定义E=E1∩E2∩E3∩E4，显然有V（E）= {xi，j，i=1，2，3，4；j=1，2，3}，由随机关系得到：

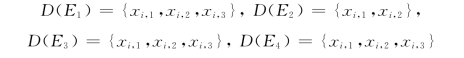
式中 D（Ei）——与V（Ei）中至少一个元素随机相关的分量构成的集合。

各类用水产需水权向量事件E1、E3、E4 的诱导约束为

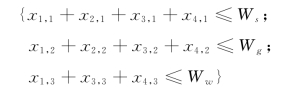
事件E2 的诱导约束为：

所以，对X∈E1∩E2∩E3∩E4，有：

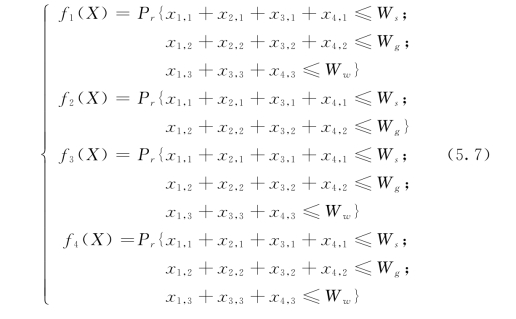
考虑城市水权初始配置的优先结构和目标值。

优先级1：满足进一步改善生活质量需水权数 （满足居民生活基本、生态环境需水应从一般经济性用水水权配置中相对分离，优先保障，以利水权市场化运作）的机会尽可能地达到P1，即：

Pr{x1，1+x1，2+x1，3=q生活}+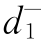 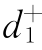－ =P1，其中 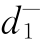将被极小化；

优先级2：满足第一产业需水权数的机会尽可能地达到P2，即：

Pr{x2，1+x2，2 =q一产}+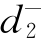 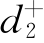－ =P2，其中 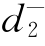将被极小化；

优先级3：满足第二、三产业需水权数的机会尽可能地达到P3、P4，即：

Pr{x3，1+x3，2+x3，3=q二产}+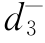 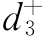－ =P3，其中 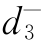将被极小化；

Pr{x4，1+x4，2+x4，3=q三产}+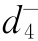 + 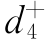=P4，其中 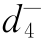将被极小化；

优先级4：尽可能少地从外地购买水权，即：

x1，3+x3，3+x4，3+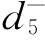 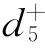－ =0，其中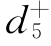 将被极小化。

因此，上述问题的相关机会目标规划模型为

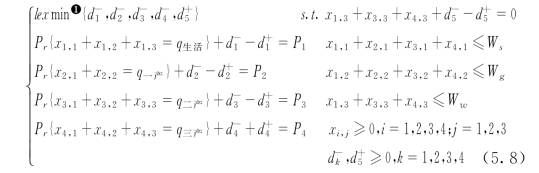
① lex min表示按词典序极小化目标向量。

5.4.4.3 模型求解

（1）拟定水资源总权量和用户需水权量。由确定城市的水资源可开发利用量（如多年平均量、某规划期平均量等）确定Ws、Wg、Ww；并拟定各类用户的需水权量期望值q生活、q一产、q二产、q三产。

（2）设置水资源量的随机分布函数和率定分布参数。按照水资源变化规律设置Ws、Wg、Ww 符合的概率函数 （如我国水资源变量一般符合皮尔逊Ⅲ型分布），并根据历年资料率定其分布参数。

（3）初步确定满足各类用水户需水要求的机会。组织专家、政府官员、用水户代表采取 “专家打分法 （Delphi法）”，确定P1、P2、P3、P4 值。

（4）基于随机模拟的遗传算法。一种基于随机模拟的遗传算法为求解相关机会目标规划模型提供了有效的手段[32]，即在上述（1）、（2）、（3）内容拟定后，根据对式 （5.7）的随机模拟，运用遗传算法就可给出城市水权初始配置的最优解，满足各类用户需水权量要求的机会 （概率）。其步骤如下：①选定种群规模pop_size、交叉概率Pc、变异概率PM 以及基于序的评价函数参数a=0.05，进化过程中每次随机模拟执行3000 次循环；②初始产生pop_size个染色体；③交叉和变异操作，并使用随机模拟技术来检验其后代的可行性；④使用随机模拟技术计算各染色体的目标值；⑤根据目标值，使用基于序的评价函数计算每个染色体的适应度；⑥旋转赌轮，选择染色体，获得新的种群；⑦重复步骤③到⑥，直到完成给定的循环次数；⑧选择最好的染色体作为最优解。如在计算中出现某种需水的满足机会或实际保证率不合适，某种需水的破坏深度太大时，应重新组织有关专家、政府官员、用水户代表参加的专家打分法 （Delphi法）”，确定保证率P1、P2、P3、P4 值；或者调整用水户的需水权量，并进行上述模拟计算，求得满意解。以此作为水权分配依据，为水权管理奠定基础。

案例 某市市区总面积为67km2，总人口63.8万人，其中建成区面积41.0km2，城区人口41.1万人，近郊区人口22.7万人。根据该市水资源开发利用规划知：地表水Ws=1095万m3，CV=0.75、CS=2CV；地下水Wg=5293万m3、CV=0.42、CS=2CV；外调水 （该市从城区外水库调水）WW =1825 万m3、CV=0.56、CS=2CV；年需水量q生活=1040万m3、q一产=1140万m3、q二产=4728万m3、q三产=1305万m3。采取 “专家打分法（Delphi法）”拟定保证率P1=0.95、P2=0.50、P3=0.95、P4=0.85值。

基于随机模拟遗传算法得出的该市水权分配最优解为x1，1=96万m3，x1，2=698万m3，x1，3=246万m3，x2，1=757万m3，x2，2=383 万m3，x3，1=133 万m3，x3，2=3219 万m3，x3，3=1376万m3，x4，1=109 万m3，x4，2=993 万m3，x4，3=203 万m3；其中满足生活、第一产业、第二产业、第三产业需水权要求的机会或实际保证率分别为97%、48%、96%、86%，基本达到了比较合理地配置水资源的目的。

在实际工作中，可以上述初始水权分配数为依据，按照各年来水量的丰枯情况，按比例分配实际水权量的多少，所以，应将上述水权分配最优解理解为水权分配指标，并作为水权管理的定量依据。