5.2 探索性因子分析
在5.1节中,相关分析结果显示,测试成绩在或高或低的程度上两两相关。鉴于这些测试对应的是阅读能力或与阅读能力相关的语言因素,所以为了能够清楚地反映这些测试及其所代表的构念之间关系的亲疏远近,一目了然地展现其间的内在结构,以便考察阅读能力的潜在结构,笔者接下来进行探索性因子分析(EFA)。
EFA是一种降维处理技术,它从数据出发,首先计算原始变量的相关矩阵或协方差矩阵(covariance matrix),然后利用原始变量的线性组合形成几个综合指标(即共同因子),从而把原始变量之间错综复杂的关系加以简化,以揭示数据的基本结构和本质特征。
因子分析有EFA和验证性因子分析(confirmatory factor analysis,CFA)之分。结构方程模型中的测量模型,其实质就是CFA。随着SEM技术及其分析软件的成熟完善和普及推广,许多研究开始采用CFA进行阅读成分分析(例如:Shiotsu,2010;Van Gelderen et al.,2007)。笔者之所以在这里不用CFA,是因为与以数据为驱动的EFA不同,CFA的模型设定以较为严谨的理论或较为充分的实证研究为基础,在阅读能力尤其是阅读流利性这个研究尚不充分的领域中,如果使用CFA,初始模型会由于理论或实证基础不够坚实而不得不过度修正。事实上,有些定量研究的专家已经指出,这样探索性地使用CFA与CFA的使用条件相悖,应该换用EFA(例如:Asparouhov & Muthen,2009)。
因为表5-2已经呈现原始变量的相关矩阵,所以接下来笔者首先计算KMO测度(Kaiser-Meyer-Olkin Measure of Sampling Adequacy)值和进行Bartlett球体检验(Bartlett's Test of Sphericity),以判断数据是否适用于因子分析。KMO测度值越高,越接近1,表示原始变量间的相关性越强,共同因子对原始变量的解释力越大。通常,因子分析要求KMO测度值不小于0.7(张文彤,2004)。Barlett球体检验以原始变量相互独立为假设,如果检验结果的显著水平小于0.05则可以拒绝该假设,即原始变量之间显著相关,能够提取共同因子。在本研究中,KMO测度值是0.914,Bartlett球体检验的显著水平小于0.001(近似卡方=1 580.416,自由度=78),说明非常适合进行因子分析。
表5-2 测试成绩的相关分析
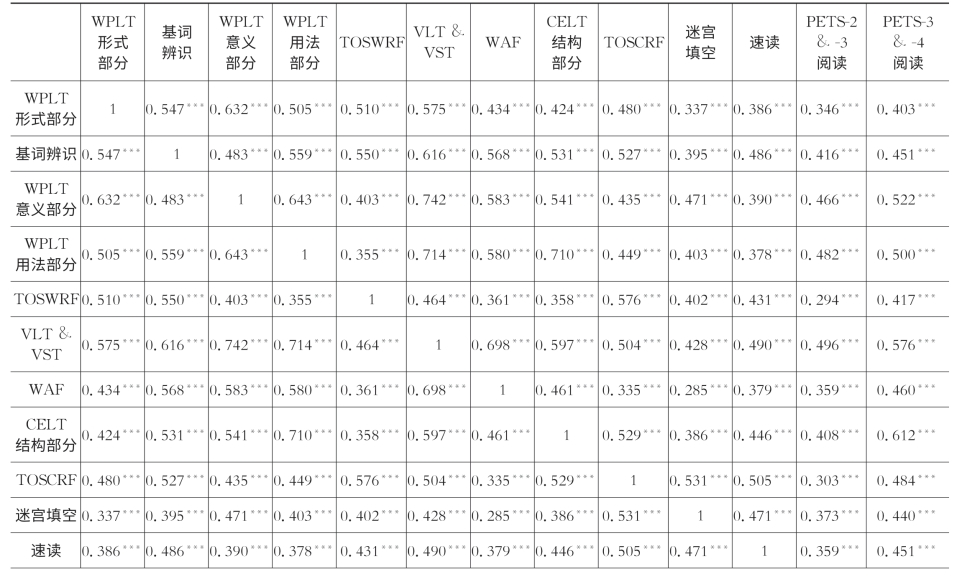
(续表)
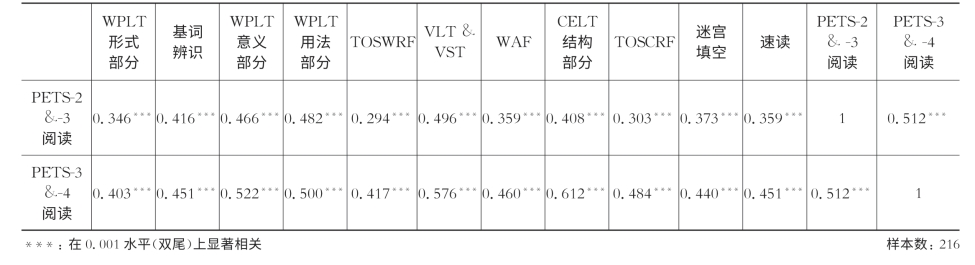
然后用以主成分分析(principal component analysis)为因子的提取方法、以方差最大正交旋转(varimax)为因子的旋转方法进行探索性分析,结果显示有两个因子的特征值(eigenvalue)大于1的标准(旋转前是6.767和1.102,旋转后是4.548和3.321),它们的累计方差贡献率是60.531%(旋转前两个因子所解释的方差分别占总方差的52.050%和8.481%,旋转后是34.983%和25.548%),也就是说笔者成功地提取了两个因子。各项测试成绩的因子负荷(factor loading)如表5-3所示:
表5-3 测试成绩的因子负荷
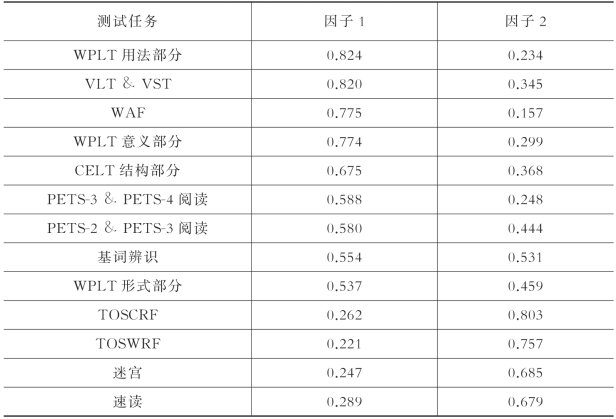
如表5-3所示,形态意识的四项测试、词汇广度测试、词汇深度测试、语法知识测试和理解准确性的两项测试与因子1的关系密切,其因子负荷介于0.537和0.824之间。在二语领域,词汇知识(包括词汇广度和词汇深度)和语法知识与阅读理解相关已经基本成为共识(Jeon & Yamashita,2014),关于形态意识与阅读理解关系的研究尽管数量相对较少,但是研究结果基本一致,即前者能够预测后者(Jeon,2011;Kieffer & Lesaux,2012b)。换而言之,这些构念的共同之处在于对文字所表达意义的理解。并且在已有的研究以及本研究中,阅读理解、词汇知识、语法知识和形态意识的测量以准确性为指标,没有考虑时间和速度的问题。根据以上分析,笔者把因子1命名为理解准确性。
在表5-3中,单词识别测试和阅读流利性的三项测试与因子2的关系密切,其因子负荷介于0.679和0.803之间。在本研究中,单词识别以效能(即单位时间内的准确性)而非单纯的准确性为测量指标,因此它在本质上是阅读单词的流利性。也就是说,因子2代表了阅读流利性。
