5.3.3 结构模型
根据模型中的变量对应一个还是多个观察指标,结构模型分为三种:完全潜在模型,即模型中的所有变量都有多个观察指标;部分潜在模型,即模型中既有多指标的变量也有单指标的变量;完全显性模型,即模型中的所有变量都只有一个观察指标。在结构方程模型中,测量模型的实质是因子分析,结构模型的实质是路径分析。传统的以回归为方法的路径分析基本上处理的都是完全显性模型处理的问题。
本研究的结构模型属于第二种,即部分潜在模型。模型中共有七个变量:形态意识、阅读流利性和理解准确性是多指标的潜在变量,单词识别、词汇广度、词汇深度和语法知识只有一个观察指标。对于结构模型中的单指标变量,AMOS的处理方法有两种:一种是直接以观察变量的形式呈现,另一种是以潜在变量的形式呈现,然后在测量模型中设置它的一个观察指标。因为两种方法的最终分析结果一样,而第二种方法在参数设置和图形呈现上都较为麻烦,所以本研究采用第一种方法,即在AMOS绘制的结构模型中既有椭圆形的潜在变量也有长方形的观察变量,吴明隆(2010)称其为混合变量的路径分析。
为回答4.1.2节中的问题,本研究共需构建四个模型:模型一对应第二个问题,模型二对应第三个问题,模型三对应第四和第五个问题,模型四对应第六个问题。在这些模型中,模型三是本研究的重点。
5.3.3.1 模型一
在表5-6中,形态意识、单词识别、词汇广度、词汇深度和语法知识都与阅读流利性显著相关。那么在控制单词识别、词汇广度、词汇深度和语法知识之后,形态意识是否仍然能够直接地、独立地影响阅读流利性呢?为了回答这个问题,我们构建了如图5-3所示的假设模型:
模型辨识的结果显示:有两条路径的回归系数不显著,分别是从词汇深度到阅读流利性(β=-0.118,p=0.216)和从形态意识到阅读流利性(β=0.24,p=0.14)。删除它们之后,虽然剩下的路径在统计上都具有显著意义,但是模型的各个整体适配度指标都通不过检验。因此,根据AMOS输出报表中的修正指数,把单词识别、词汇广度和语法知识三个自变量的测量误差设定为两两共变的关系,即依次在e9与e11之间、e8与e9之间以及e8与e11之间建立起相关。
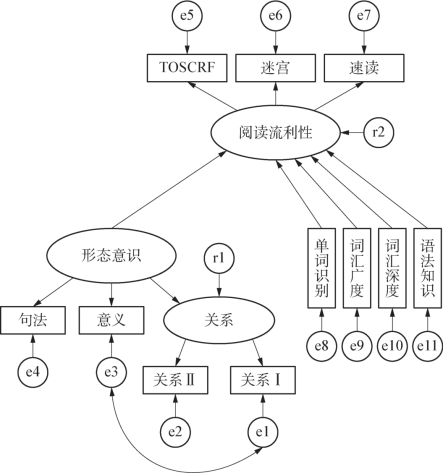
图5-3 假设的模型一
这三组变量的释放既有实证数据的支持又能够在理论上得到解释。在表5-6中,词汇广度与语法知识的相关系数是0.597,单词识别与词汇广度的是0.464,单词识别与语法知识的是0.358。词汇广度与语法知识相关,是因为语法知识涉及对短语、从句和句子这些较大语言单位的分析,而这些较大的语言单位是由单词按照一定的规则组合而成。词汇量越大,生词越少,越有助于学习者分析句子的结构,理解句子的意义。单词识别与词汇广度两个概念的核心都是单词,词汇量越大,学习者在单位时间内能够识别的单词越多,两者存在一定程度的相关。至于单词识别与语法知识,两者的相关程度较低,但是快速、准确的单词识别对语法知识的熟练掌握和运用仍然具有促进作用。
按照上述步骤对假设模型修正后,再次进行模型辨识,结果如图5-4所示:
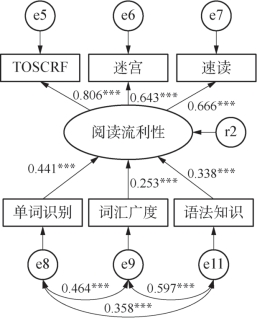
图5-4 修正后的模型一
***:p≤0.001
对修正后的模型进行评估,结果显示拟合度良好。为节约空间,在此只列出绝对和增值适配度指标的数值:x2/df=1.432(<2),GFI=0.987(>0.9),AGFI=0.953(>0.9),RMSEA=0.045(<0.08),CFI=0.994(>0.9),NNFI=0.986(>0.9)。
5.3.3.2 模型二
在表5-6中,形态意识、单词识别、词汇广度、词汇深度、语法知识和阅读流利性均与理解准确性显著相关。那么在控制单词识别、词汇广度、词汇深度、语法知识和阅读流利性之后,形态意识是否仍然能够直接地、独立地影响理解准确性呢?为了回答这个问题,笔者构建了如图5-5所示的假设模型:
模型辨识的结果显示:有三条路径的回归系数不显著,分别是从形态意识到理解准确性(β=0.094,p=0.619)、从词汇深度到理解准确性(β=0.094,p=0.391)和从单词识别到理解准确性(β=0.091,p=0.336)。虽然剩下的路径在统计上都具有显著意义,但是模型的各个整体适配度指标都通不过检验。因此,根据AMOS输出报表中的修正指数,依次释放了词汇广度和语法知识、词汇广度和阅读流利性、语法知识和阅读流利性三组变量。
这三组变量的共变关系既有实证数据的支持又能够在理论上得到解释。在5.3.3.1节中,对词汇广度与语法知识的相关进行了说明,在此不再赘述。至于另外两组变量,如表5-6所示,词汇广度和语法知识与阅读流利性均显著相关(p<0.001),相关系数分别是0.669和0.648。词汇量越大,语法知识掌握和运用得越好,由生词和复杂句子结构造成的“卡壳”现象越少,阅读越能够顺畅地进行。
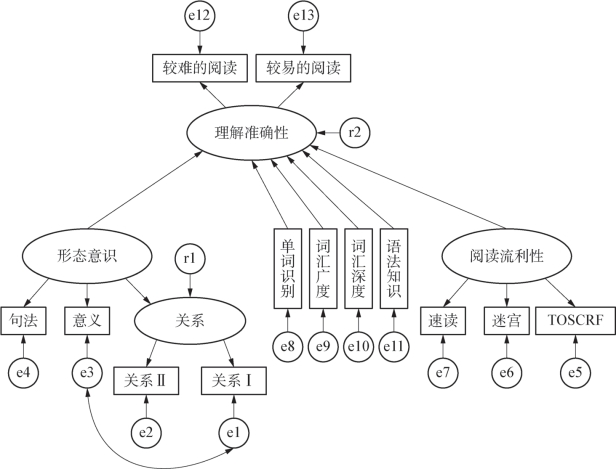
图5-5 假设的模型二
按照上述步骤对假设模型修正后,再次进行模型辨识,结果如图5-6所示:
对修正后的模型进行评估,结果显示拟合度良好。为节约空间,在此只列出绝对和增值适配度指标的数值:x2/df=1.469(<2),GFI=0.981(>0.9),AGFI=0.946(>0.9),RMSEA=0.047(<0.08),CFI=0.992(>0.9),NNFI=0.983(>0.9)。
5.3.3.3 模型三
模型三是本研究的重点。如表5-6所示,本研究的七个潜在变量两两相关,这说明形态意识能够以单词识别、词汇广度、词汇深度和语法知识中的任何一个为中介影响阅读流利性,也能够以这些变量以及阅读流利性中的任何一个为中介影响理解准确性。那么,在控制这些中介变量后,形态意识是否仍然直接地、独立地影响阅读流利性和理解准确性呢?为了回答这个问题,笔者以第三章中的概念框架为理论指导,以已经构建的测量模型(见图5-2)为基础,假设完整的结构方程模型如图5-7所示:
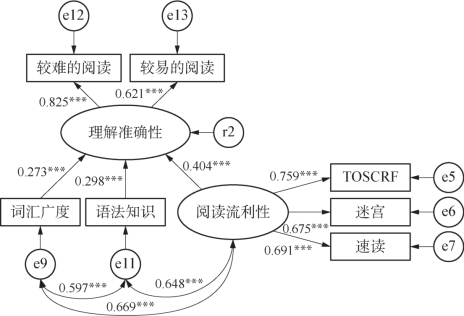
图5-6 修正后的模型二
***:p≤0.001
**:p≤0.01
如图5-7所示,形态意识影响阅读流利性的路径有四条,分别以单词识别、词汇广度、词汇深度和语法知识为中介;形态意识影响理解准确性的路径有八条,其中四条是在间接影响阅读流利性的基础上再以阅读流利性为中介,另外四条是以单词识别、词汇广度、词汇深度和语法知识为中介。
模型辨识和评估的结果显示,假设模型能够通过变量正态性、基本适配度和内在结构适配度的检验,但是在整体适配度的检验中,x2/df、AGFI和RMSEA三项指标达不到标准,具体数值分别是2.826、0.843和0.092,GFI和NNFI刚刚满足要求,分别是0.907和0.908。这说明图5-7的假设模型需要修正。
首先,对路径的回归系数是否具有显著意义进行查看,依次删除了从单词识别到理解准确性(β=-0.012,p=0.893)、从词汇深度到阅读流利性(β=-0.065,p=0.374)、从词汇深度到理解准确性(β=0.078,p=0.298)三条在统计上不具有显著意义的路径。
然后,根据AMOS输出报表中的修正指数,同时结合这些指数所建议的修正路径是否能够得到合理的解释,依次释放了两组变量:一组是形态意识的关系维度与单词识别,另一组是形态意识的句法维度与语法知识。换而言之,设定图5-7中“关系”的残差与“单词识别”的测量误差、“句法”的测量误差与“语法知识”的测量误差具有共变关系,即在r1与e10之间、e4与e13之间建立相关。在5.6.3节中,将对这两条相关路径的增设进行详细的解释。
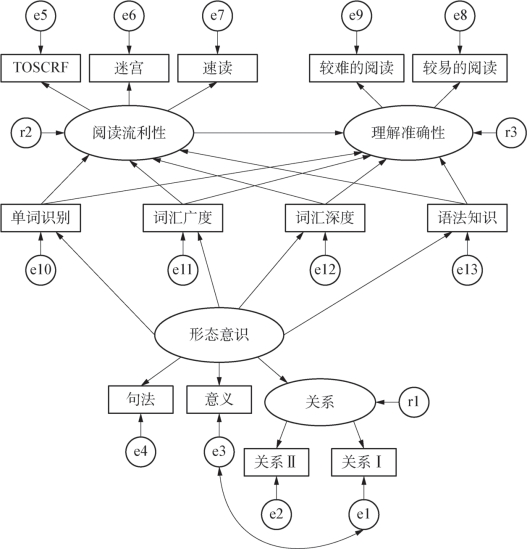
图5-7 假设的模型三
在删除了三条不具有显著意义的路径和增设了两条相关路径之后,再次进行模型辨识,结果如图5-8所示:
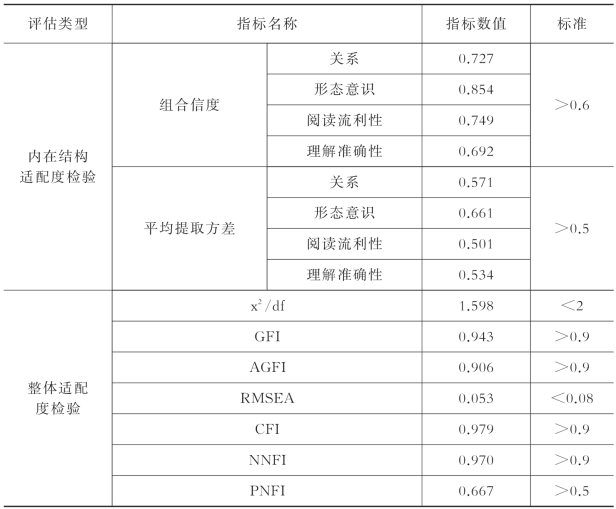
对修正后的结构方程模型进行评估,结果显示拟合度良好。表5-7列出了各项指标的具体数值:
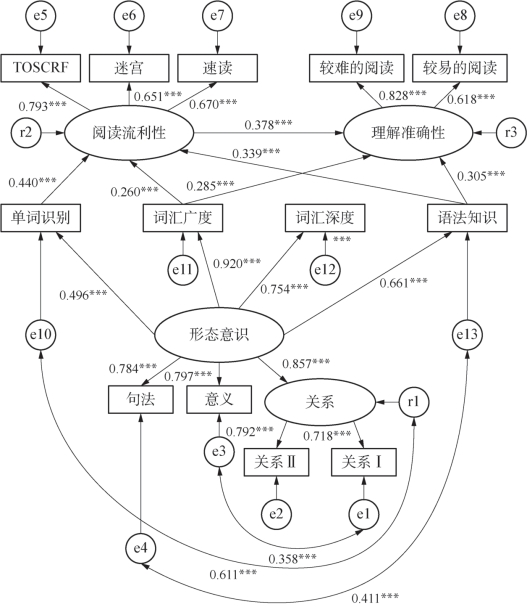
图5-8 修正后的模型三
***:p≤0.001
表5-7 修正后模型三的评估结果

(续表)
在最终确定是否接受如图5-8所示的模型之前,需要讨论几个相关的问题,以尽可能准确地描述形态意识与阅读能力之间的关系。
第一个问题是:除了以单词识别、词汇广度和语法知识为中介,形态意识能否直接地、独立地影响阅读流利性?为了回答这个问题,在图5-8中增加了一条从“形态意识”指向“阅读流利性”的单箭头路径。模型辨识的结果显示:新路径的出现导致词汇广度对阅读流利性的影响由显著(β=0.26,p<0.001)转为不显著(β=0.029,p=0.886);其他原有路径的系数和显著水平改变不大;新路径本身的回归系数在统计上不具有显著意义(β=0.294,p=0.224)。如果删除从词汇广度到阅读流利性这条路径,那么结果如图5-9所示,从形态意识到阅读流利性这条路径由不显著转为显著(β=0.327,p<0.001)。
对图5-9进行模型评估,然后比较它与图5-8的评估结果,笔者发现两个模型的适配度差别极小,可以忽略不计。也就是说,从统计上讲,两个模型都可以接受。但是因为两个模型的适配度差别不大,所以图5-9中形态意识对阅读流利性的直接影响实际上等价于图5-8中被删除的以词汇广度为中介的间接影响再加上被削弱的以语法知识和单词识别为中介的间接影响。因此,从理论上讲,图5-8更好地反映了形态意识影响阅读流利性的内部机制。综上所述,图5-8优于图5-9,说明在考虑了单词识别、词汇广度和语法知识的中介效应之后,形态意识对阅读流利性没有直接和独立的影响,同时也排除了形态意识直接影响阅读流利性后间接影响理解准确性(即形态意识→阅读流利性→理解准确性)的可能。
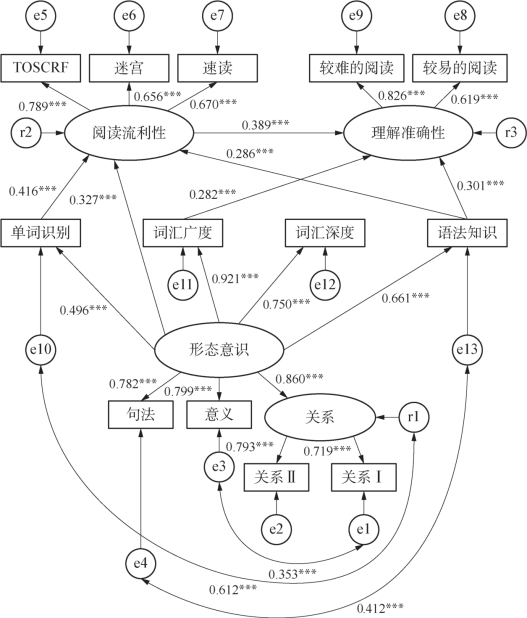
图5-9 模型三的检验模型1
***:p≤0.001
第二个需要回答的问题是:除了以图5-8中的路径方式间接地产生效应,形态意识是否能够直接地、独立地影响理解准确性?为此,在图5-8中增加了一条从“形态意识”指向“理解准确性”的单箭头路径。统计结果显示:新路径的加入使模型原有的其中三条路径发生了较大变化,即词汇广度对理解准确性的影响由显著(β=0.285,p<0.001)转为不显著(β=0.011,p=0.958)、语法知识对理解准确性的影响降低并且具有显著影响的概率减小(β=0.305,p<0.001变为β=0.256,p=0.004),阅读流利性对理解准确性的影响降低并且具有显著影响的概率减小(β=0.378,p<0.001变为β=0.344,p=0.002);同时,新路径本身的回归系数在统计上不具有显著意义(β=0.362,p=0.15)。如果删除从词汇广度到理解准确性这条路径,那么结果如图5-10所示:尽管从阅读流利性到理解准确性和从语法知识到理解准确性这两条路径或者没有变化或者变化极小,显著水平仍然都大于0.001(前者仍然是β=0.344,p=0.002,后者是β=0.255,p=0.003),但是从形态意识到理解准确性这条路径由不显著转为显著(β=0.374,p<0.001)。
对图5-10进行模型评估,然后比较它与图5-8的评估结果,笔者发现两个模型的适配度差别极小,可以忽略不计。也就是说,从统计上讲,两个模型都可以接受。但是因为两个模型的适配度差别不大,所以图5-10中形态意识对理解准确性的直接影响实际上等价于图5-8中被删除的以词汇广度为中介的间接影响再加上被削弱的以语法知识为中介的间接影响和先以单词识别、词汇广度和语法知识为中介再以阅读流利性为中介的间接影响。因此,从理论上讲,图5-8更好地反映了形态意识影响理解准确性的内部机制。综上所述,图5-8优于图5-10,说明在考虑了单词识别、词汇广度、语法知识和阅读流利性的中介效应之后,形态意识对理解准确性没有直接和独立的影响。
在构建图5-9和图5-10两个模型的过程中,笔者发现无论是增加从“形态意识”直接到“阅读流利性”还是直接到“理解准确性”的路径,图5-8中受影响最大的都是以“词汇广度”为中介的路径,由显著转为了不显著。究其原因主要是形态意识与词汇广度联系密切,从“形态意识”到“词汇广度”的路径系数高达0.92左右。
在与图5-9和图5-10比较之后,最终确定图5-8是最佳模型,对形态意识与阅读流利性和理解准确性关系的描述最准确。因此接下来对图5-8的AMOS计算结果进行报告和说明。
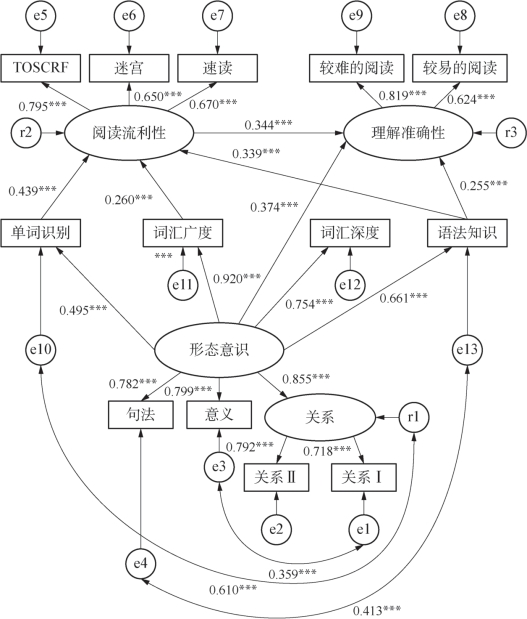
图5-10 模型三的检验模型2
***:p≤0.001
**:p≤0.01
图5-8是一个完整的结构方程模型,其中结构模型中的数值表示各条路径的标准化回归系数,也称β系数,即路径一端的外衍变量对另一端内衍变量的直接效应(direct effects)。例如,阅读流利性对理解准确性的直接效应是0.378;也就是说,在保持其他影响理解准确性的变量不变时,阅读流利性增加一个单位的标准差,理解准确性随之增加0.378个单位的标准差。至于间接效应(indirect effects),是外衍变量对中介变量的直接效应与中介变量对内衍变量的直接效应的乘积。
在图5-8中,形态意识不直接影响阅读流利性,而是以单词识别、词汇广度和语法知识为中介间接地产生影响,其间接效应分别是:
●形态意识→单词识别→阅读流利性:0.496×0.440=0.218;
●形态意识→词汇广度→阅读流利性:0.920×0.260=0.239;
●形态意识→语法知识→阅读流利性:0.661×0.339=0.224。
形态意识对阅读流利性的总效应(total effects)是以上间接效应之和[6]:
0.218+0.239+0.224=0.681
同样,形态意识不直接影响理解准确性,而是以词汇广度和语法知识为中介间接地产生影响,同时又在间接影响阅读流利性后再以阅读流利性为中介对理解准确性产生影响,其间接效应分别是:
●形态意识→词汇广度→理解准确性:0.920×0.285=0.262;
●形态意识→语法知识→理解准确性:0.661×0.305=0.202;
●形态意识→单词识别→阅读流利性→理解准确性:0.496×0.440×0.378=0.082;
●形态意识→词汇广度→阅读流利性→理解准确性:0.920×0.260×0.378=0.090;
●形态意识→语法知识→阅读流利性→理解准确性:0.661×0.339×0.378=0.085。
形态意识对理解准确性的总效应(total effects)是:
0.262+0.202+0.082+0.090+0.085=0.721[7]
根据AMOS输出结果中的多元相关系数平方(squared multiple correlation)报表,单词识别、词汇广度和语法知识可以联合解释阅读流利性68.5%的方差,词汇广度、语法知识和阅读流利性可以联合解释理解准确性71.6%的方差。这说明图5-8中的模型包含了影响阅读流利性和理解准确性的主要变量。
5.3.3.4 模型四
在以上三个模型中,阅读流利性和理解准确性是两个相对独立的变量,这是为了清楚地展现它们之间的关系以及它们分别与形态意识的关系。但事实上,阅读流利性和理解准确性是阅读能力的两个维度。在本节中,笔者将增设阅读能力作为阅读流利性和理解准确性的高阶构念,框架式地讨论形态意识对阅读能力而不是对其具体构成的影响。以这种方式构建出的模型可以与图5-8相互验证,同时也能够更加清晰地显示中介变量对阅读能力效应的大小。为此,把图5-7中的假设模型改为如图5-11所示的模型。需要说明的是,在图5-11以及随后的图5-12和图5-13中,阅读能力是一个二阶的(或者说高阶的)潜在变量,阅读流利性和理解准确性是它的一阶(或者说低阶的)潜在变量。换而言之,阅读流利性和理解准确性处在阅读能力的测量模型之中,阅读能力是结构模型中的唯一内衍变量。
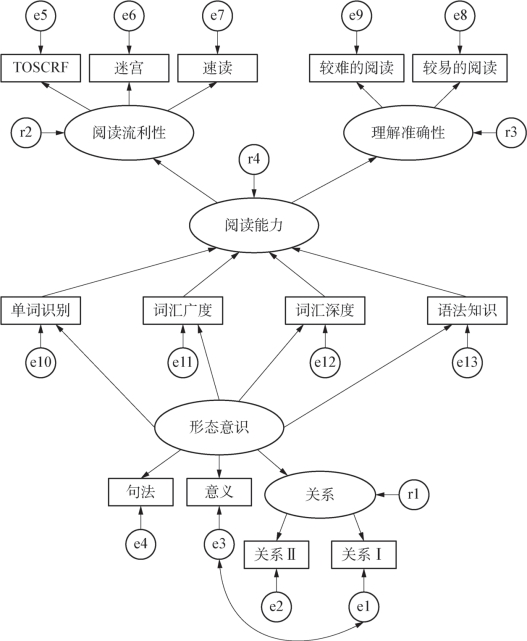
图5-11 假设的模型四
经过辨识、评估和修正,最终的模型如图5-12所示:
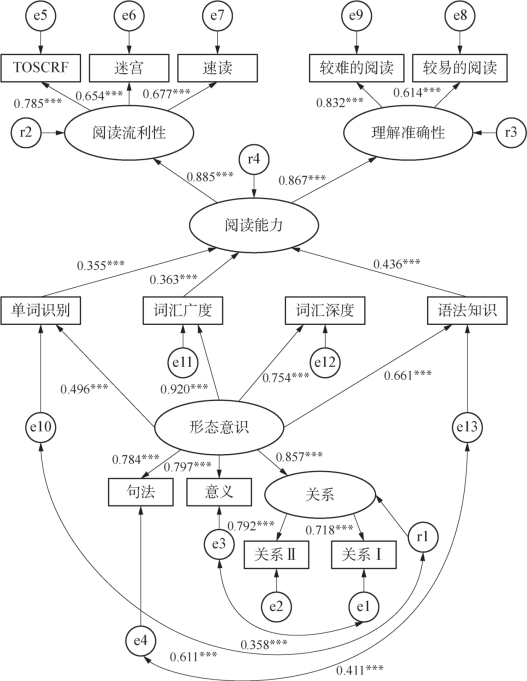
图5-12 修正后的模型四
***:p≤0.001
因为图5-12中的模型(包括测量模型和结构模型)与图5-8中模型的具体构建过程基本相同,在此不再赘述。对修正后的模型四进行评估,结果如表5-8所示。表中最右一列是图5-8所示模型三的评估结果,用于两个模型的比较。
表5-8 修正后模型四的评估结果及其与修正后模型三的比较
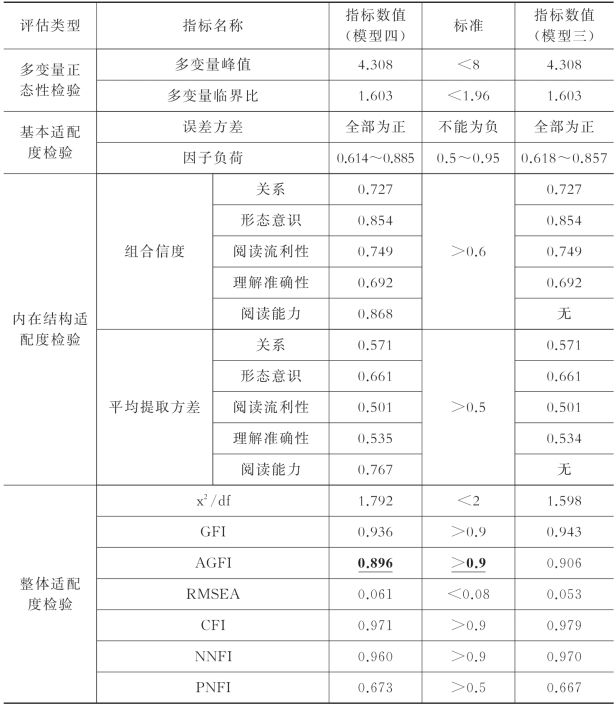
如表5-8所示,模型三和模型四在多变量正态性检验、基本适配度检验和内在结构适配度检验三个方面基本一致。这一方面是因为两个模型使用了相同的样本数据,另一方面是因为它们的整体结构高度相似。在组合信度和平均提取方差两项指标上,新增设的阅读能力变量表现很好:0.868的构念信度说明阅读流利性和理解准确性间的内在关联程度较高,0.767的平均提取方差说明阅读能力可以解释阅读流利性和理解准确性76.7%的方差,或者说,阅读流利性和理解准确性能够有效地反映阅读能力。但是在整体适配度方面,模型三明显优于模型四。并且,模型四的AGFI数值没有通过检验。然而,尽管如此,笔者认为模型四是可以接受的。专家(温忠麟等,2012;吴明隆,2010)指出,因为关于不同指标的优劣比较和指标数值的临界标准,目前仍有极大争议,所以在判断模型的整体适配度时需要慎重,最好综合考虑多个指标的表现。在表5-8中,模型四没有达到AGFI的指标要求,但是处于临界状态,距离0.9的标准极其接近。并且,模型四的绝对适配度指标ECVI(expected crossvalidation index,期望复核效度指数)、增值适配度指标NFI(normed fit index,标准化拟合指数)、RFI(relative fit index,相对拟合指数)和IFI(incremental fit index,增值拟合指数)、以及简约适配度指标AIC(Akaike's Information Criterion,赤池信息准则)、CAIC(Consistent Akaike's Information Criterion,一致赤池信息准则)和PGFI(parsimony goodness-of-fit index,简约拟合指数)等都通过了检验。
在图5-12中,形态意识通过单词识别、词汇广度和语法知识间接地影响阅读能力。那么,在控制这三个中介变量后,形态意识是否直接地、独立地影响阅读能力呢?为了回答这个问题,需要在图5-8中增加一条从“形态意识”指向“阅读能力”的单箭头路径。模型辨识的结果显示:新路径的出现导致词汇广度对阅读能力的影响由显著(β=0.363,p<0.001)转为不显著(β=0.077,p=0.68),单词识别和语法知识对阅读能力的影响也分别由β=0.355(p<0.001)和β=0.436(p<0.001)降为β=0.327(p<0.001)和β=0.375(p<0.001),同时新路径本身的回归系数在统计上不具有显著意义(β=0.366,p=0.104)。如果删除从词汇广度到阅读能力这条路径,那么结果如图5-13所示,从形态意识到阅读能力这条路径由不显著转为显著(β=0.452,p<0.001)。
对图5-13进行模型评估,然后比较它与图5-12的评估结果,笔者发现两个模型的适配度差别极小,可以忽略不计。也就是说,从统计上讲,两个模型都可以接受。但是因为两个模型的适配度差别不大,所以图5-13中形态意识对阅读能力的直接影响实际上等价于图5-12中被删除的以词汇广度为中介的间接影响再加上被削弱的以单词识别和语法知识为中介的间接影响。因此,从理论上讲,图5-12更好地反映了形态意识影响阅读能力的内部机制。综上所述,图5-12优于图5-13,说明在考虑了单词识别、词汇广度和语法知识的中介效应之后,形态意识对阅读能力没有直接和独立的影响。
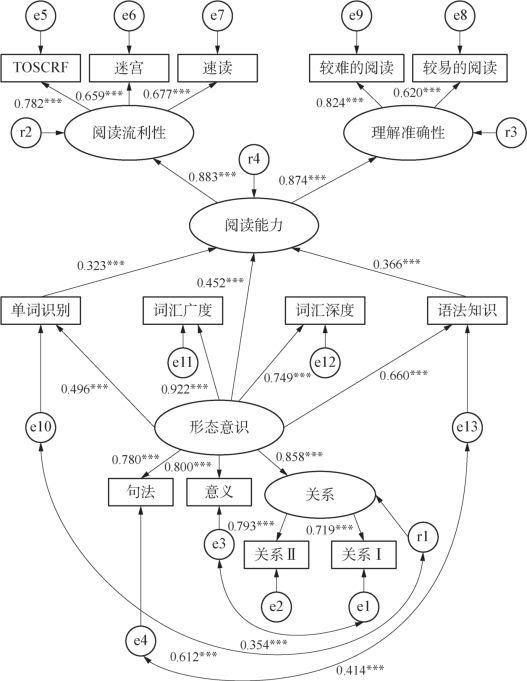
图5-13 模型四的检验模型
***:p≤0.001
根据图5-12中标示的路径系数,可以得知形态意识对阅读能力的间接效应分别是:
●形态意识→单词识别→阅读能力:0.496×0.355=0.176;
●形态意识→词汇广度→阅读能力:0.920×0.363=0.334;
●形态意识→语法知识→阅读能力:0.661×0.436=0.288。
形态意识对阅读能力的总效应是:
0.176+0.334+0.288=0.798[8]
根据AMOS输出结果中的多元相关系数平方报表,单词识别、词汇广度和语法知识可以联合解释阅读能力86%的方差,说明5-12中的模型包含了影响阅读能力的主要变量。
根据AMOS输出报表中的隐含相关系数(implied correlations)矩阵,形态意识、单词识别、词汇广度、词汇深度和语法知识与阅读能力的相关系数都在0.001水平上具有显著意义,具体数值分别是0.799、0.664、0.790、0.602和0.774。
