一、振 动
一个物理量(如交流电压、钟摆的位移等)在所观察时间内不停地经过最大值和最小值而变化总称为振荡。振动往往特指一个机械系统中某物理量的振荡(振荡是一般术语,振动只用于机械系统,包括声学系统)。振动的表现形式为系统中的物体沿直线或曲线经过其平衡位置附近来回重复地运动,称为机械振动。
力作用于物体,可产生直线加速运动,也可能产生机械振动。究竟产生哪种运动形式,取决于物体的惯性、弹性和摩擦力。机械振动是由物体受力产生形变后因弹性而产生的回复力以及由物体的质量所决定的惯性共同作用的结果。摩擦力则对抗物体的运动,决定了物体是否能产生运动及运动是否能保持。
最简单的振动形式是简谐振动。简谐振动的一个经典例子就是弹簧振子的振动。如图1-1所示,球在位置O时,弹簧为初始长度,作用于球上的弹力为零,这个位置是物体的平衡位置。如果把球拉到位置A后再放开,它就要在平衡位置O的左右(A←O→B)振动。
(一)简谐振动
小球为什么会振动呢?我们把它分为四个阶段来讨论。
第1阶段是从A到O。把球拉到A时,弹簧因拉长而产生了弹力(回复力),但这时弹力与手拉球的力量抵消,所以球不动。手一松开,弹力立即起作用,此时弹性势能最大,但速度尚为零,所以动能等于零。弹力使球向左方运动。此阶段弹力方向和运动方向都向左,球作加速运动(动能增加);弹力逐渐减小(势能减小)。当回到O点时,速度最大(动能最大),弹力为零(势能等于零)。
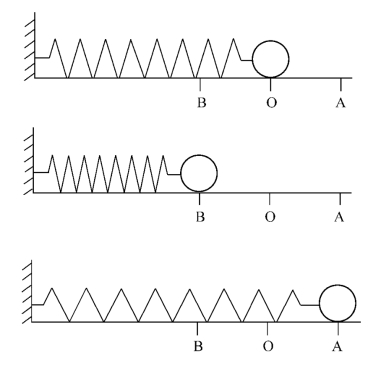
图1-1 弹簧振子的振动
第2阶段是从O到B。球到O点时虽然弹力为零,但它具有最大的速度,当然不会停驻在这个位置,而要继续向左运动。向左运动必然使弹簧受压,产生弹力,阻止小球向左继续运动。在这个阶段中小球做减速运动,弹力逐渐增大(势能逐渐增加),速度逐渐减小(动能逐渐减小)。达到B点时速度降为零,不能再向左运动。此时弹性势能最大,而动能降为零。
第3阶段是从B到O。这阶段与第1阶段相似,这个机械系统中的能量又从势能转化成动能。弹性势能由最大变为零,动能由零变为最大。
第4阶段是从O到A。与第2阶段相似,弹性势能由最大变为零,动能由零变为最大。系统中的能量又再次从动能转化成势能。
这样小球就完成了一次振动,只要条件不变,球就会一直这样振动下去。
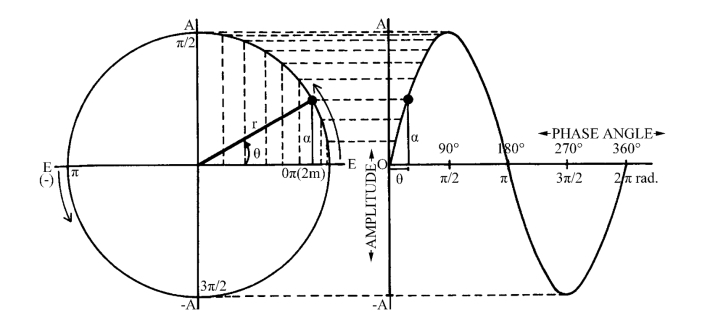
图1-2 简谐振动可由做匀速圆周运动的质点在其直径上的投影运动
简谐振动可由做匀速圆周运动的质点在其直径上的投影运动来等效(图1-2)。其中A为振幅,是振动物体离开平衡位置的最大位移。物体完成一个全振动(交替变化1次)所需的时间称为振动周期,用T表示。因为质点沿圆周运动1周(2π)所需的时间是T,所以圆周运动的角速度ω=2π/T。物体在单位时间(1s)内完成全振动的次数称为振动的频率,一般用f表示,单位以德国物理学家Hertz(赫兹)命名,简写为Hz。频率为周期的倒数,f=1/T=ω/2π;则ω=2πf。由于ω是f的2π倍,因此,又称为简谐振动的圆频率。
由图1-2可知,振子在任意时刻t的运动状态,可用量ωt+φ完全确定。ωt+φ是确定做简谐振动的物体的运动状态的物理量,称为相位或位相。由于相位用角度表示,故也称为相角。φ称为初相角。
简谐振动的位移、速度、加速度与时间的关系都符合正弦函数(它可由公式推导),只不过相位上存在差异。加速度超前速度90°,位移落后速度90°,加速度与位移反相(图1-3)。
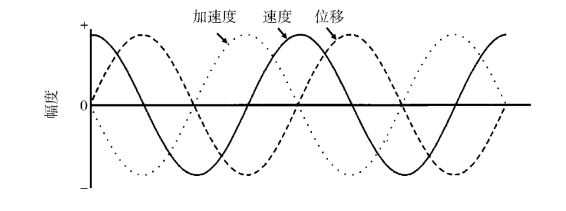
图1-3 位移、速度、加速度的相位关系
实线:速度;密虚线:超前位移90°;疏虚线:滞后加速度90°
(二)自由振动与阻尼振动
弹簧振子只要不受摩擦和其他任何阻力,小球就将保持一定的振幅永远振动下去。理想状态下,一个振动物体不受任何阻尼力的影响,在其回复力作用下所做的振动称为无阻尼自由振动。我们还发现,上例中的小球不论离开平衡位置多远,只要仍在弹簧的弹性限度之内,那么弹簧振子完成一次振动所花费的时间就是恒定的;单位时间内完成振动的次数(频率)也是恒定的。这是因为,物体做无阻尼自由振动时的频率是由振动系统内部的弹性和质量决定的,它们都是由系统本身的性质所决定的量,因而被称为固有频率。
实际上,由于摩擦和其他阻力无法避免,振动物体因克服摩擦和其他阻力做功,能量和振幅会逐渐减小,这种振动称为阻尼振动。能量减小主要有两种方式:一是由于摩擦阻力的存在,使振动能量逐渐转变为热能,称为摩擦阻尼;另一种是由于物体的振动引起邻近媒质质点的振动,使振动的能量逐渐向四周传播出去,转变为波动的能量,称为辐射阻尼。音叉的振动就是辐射阻尼的一个很好的例子。
当振动系统的阻尼较低时,振荡幅度缓慢下降;而当振动系统中的阻尼较高时,振荡形式很快终止。当阻尼高到连一次完整的振荡形式都无法完成时,该阻尼称为临界阻尼。
