二、波
下面我们要讨论振动体对周围弹性媒质的影响。以音叉振动产生的声波为例:音叉振动,使其周围的一部分空气媒质离开平衡位置,由于媒质具有的弹性,必然会在其附近产生使它回到平衡位置的弹性力,因而这部分媒质将在其平衡位置附近振动起来。与此同时,这部分媒质又将对其所在部位周围的媒质产生力的作用,振动就会传到它的周围各部。周围各部分的振动又使较远的各部分跟着振动,这样就会越传越远,传播到物体的全部。由此,可以给出波的定义:机械振动在弹性媒质中的传播过程所形成的机械波,下文简称为波。
(一)波的定义要点
(1)媒质质点只在平衡位置附近振动,传播的是凸起、凹下或密集、稀疏的状态,质点本身并不随波动而迁移。例如,往平静的水池中投一石子,以石子落下去的地方为中心,会出现凸、凹两种圆环交替传播到整个水池。如果在水面上漂有树叶,它并不随着波的传播而漂向远处,只是在原位置上下振动(严格讲,水波的这种性质与空气的振动是近似的)。铃铛振动时,击动附近的空气,使空气一会儿密集、一会儿稀疏,铃铛附近空气的密集和稀疏又产生弹性力,引起附近部分空气的振动。如此,在空气中密集状态和稀疏状态相间出现,并向远处传播,即形成声波。
(2)机械波不能脱离弹性媒质而独立存在。若把钟放在一个大玻璃罩中,我们仍可以清晰地听到钟的滴答响声。然而当我们通过罩子上的抽气孔往外抽气时,滴答声逐渐变弱;当罩内的空气被抽得十分稀薄时,钟声就几乎听不见了。
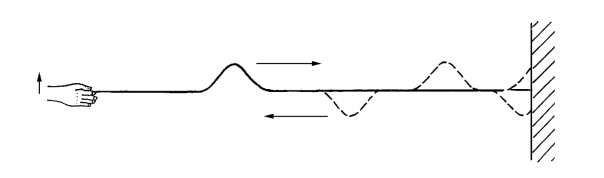
图1-4 横波波源
(3)波的传播伴随有能量的传递。一处质点振动引起周围质点振动,振动质点具有能量。因此,波的传播是伴随有能量的传递,即波是能量传递的一种形式。要想维持振动的传播,必须有提供能量的来源——波源。例如,一根绳子一端固定,另一端用手上下抖动一次,一个凸起和凹下的状态就通过绳子传到固定端。要使绳子持续出现凸起和凹下的状态,手就必须始终抖动。
(二)波的传播形式
1.横波 把1根橡皮绳的一端固定,手持另一端上下振荡1次,这样就在橡皮绳上先形成一个凸起的形态,然后又形成一个凹下去的状态。凸起的和凹下去的状态会通过整个橡皮绳传到另一端。这个过程中,绳子的每一段都在上下振动,而波沿水平方向传播。这种弹性媒质分子振动方向与波传播方向相垂直的波,称为横波(图1-4)。上述水面波类似于横波。
2.纵波 把1根较长弹簧的一端固定,另一端用手轻轻一推,就形成了一个弹簧圈较密的密部。由于弹簧各处弹力的作用,密部沿着弹簧一直向前传播;如用手轻轻一拉,就形成了一个弹簧圈较疏的疏部,由于弹簧各处弹力的作用,疏部也沿着弹簧一直向另一端传播。如果不断地推拉弹簧,就可以看到一系列的密部和疏部依次向前传播。这种媒质分子振动方向和波传播方向平行的波,称为纵波,好似疏、密相间的“麦浪”,也称为疏密波(图1-5)。
(三)波长、频率与波速

图1-5 声波的产生与传播
波的传播方向称为波线。同一波线上相邻的两个同相位的质点之间的距离,即一个完整波的长度,称为波长,用λ表示。波传过一个波长的时间,称为波的周期T。波速c是指一定的振动相位在空间的传播速度,即振动的任一相位在1s内前进的路程。由此可知,波速和波长及周期之间的关系是:
![]()
周期的倒数f=1/T,称为频率。波的频率是在单位时间内波动推进的距离中所包含的波长的数目。波速和波长及频率的关系是:
![]()
波速仅由弹性媒质的性质决定,不受波长、频率和振幅的影响。波的传播速度决定于媒质的密度和弹性模量。理论上可以证明,波速是由媒质的密度ρ和弹性模量k决定的。
(四)波的基本特征
1.反射、折射与散射 当声波自一种媒质入射到另一种媒质时,若它们的特性阻抗不同,就产生反射和折射(图1-6)。
(1)反射:波阵面由两种媒质之间的表面返回的过程,向表面的入射角等于反射角。反射定律:入射角等于反射角,即θi=θr。
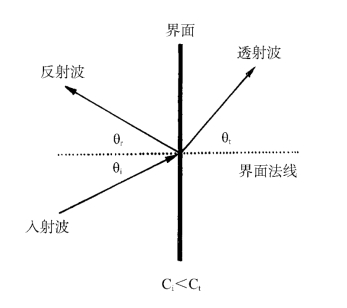
图1-6 波的反射与折射
(2)折射:因媒质中声速的空间变化而引起的声传播方向改变的过程。折射定律:入射角的正弦和折射角的正弦的比值等于两媒质中声速的比值(Ci和Ct分别为在两种媒质中的声速):
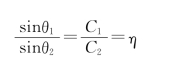
(3)全反射:指声波完全不传到第2媒质,而由分界处全部反射的现象(当入射角>临界角θk时,即发生全反射)。如果分开两种媒质的边界具有无限平面的形状,这种边界的反射称为镜反射,如同光的反射。一个人站在桥上,水中出现的桥和人影,即为光的全反射;这应区别于光的直射现象,如一个人或电线杆在太阳底下出现的人影,即为光的直射现象。
(4)散射:密度与弹性不同的障碍物所产生散射,即声波经许多方向不规则反射、折射或衍射的总称。
2.干涉与衍射
(1)干涉:即几个振动的叠加将产生干涉。由于干涉现象,声场中可产生驻波或定波(频率相同或相近的声波相加时所得的现象)。
(2)衍射:即声波绕过障碍物使传播方向改变的现象。波长对障碍物大小的比值越大,衍射也越大,如果障碍物的尺寸远>波长,虽然还有衍射,但在障碍物背后的边缘附近将形成一个没有声波的区域,叫声影区。
