三、频谱分析
上述是以“幅度与时间”的函数关系来描述信号随时间变化的过程,称为时域分析。但有时我们也关心构成声波的各频率成分的幅度,也就是信号的频率特征,可以由频域分析,即以“幅度与频率”的函数关系来描述信号的频率组成。
(一)复合波
纯音,除了由音叉或电子学正弦波发生器发出外,在现实生活中是不常见的。大多数声音都有若干强度不同的频率成分,它们在特定的相位关系下复合组成在一起。若合成波能每隔一定的时间间隔重复自身的波形,则称为周期性波;否则,则称为非周期性波。
简谐振动产生单一频率的正弦波,当该振动在媒质中传播时,声波具有单一频率,称为纯音。当两个或多个振动方向、传播方向相同的纯音叠加在一起的时候,就构成了复合波。
1.波的合成 若两个波的频率相同,其合成波仍是正弦波,合振幅决定于分振动的相位关系(图1-13)。若两个波频率不同,其合成波的情况较为复杂(图1-14)。
如两个分振动的振幅均为A,f1和f2较高,且较为接近(如1 000Hz和1 003Hz),则会出现一种称为拍(beat)的振动形式:合振动的频率等于f1和f2的平均值;合振动的振幅在0到A之间以f2-f1(假定f2>f1)的频率呈现周期性的变化。这两个分振动的频率之差f2-f1称为拍频(图1-15)。
2.周期性复合波 当两个或有限多个正弦波合成在一起时,合成波的振幅完全由各波在每一时刻的数值的累加决定,最终的波形虽然不再是正弦波,但仍表现出周期性的特点。以图1-14为例,三个不同频率的正弦波f1、f2、f3(频率分别为1 000Hz、2 000 Hz、3 000Hz)。下面的三个波形分别对应f1+f2、f2+f3、f1+f2+f3的合成波,它们仍每间隔一段时间重复自己的波形。值得一提的是,合成波的周期仍与f1的周期相同,在下文的基频与谐波中将予说明。
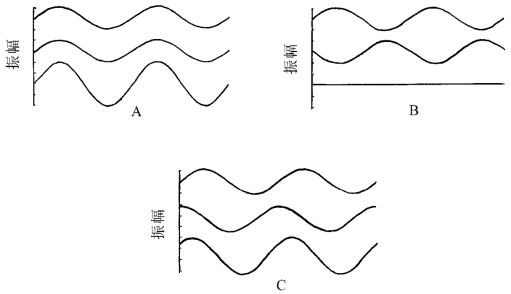
图1-13 频率相同的正弦波的合成
A.两个相位相同的正弦波的合成;B.两个相位相反的正弦波的合成;C.相位差90°的两个正弦波的合成
(摘自Essentials of Audiology,p18.figure 1-10)
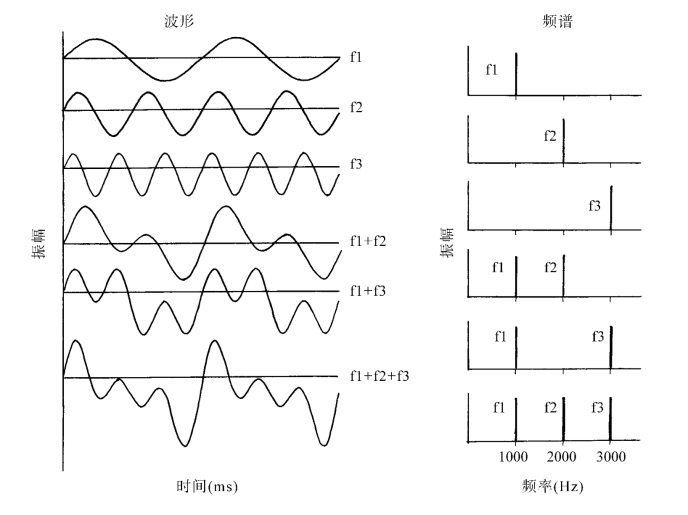
图1-14 频率不同的波的合成
(摘自Essentials of Audiology,p19.figure 1-11)
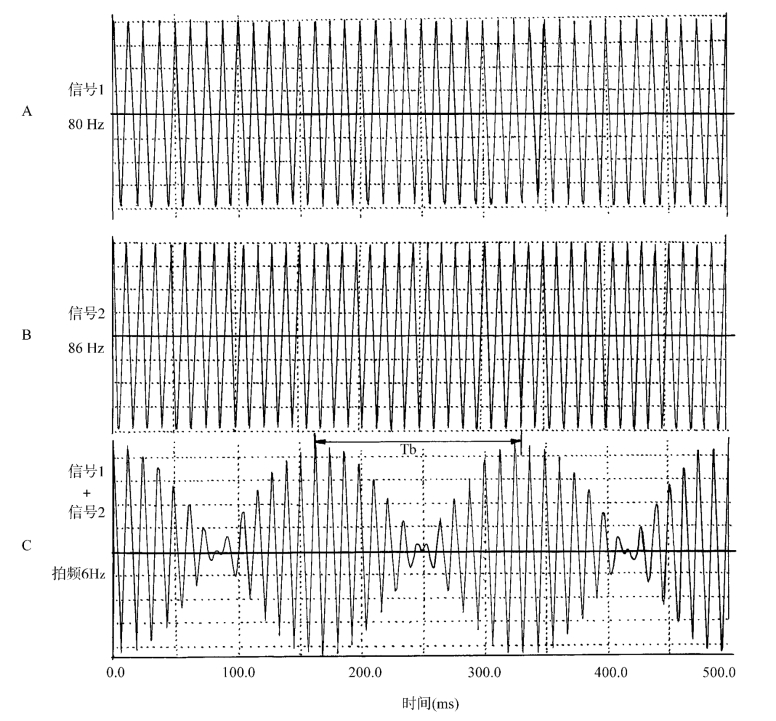
图1-15 信号1(80Hz)(A)和信号2(86Hz)(B)的合振动波形(C),合振动振幅波动周期为Tb,约为166.7 ms,相当于6Hz。即拍频为6Hz
3.非周期性波 非周期性波不能由多个正弦波合成,在时域波形上也不表现出周期性。瞬态噪声或随机噪声都为非周期性波。
(二)频谱分析
1.傅立叶分析 法国数学家傅立叶(Fourier)首先提出,任何周期性函数都可以分解成几个直至无限个正弦函数之和,称为傅立叶级数(图1-16)。该信号的周期所对应的频率f0,是各正弦信号中频率最低的,其余各正弦信号的频率均为f0的整数倍。因此f0称为基频,2f0所对应的正弦信号称为一次谐波,3f0所对应的正弦信号称为二次谐波……以此类推。
2.复合声的频谱 运用傅立叶级数的原理,我们把周期性的时域函数的幅值和相位分量表示为频率的函数(频域)。借用于光谱(红、橙、黄、绿、蓝、靛、紫)的含义,其分布图形称为频谱,称为傅立叶变换。以频域表达信号时,二维直角坐标的横坐标轴代表频率,纵坐标轴表示信号幅度的有效值,它反映了各频率成分对总体功率的贡献大小。周期性变化的信号,各频率成分是离散的,间隔为f0,频谱为线状谱;谱线只出现在基频的整数倍的频率上;谱线高度的总体趋势是随着谐波次数的增高而逐渐减小的。所以周期性信号的频谱表现出离散性、谐波性、收敛性三个特点。对于只有单一频率的余弦信号,其频谱只为一根谱线,称为纯音;而对于由若干个余弦信号构成的周期性信号,如乐音、嗓音等,频谱为几根谱线,称为周期性复合音。
日常所面临的大多数声音是非周期性信号,是不符合傅立叶级数展开条件的。不过由上面的讨论可知,非周期性信号可视为一个周期无限大的周期性信号,这样基频频率就无限小,信号频谱相邻谱线间的间隔也无限小,谱线无限密集,离散频谱就变成连续频谱,包含了从零到无穷大之间的一切频率。
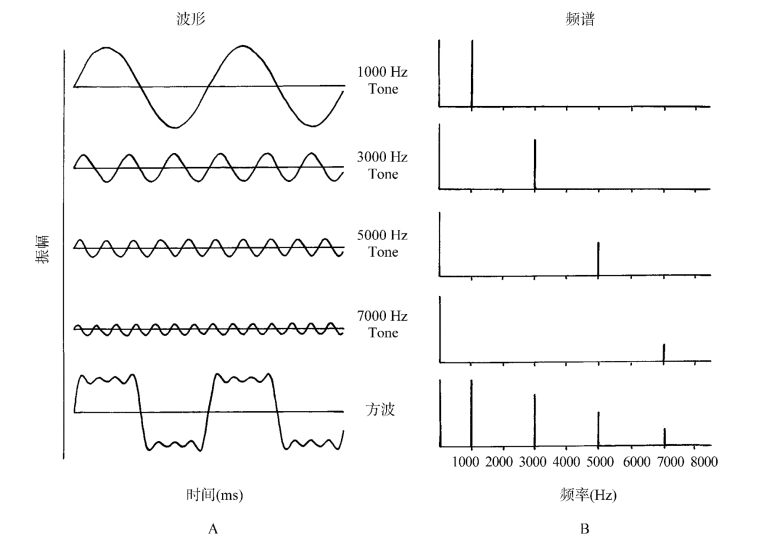
图1-16 周期性方波信号由各次谐波合成
A.频率不同的正弦波,最下方为合成的方波;B.各波对应的频谱
(三)倍频程刻度
声学测量的另一个重要方面是对频率的量度。频率计量一般很少采用线性刻度,而多采用对数刻度,这与心理声学中人对音调的主观感受是一致的。另外在对数坐标上,人耳最敏感的频率1 000Hz也恰巧位于人听觉频率范围(20~20 000Hz)的中部。如同声音的强度以分贝计量,对频率的计量我们一般采用倍频程(octave):频率每增加一倍,称为一个倍频程,在音乐上对应一个八度音阶变化。
从听力学角度讲,频率跨度间的上下限频率之比等于2的多少次幂,该频率范围就有多少个倍频程。如频率从f至2f为1个倍频程;从f至4f为2个倍频程;从f至21/3f为1/2个倍频程。
(四)滤波器
通过频谱分析了解了信号的频率组成,我们也可以通过各种不同频率响应的滤波器(filter)来对信号进行频谱处理,将不需要的频率成分滤除。滤波器按其频率响应(简称频响)可分为高通滤波器、低通滤波器和带通滤波器(图1-17)。高通滤波器只允许某一频率以上的高频信号无衰减地通过滤波器;低通滤波器只允许某一频率以下的低频信号无衰减地通过滤波器。将高通和低通滤波器组合可以形成带通或带阻滤波器。
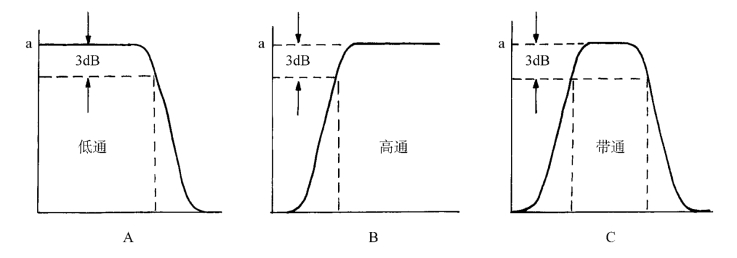
图1-17 滤波器的截止频率和滤波斜率
在声学测量中最常用的是带通滤波器。其主要参数包括中心频率、带宽和波形因数Q。带通滤波器可以看作是由高通和低通滤波器串联的结果。低通和高通滤波器的截止频率可作为通带的上限截止频率f2和下限截止频率f1,两者之差就是滤波器的带宽。
在分析噪声的频谱特征或主要频率成分时,常以一组带通滤波器将整个音频范围划分成若干个通带。通带的划分可以采用等带宽、等百分比、等比带宽等几种形式。由于通带的不同划分,中心频率的计算也是不同的。
等带宽滤波器是指在任何频段上滤波通带的频率跨度都是固定的,其中心频率是上、下限截止频率的算术平均值,即:
fc=(f1+f2)/2
等百分比带宽滤波器的中心频率是预先设定的,带宽是中心频率乘以某一固定的百分比,所以它的频带宽度随滤波通带的中心频率升高而增加。
等比带宽滤波器是指滤波器的上、下限截止频率之比为一个固定的常数,其中心频率是上、下限截止频率的几何平均值,即:
![]()
当等比带宽滤波器上下限截止频率的比值为2或2的1/2幂、1/3幂时,f2是f1的倍频程或1/2个、1/3个倍频程,所以这些滤波器就分别称为倍频程、1/2倍频程、1/3倍频程滤波器。
对于倍频程滤波器,f2=2f1,代入上式中,得f1=2-1/2fc,f2=21/2fc;
对于1/2倍频程滤波器,f2=21/2f1,得f1=2-1/4fc,f2=21/4fc;若中心频率fc=1 000 Hz,则f1=707Hz,f2=1414Hz。
对于1/3倍频程滤波器,f2=21/3f1,得f1=2-1/6fc,f2=21/6fc;若中心频率fc=1 000 Hz,则f1=890Hz,f2=1122Hz。
对整个音频范围进行等比(倍频程)通带的划分时,有一套经国际标准化的标称值。对于1/3倍频程滤波器而言,它们是16,20,25,31.5,40,50,63,80,100,125,160,200,250,315,400,500,630,800,1 000,1 250,1 600,2 000,2 500,3 150,4 000,5 000,6 300,8 000,10 000,12 500,16 000Hz。
波形因数Q是描述滤波器频率选择性的参数,定义为滤波器在衰减为60dB时的带宽与其半功率点(-3dB)的带宽的比值。
(五)噪声
噪声的定义含心理学和物理学两层意思。从主观感受的角度来看,所有不希望的干扰声统称为噪声。即使是优美的音乐,如果它干扰人们的睡眠或思考,也可认为是噪声。从物理学的角度看,一切不规则的或随机的声信号都称为噪声。在声学和听力科学中,噪声的定义更偏向于后者。
1.白噪声与粉红噪声
(1)白噪声(white noise):是听觉研究中十分有用的一类噪声。如同光学中包含了各种颜色的光是白光一样,白噪声的含义表明在较宽的频率范围(20~20kHz)内,各等带宽的频带所含噪声能量相等的频率,即各频率的能量连续均匀分布。
(2)粉红噪声:指在较宽的频率范围内,在各等比带宽的频带上测量时,频谱连续且均匀但按倍频程增加而递减的噪声;若采用等带宽的滤波通带,以对数分布的频率刻度为横坐标,这时粉红噪声的频谱包络为每倍频程下降3dB的斜线,低频成分能量较多。在光学中红光的频率较低,从白光的光谱中滤掉一些高频成分光线即成粉红色。借用光学中的这一现象我们将上述噪声称为粉红噪声。
2.窄带噪声 具有连续谱和恒定功率谱密度的白噪声,经过带通滤波器滤波后,就成为带通噪声,根据带宽的不同可分成宽带噪声和窄带噪声。滤波器有倍频程、1/2倍频程、1/3倍频程滤波器等。
如果把一个宽带噪声分成许多窄带,则宽带噪声的总能量可由各窄带噪声的能量相加而得到。单位带宽1Hz内的声强称为谱能级(spectrum level)Lpf。若某白噪声的频谱宽度为100~10 100Hz(BW=10 000 Hz),总能量为I,强度LWN=10lgI=70dB SPL。白噪声的带宽BW为10 000Hz,表明它由10 000个等能量的通带组成。因此,由定义应有:
Lpf=10log(I/BW)=10lgI-10lgBW=70dB SPL-10lg 10 000=30dB SPL。
可求得单位频率所携带能量Lpf=30dB SPL。若该白噪声经中心频率为1 000Hz的倍频程滤波器滤波后,其带宽为707Hz,则其能量为Lpf+10lgBW=30+10lg707=58.5 dB SPL。
3.言语噪声(speech noise) 是对白噪声进行特殊的滤波处理后获得的噪声信号,其频谱范围与言语相似。在临床上常常用来作掩蔽言语信号。言语噪声在100~1 000 Hz间为等能量,而在1 000~6 000Hz间每倍频程递减12dB。根据对言语频谱的测量,言语噪声的频谱特征适合用于掩蔽言语信号。Byrnes等在1994年测量了包括普通话和广东话在内的12种语音的长时程平均言语频谱(long-term average speech spectrum,LTASS),发现尽管男女声之间存在一定差别,但是12种语音的LTASS非常相似,有明显的带通特性,如其高通截止频率约为200Hz,低通截止频率约为500Hz.,200Hz以下每倍频程递减约20dB,500Hz以上每倍频程递减4dB。
4.脉冲噪声(impulse noise) 是指持续时间短促的噪声。枪、炮等武器发射、爆炸和工业中的气锤、冲床等发出的声音都属于脉冲声。通常把峰值压强超过177dB SPL、持续时间较长的脉冲信号称作冲击波或压力波。
(六)信噪比
在一个发生、检查、测量或记录声学信号的电声学系统中,与信号存在与否无关的一切干扰,称为背景噪声。一般的噪声概念可以为紊乱、断续或统计上随机的振荡(可引申为在一定频段中任何不需要的干扰,如电波干扰,称为“电噪声”)或振动(不需要的声音,称为“声噪声”)。信号强度与噪声强度之比,称为信号-噪声比(signal-to-noise ratio,SNR),简称为信噪比。换算成dB表示,则为信号声级与噪声声级之差。
临床听力学研究中,特别是有关噪声下的言语识别以及声源定位能力等的研究中,有时会人为模拟某种环境噪声:如交通噪声、餐馆噪声、多人交谈等。在怎样的信噪比条件下,患者能够正确识别语义或方位,往往是研究者最关心的问题。
