2.1 本课重点内容提示
1.数列收敛的判别方法.
（1）用ε−N语言证明数列的极限（用于已知极限值数列的证明）.
（2）夹挤定理：
设数列{xn}，{yn}，{zn}，存在N，对于任意的n＞N，有
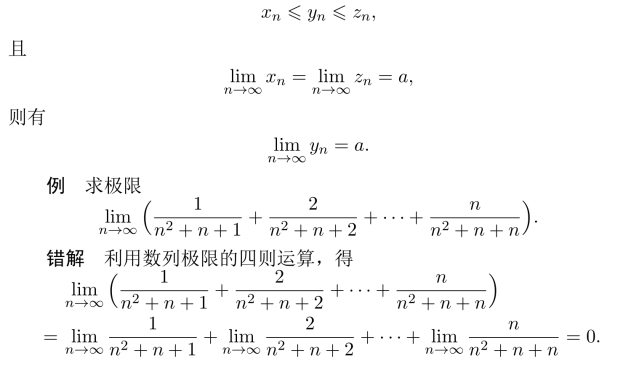
这种解法是错误的，因为数列极限的四则运算中的求和是有限多个，而不是无穷多个，所以不能利用之.
解 注意到
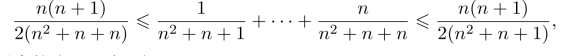
利用夹挤定理，得到
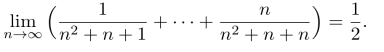
（3）单调有界数列必收敛.
对于数列的通项具有递推关系的数列，例如
，可以分别验证数列通项的单调性和有界性，利用单调有界数列必收敛准则，证明数列是收敛的.
（4）柯西（Cauchy）收敛原理证明数列收敛（掌握正反两方面的分析表达）.
数列满足Cauchy收敛原理的分析定义：
数列{xn}收敛⇔∀ε＞0，存在正整数N，对于任意的自然数m，n＞N，有
|xm−xn|＜ε.
数列不满足Cauchy收敛原理的分析定义：
数列{xn}不收敛⇔存在ε0＞0，对于任意的正整数N，总存在两项xm，xn（m，n＞N），使得
|xm−xn|≥ε0.
或者，存在某个ε0＞0，不会有这样的正整数N，使当任何自然数m，n＞N时，都有
|xm−xn|＜ε0.
2.上（下）确界的定义及确界唯一性定理（了解）.
3.收敛数列的性质.
（1）唯一性.收敛数列的极限值是唯一的.
（2）有界性.若数列{xn}极限存在，则该数列有界.
注 有界数列不一定收敛，但是单调有界数列一定收敛.
（3）保序性.若两个数列的极限值有序，则从某一项起，两个数列的项保持相同的序：
设
且a＞b，则存在正整数N，∀n＞N，有xn＞yn.
应当注意的是，反之不然，例如，
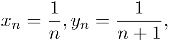
但是
但是，下述结论成立：
设数列{xn}，{yn}，如果存在正整数N，∀n＞N，有xn＞yn，则有
读者可自己证明该结论.（4）若数列{xn}收敛，则其任何子数列{xkn}与{xn}有相同的极限.
利用其逆否命题，可以判断数列{xn}不收敛.即如果数列{xn}的任意两个子列不收敛，或者收敛到不同的极限值，则{xn}不收敛.例如由此可以证明数列{cosnπ}不收敛.但是下面的结论成立.
例
的充分必要条件是
其证明见本课拓展习题讲解的例.