13.1 本课重点内容提示
2026年01月14日
13.1 本课重点内容提示
1.渐近线.
渐近线描述的是曲线上的点沿曲线趋于无穷远时,该点与一条固定直线的距离趋于零,即曲线的渐近性态.根据渐近线的斜率,可分为垂直渐近线、斜渐近线和水平渐近线.
(1)垂直渐近线
若
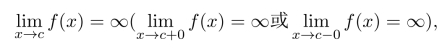
则称x=c为f(x)的垂直渐近线.
(2)斜渐近线(包括水平渐近线)
设渐近线为y=ax+b,则
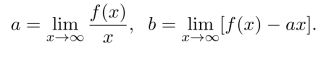 (https://www.daowen.com)
(https://www.daowen.com)
2.根据函数的性态(包括函数的定义域、对称性、周期性、单调性、凸凹性、拐点、极值、渐近线等性态)进行作图.
具体来说,利用一阶导数确定函数的增减性、函数的驻点,利用二阶导数确定函数的凸凹性、极值和拐点,再求出函数的渐近线,这样利用代数这一工具详细地刻画了函数的基本性质,也为函数的图形的描绘提供了较为准确的信息.
3.曲率描述了曲线的弯曲程度,计算曲线的曲率,在实际生产中有很广泛的应用.
设曲线C的方程为y=f(x),且f(x)有连续的二阶导数,则曲率
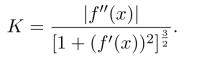
对于参数方程x=x(t),y=y(t),t∈[a,b],且x(t),y(t)在定义域上有连续的二阶导数,则曲率
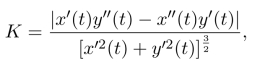
曲率半径![]()
4.了解弦位法和牛顿法求方程的近似解.
