16.3　课外练习

16.3　课外练习

A组

B组

习题16.4　求数列的极限

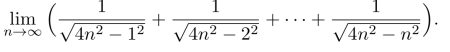
习题16.5　利用定积分的定义求数列的极限

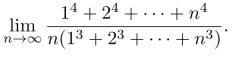
习题16.6　设f（x）在[0，1]上可微，且满足条件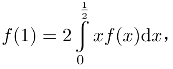试证明：存在ξ∈（0，1），使f（ξ）+ξf′（ξ）=0.

习题16.7　设函数f（x）在闭区间[a，b]上具有二阶导数，且

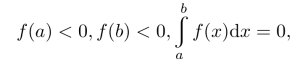
证明：存在一点ξ∈（a，b），使得

C组

习题16.8　设正值函数f（x）在闭区间[a，b]上连续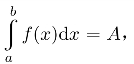，证明：

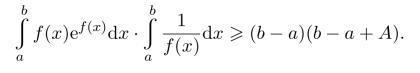
习题16.9　设函数f（x）为定义在（−∞，+∞）上，以T＞0为周期的连续函数，且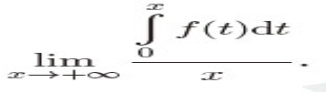

习题16.10　设函数f（x）连续，

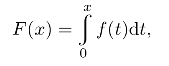
证明F（x）可导，且

习题16.11　设函数f（x）在闭区间[a，b]上连续，在开区间（a，b）内可导，且有

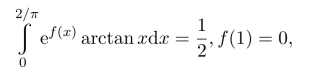
则至少存在一点ξ∈（0，1），使得