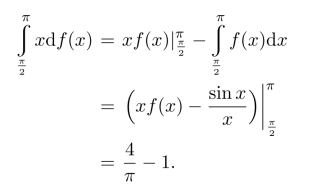17.2　精讲例题与分析

17.2　精讲例题与分析

17.2.1　基本习题讲解

17.2.2　拓展习题讲解

例17.6　求变上限定积分的导数或极限.

其中第二步利用了积分中值定理，因为f（x）连续，不能再利用L’Hospital法则了.

注　其实，上面的推导并不严密.应该利用f（0）≠0及连续性，得到0点一个邻域，在此邻域中再利用中值定理，就比较好了.请读者想想为什么.

证毕.

方法二，对于定积分的不等式的证明，可以构造相应的含参变量的定积分，利用其导数的性质得到结果，这种方法在有关定积分的不等式证明中比较有效.

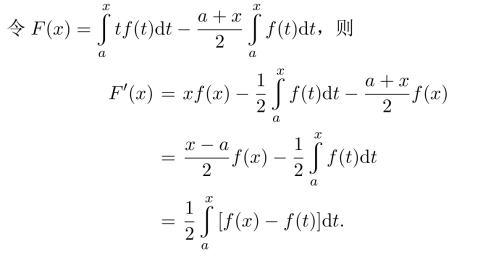
由f（x）在[a，b]上单增，得到F′（x）≥0，从而F（b）≥F（a）=0，得证.

类似的练习留给读者.

设f（x）在[a，b]上可微，且0＜f′（x）≤1，f（a）=0.试证：

(https://www.daowen.com)

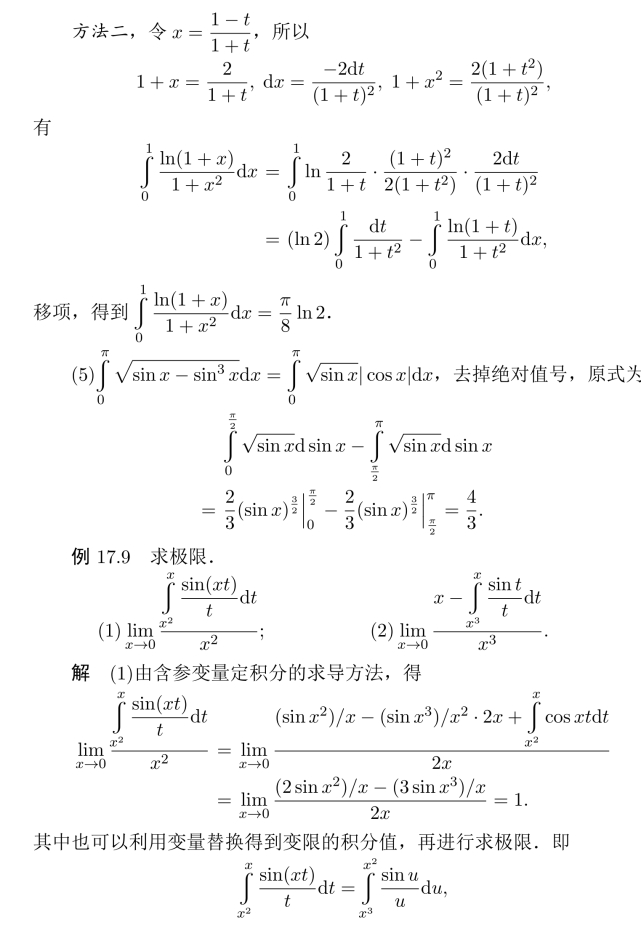
再利用L’Hospital法则，可得到同样的结果.

（2）同（1），得

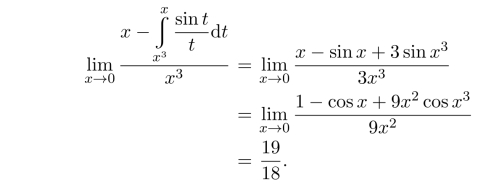
例17.10　f（x）有连续导数，且f（1）=0，求极限值

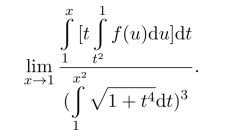
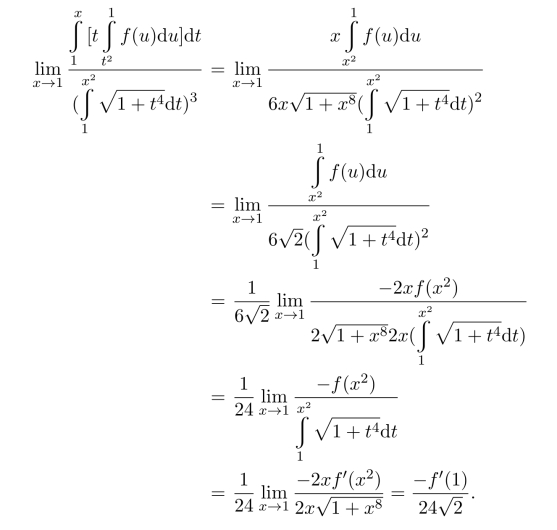
解　利用L’Hospital法则，

例17.11　证明：

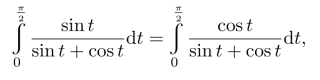
并求其值.

证明　令u=π/2−t，做此代换，则有

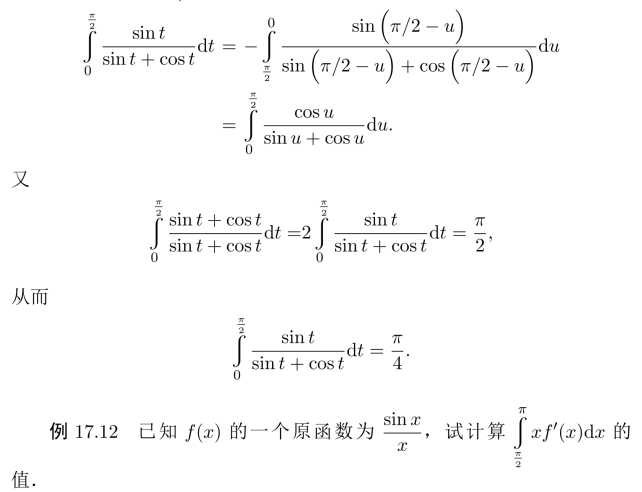
解　由原函数的定义，知

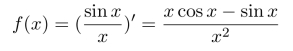
利用分部积分，得