4.2　精讲例题与分析

4.2　精讲例题与分析

4.2.1　基本习题讲解

例4.1　求下列函数的极限.

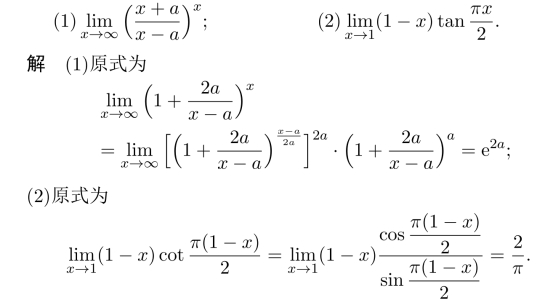
例4.2　说明tanx−sinx和sinx当x→0时，两个无穷小量的关系.

解　由于

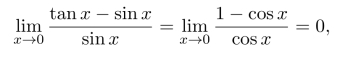
故前者为后者的高阶无穷小量.

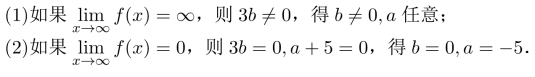
4.2.2　拓展习题讲解

例4.4　利用Cauchy收敛原理叙述f（x）在+∞处极限存在.

解　∀ε＞0，都存在X＞0，使得当任意两点x＞X，x′＞X时，就有(https://www.daowen.com)

例4.5　证明：

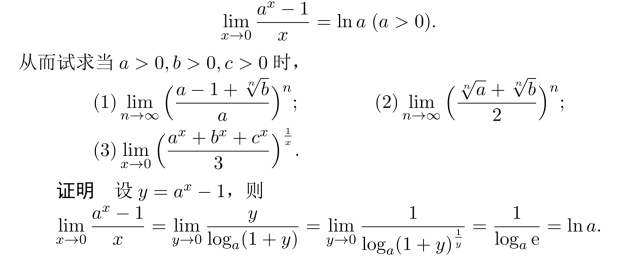
利用Heine定理，可知（1）、（2）中的数列的极限可以看做是相应的函数的极限，如果对应的函数的极限存在，则数列的极限也存在，且为同一极限.这种求极限的方法就是“利用函数的极限求数列的极限”，而基础是Heine定理.

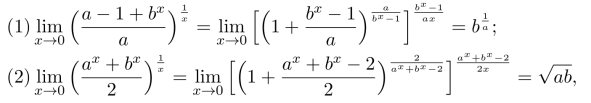
从而可得到前两小题的极限值.第三小题可类似求解，原式为

例4.6　求下列函数的极限：

例4.7　证明：y=sinx当x→+∞时极限不存在.

其中，两次利用了特殊函数的极限.