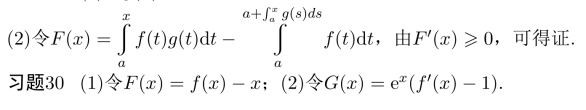附录E 课外练习答案与提示
E.1 第一课答案
（2）xn不以a为极限；存在ε0＞0，对于任意的正整数N，总存在一项xn（n＞N），使得
成立.
下面证明sinn不以任何实数A为极限.
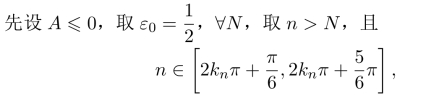
其中kn为正整数，依赖于n，但是
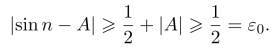
A＞0时的情形类似可以得到.故sinn不以任何实数A为极限.
习题1.7 注意到n！=n·（n−1）·（n−2）···1
即可.
习题1.8 当a＞0时，利用定义容易证明
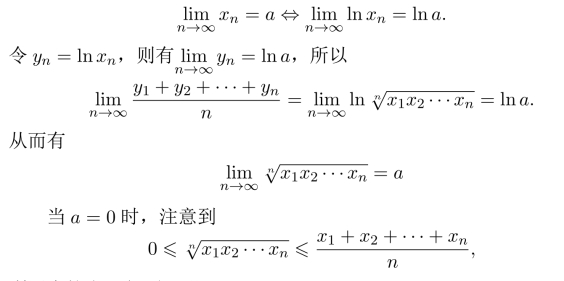
利用夹挤定理得到证明。
E.2 第二课答案
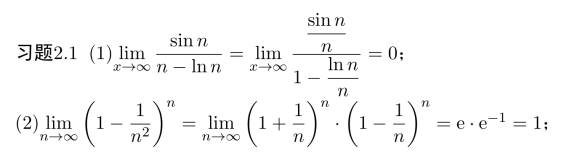
（3）注意到
则数列单调增加且有上界，故数列{xn}收敛，同习题2.3，可求得极限值为3.
习题2.5 由于
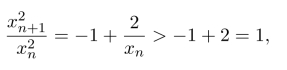
所以xn+1＞xn，数列{xn}单调增加且有上界.由单调有界定理，可知数列{xn}收敛.设极限为A，由
知2A2=2A，得到A=1，A=0（舍去）.
习题2.6 x1＞3，x2=4＞3，可以归纳证明，得xn＞3，故
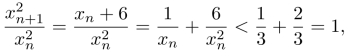
所以xn+1＜xn，xn单调减少且有界，知数列{xn}收敛且极限为3.
方法二，由极限ε−N定义亦可得到，证明从略.
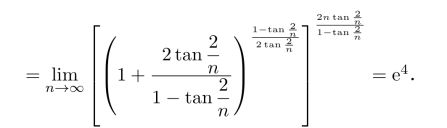
习题2.12 令yn=|x2−x1|+···+|xn−xn−1|，则数列{yn}单调增加且有界，故{yn}收敛，由Cauchy收敛原理，对于∀ε＞0，存在N，当m＞n＞N时，
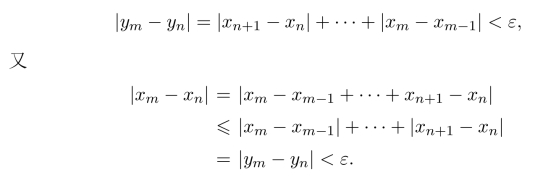
故由Cauchy收敛原理，得知数列{xn}收敛.
习题2.13 （2）、（3）、（5）在基本习题中已讲解；（1）较简单，不再给出证明；（4）的证明需用到区间套定理，将在第三课中给出证明.
E.3 第三课答案
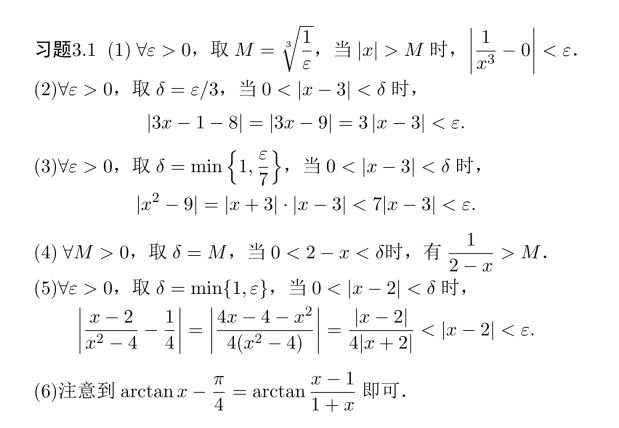
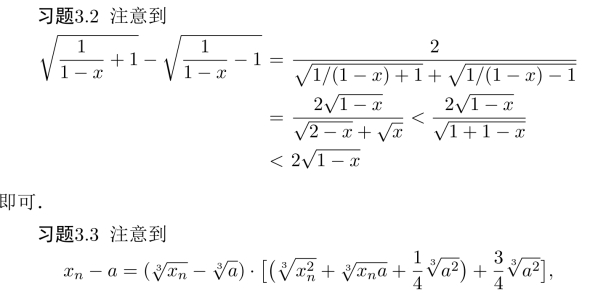
即可得到证明.
习题3.4 ∀ε＞0，取δ=amin{（eε−1），（1−e−ε）}，当0＜|x−a|＜δ时，有
可同理证明.
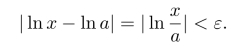
习题3.5 利用左右极限求得，极限值为1.
习题3.6 对于任意实数x0，当选取不同的数列（有理数数列、无理数数列）逼近x0时，极限值不同，故
不存在。
习题3.7 证明致密性定理：有界数列{xn}必有收敛子列.
证明：设数列{xn}有界，则存在a，b，使得对于任意的自然数n，有a≤xn≤b，将[a，b]二等分，其中至少有一个区间包含有数列{xn}的无限多项，记为[a1，b1]，再将[a1，b1]二等分，将含有{xn}无限多项的区间记为[a2，b2]，···，得到一闭区间列，且
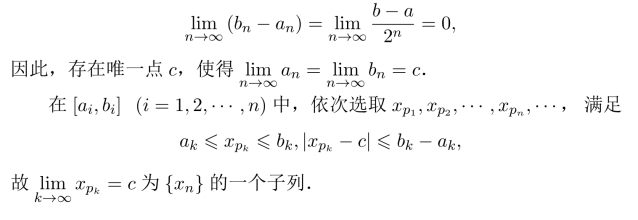
E.4 第四课答案
习题4.1 （1）原式为
注 本题也可以利用函数的极限的四则运算的结论来解.具体地，由原式得
得
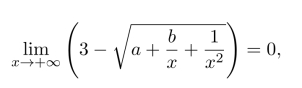
所以a=9，由
得b=−12.
习题4.5 答案为选项（D）.
习题4.6 答案从略.
习题4.7 a，b的值为a=1/5，b=7/5.
E.5 第五课答案
习题5.1 （1）原式为
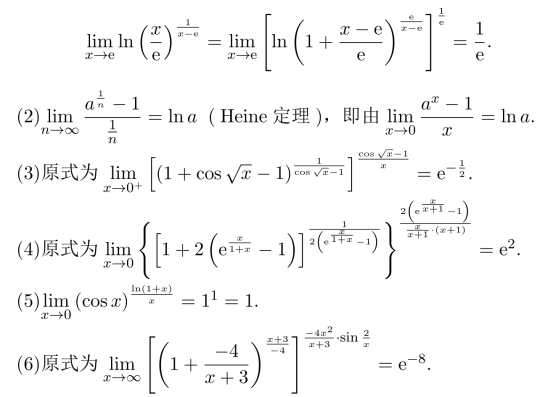
习题5.2 答案为
（1）第一类间断点；（2）第一类间断点；
（3）可去间断点；（4）连续.
习题5.3 x=0为可去间断点，x=2为第二类间断点.
习题5.4 由于
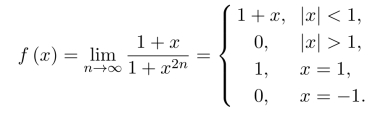
故函数f（x）于x=−1点连续，x=1点为第一类间断点，于其他点连续.
习题5.5 当α＞0，β=−1时连续；α＞0，β≠−1时为第一类间断点；α≤0时f（0+0）不存在，故为第二类间断点.
习题5.6 可由定义证明.
习题5.7 经过计算，得
同理可得x3，x4为可去间断点.
习题5.8 求极限得f（x）=
，x=0为可去间断点，x=kπ（k=±1，±2，···）为第二类间断点.
E.6 第六课答案
习题6.1 （1）先证明f（x）在（0，1]，[1，+∞）上为一致连续函数，再利用习题6.7的结论或者仿照习题6.7的证明得到本题的证明.同时从本题目还可以看出，区间I上的一致连续函数未必有界.
（2）由基本习题讲解中例6.3，取ε0=1，
类似地可以证明xsinx于（−∞，+∞）非一致连续.
习题6.2 由于f（x）于（0，1）内连续，且f（0）=−1＜0，f（1）=n≥1＞0，故存在x1∈（0，1），使得f（x1）=0，且当x＞1时，不可能有xn+nx−1=0，故正数解x1∈（0，1），设有两个解x1，x2，则
习题6.3 令F（x）=f（x）−g（x），在[a，b]上利用零点存在定理即可得到证明.
习题6.4 （1）函数f（x）在区间I上为一致连续，如果对于每一个ε＞0，存在δ＞0，使得当x′，x′′∈I且|x′−x′′|＜δ时，成立
（2）注意到下式，根据一致连续的定义很容易得到证明.
注 若没有“有界性”这一条件，结论还成立吗？
故极限值
习题6.6 如果f（x）≡0，x∈[a，+∞），则命题得证.
假设存在一点X1，且f（X1）＞0，则f（x）在[a，X1]上达到最大值，记最大值点为xX1，且f（xX1）＞0.
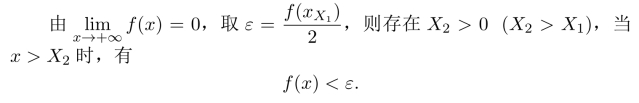
因此，f（x）在[a，+∞）上的最大值一定在[a，X2]上达到，命题得证.
f（x）于[a，+∞）上未必有最小值，例如f（x）=
x∈[1，+∞）便是反例.
习题6.7 由f（x）在区间（a，b]上一致连续，任意的ε＞0，存在δ1＞0，使得当任意的x′，x′′∈（a，b]且|x′−x′′|＜δ1时，成立
由f（x）在区间[b，c）上一致连续，对于上述的ε＞0，存在δ2＞0，使得当任意的x′，x′′∈[b，c）且|x′−x′′|＜δ2时，成立|f（x′）−f（x′′）|＜ε.
取δ=min（δ1，δ2），当x′，x′′∈（a，c）且|x′−x′′|＜δ时，不妨设x′≤x′′，若x′，x′′∈（a，b]或者x′，x′′∈[b，c）时，均有
若x′∈（a，b]，x′′∈[b，c）时，有
习题6.8 先证明充分条件，由于f（x）在（a，b）上连续，则存在f（a+0）和f（b−0），定义
f（x）于[a，b]上连续，故f（x）于[a，b]上一致连续，所以f（x）于（a，b）上一致连续.
再证必要条件，若f（x）在（a，b）内一致连续，即任意的ε＞0，存在δ＞0（δ＜b−a），使得当任意的x1，x2∈（a，b）且|x1−x2|＜δ时，有
将x1，x2取在（a，a+δ）内或在（b−δ，b）内，由Cauchy收敛准则知f（a+0），f（b−0）存在且有限.
E.7 综合训练一答案
习题1 （1）利用Stolz定理或者类似于Stolz定理的证明.（2）和（3）由定义容易证明.
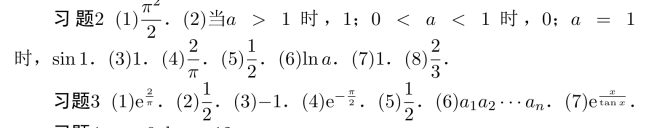
习题4 a=9，b=−12.
习题5 a=1，b=−4.
习题6 从略.
习题7 利用Stolz定理得到证明.
习题8 （1）数列{xn}单调下降且有界，得证极限为零；（2）利用习题7的结果证明.
习题9 e.
习题10 x=0为第二类间断点.
习题11 证明设
习题12 （1）数列的有界性，由
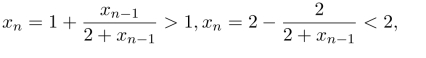
因此数列有界.
（2）由于
E.8 第七课答案
习题7.1 由于
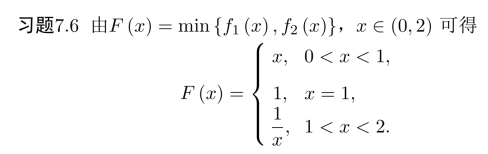
可以较容易地讨论F′（x）.
习题7.7 （1）连续性显然，
（B）正确；（C），（D）均不正确，反例为f（x）=sinx.
（2）（C）正确.
（3）（D）为选项.
习题7.12 （1）（B）正确；（A）只能得到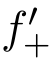
（0）存在；（C）为主干成立的必要而非充分条件；（D）不正确.
（2）（C）正确.
（3）（D）正确.
习题7.13 把绝对值根据x的定义域去掉，得到分段函数表达式，可得x=0，x=1处不可导，x=−1处可导.
习题7.14 由左右导数的定义可得函数的可导性，（D）为正确选项.
E.9 第八课答案
习题8.6 （1）注意到复合函数求导的链式法则，
E.10 第九课答案
E.11 第十课答案
习题10.1 ∀x∈（0，1），在（0，x），（x，1）分别利用Lagrange中值定理，存在ξ1∈（0，x），使得
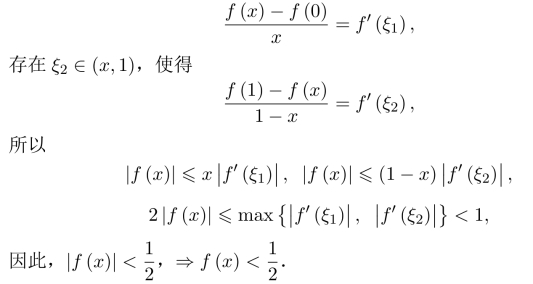
习题10.2 设g（x）=xf（x），利用Rolle定理得到证明.
习题10.3 利用g（x）=f（a+cx）−f（a−cx），利用Lagrange中值定理可得到证明.
习题10.4 存在ξ1∈（a，c），使得
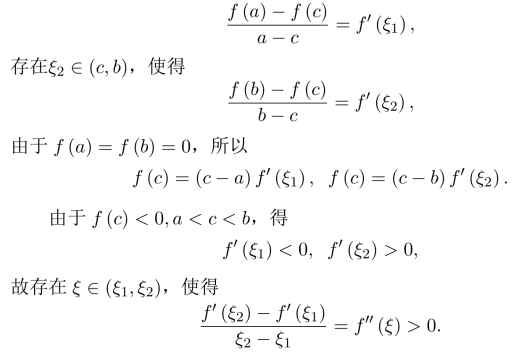
习题10.5 由于存在η∈（a，b），使得
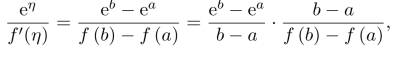
再利用Lagrange中值定理，存在ξ∈（a，b），使得
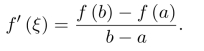
习题10.6 任意的正数是令F（x）=f（x）[f（1−x）]k，则
F(0)=F(1)=0,x∈(0,1)
存在ξ∈（0，1），使得
F′(ξ)=f′(ξ)[f(1−ξ)]k−kf(ξ)[f(1−ξ)]k−1f′(1−ξ)=0,
由f（x）＞0，两边同除以[f（1−ξ）]k−1，得到
习题10.7 第一步利用反证法，由Rolle定理导出矛盾；
第二步令G（x）=f（x）g′（x）−f′（x）g（x），利用Rolle定理得到证明.
习题10.8 令F（x）=f（x）·eg（x），利用中值定理可得到证明.
习题10.9 （1）令F（x）=f（x）+x−1，利用零点定理，可以得到.
（2）在[0，ξ]，[ξ，1]（ξ为（1）中的ξ）上分别利用Lagrange中值定理，存在η1∈（0，ξ），η2∈（ξ，1），使得
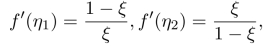
所以f′（η1）·f′（η2）=1.
习题10.10 设P∈（0，1），在（0，P），（P，1）上利用Lagrange中值定理，
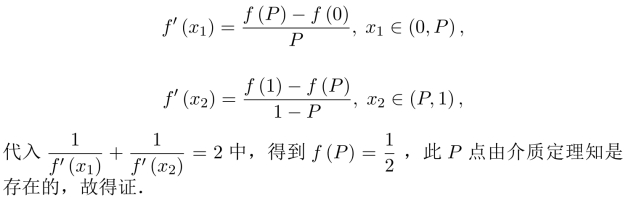
习题10.11 取z＞0且z＞a，则f（x）在区间[a，z]上存在最大值M，最小值m，如果M=m，则f（x）在区间[a，z]上为常数，则∀x∈[a，z]，f′（x）=0.
如果M≠m，设M＞m，则M，m中必有一个不为f（a），不妨设m＜f（a）.
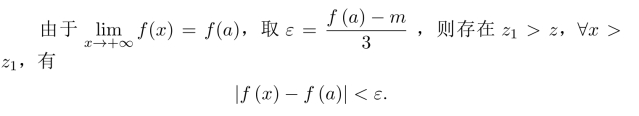
由ε的取值，当x＞z1时，f（x）＞m，因此f（x）在区间[a，+∞）上的最小值m′于（a，z1]上达到，又x＞z1时f（x）＞m，因此f（x）在区间（a，z1+1）内有最小值m，由Fermat定理，得f′（ξ）=0，ξ∈（a，z1+1）.
习题10.12 同习题10.10，当f（P）=
时满足要求，即可证明结论.
习题10.13 略.
习题10.14 略.
习题10.15 令h（x）=f（x）−g（x），
若f（x），g（x）于同一点x0∈（a，b）达到最大值，则h（x0）=0；
若f（x），g（x）分别于x1，x2达到最大值，则(https://www.daowen.com)
利用连续函数的零点存在定理，知在x1和x2间存在x0，使得f（x0）=0.再连续两次使用中值定理，得证.
习题10.16 利用函数极限的性质，存在x1∈（a，b）使得f（x1）＞0，再分别在[a，x1]及[x1，b]上利用Lagrange中值定理，可得证明.
E.12 第十一课答案
注 本题亦可利用L’Hospital法则来做，但是稍复杂一些.
习题11.4 （1）设f（x）=lnx，在[1，x]上利用Lagrange中值定理，存在ξ∈（1，x），使得
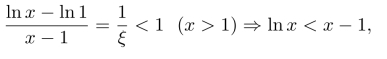
即ex＞ex.
（2）设f（x）=lnx，则当x＞0时，在[x，x+1]上利用Lagrange中值定理，存在ξ∈（x，x+1），使得
习题11.9 构造函数，利用函数的导数的性质得到证明.
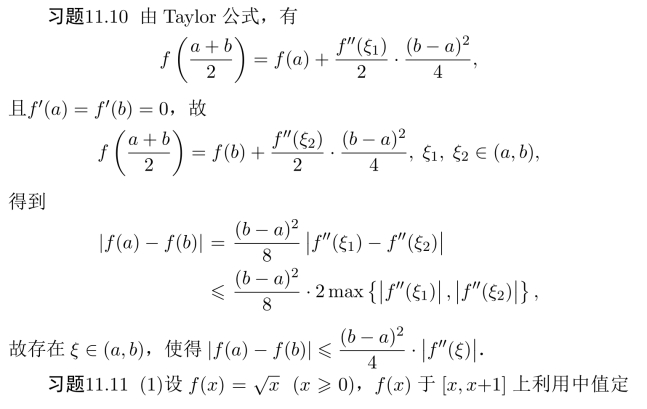
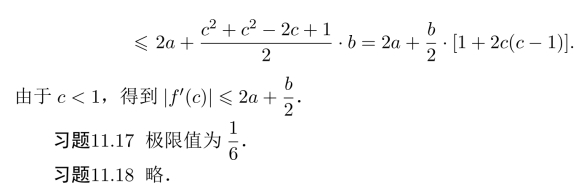
E.13 第十二课答案
得到
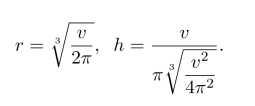
习题12.6 略.
习题12.7 考虑0＜x＜1，x＞1，x=1三种情况，将不等式化简，利用其导数的性质或者利用中值定理得到证明.
习题12.8
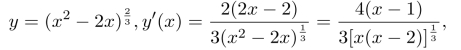
当x∈（0，1）时，y′（x）＞0，y（x）单调增加；
当x∈（1，2）时，y′（x）＜0，y（x）单调减少；
当x∈（2，3）时，y′（x）＞0，y（x）单调增加，故由y（0）=0，y（1）=1，y（2）=0，y（3）
习题12.9 （1）由于
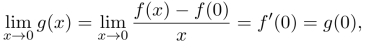
故g（x）于x=0点连续.
（2）由定义，得
当x＜0时，同理可以得到证明.
可据此确认凸区间、凹区间、拐点及极值，x轴为水平渐近线等.
习题12.11 由于f′（0）=f′′（0）=f′′′（0）=0，f（4）（0）=1＞0，A为答案.
习题12.12 函数y=e−x2sinx2为一偶函数，令t=x2，则求
的极值即可，由
E.14 第十三课答案
垂直渐近线x=−1，斜渐近线为y=x−1.
当x∈R时，f′（x）＜0，故f′（x）单调减少，又f（0）=1，f（x）＜0，当x＞1时，故存在唯一实根.
当n=2k时，
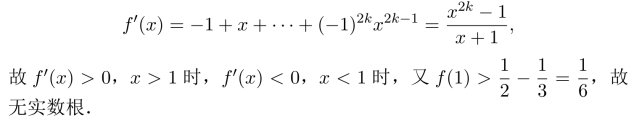
习题13.5 单增区间为（−∞，−1）和（0，+∞），单减区间为（−1，0）.
函数图形的渐近线为y=eπ（x−2）和y=x−2.
E.15 综合训练二答案
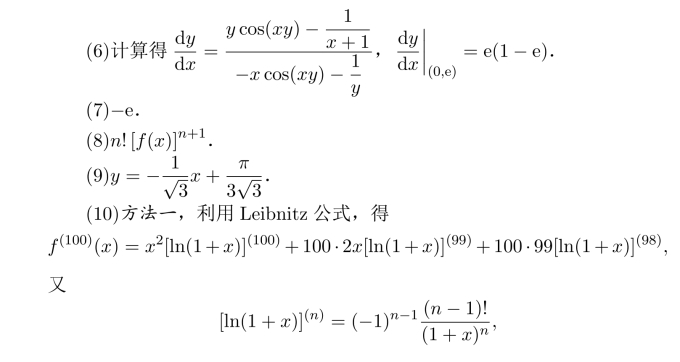
所以f（100）（0）=−9900·97！.
方法二，利用Taylor公式，将ln（1+x）在x=0点做Taylor展开，亦可得到.
（11）二阶导数值为−3.
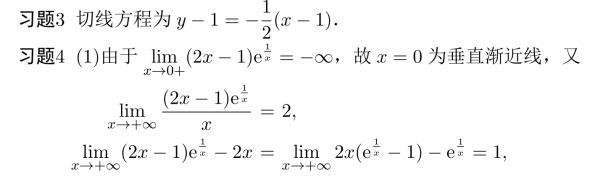
所以水平渐近线为y=2x+1.
（2）y=
，x=ξ，ξ满足2cosξ−5ξ=0.
习题5 因为f′（x）＞0，则f（x）严格单调增加，f′′（x）＞0，则f（x）是上凹的，又∆x＞0，故0＜dy＜∆y.选择答案为（A）.
习题6 从略.
习题7 从略.
习题8 （1）令F（x）=e−xf（x），在[a，b]上利用Rolle定理得到.
（2）由f′（a）f′（b）＞0，不妨设二者均大于0，则
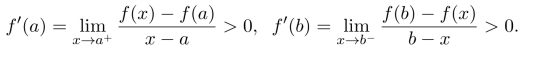
由函数的极限的性质，存在x1，x2∈（a，b）且x1＜x2，使得
故由零点存在定理，存在ξ∈（a，b），使得f（ξ）=0.
令F（x）=exf（x），在[a，ξ]和[ξ，b]上利用Lagrange中值定理，知存在ξ1∈（a，ξ），ξ2∈（ξ，b），满足
再令G（x）=e−x（f（x）+f′（x）），在[ξ1，ξ2]上利用Lagrange中值定理，可以得到证明.
注 由f′（a）f′（b）＞0，知存在ξ∈（a，b），使得f（ξ）=0，若f（a）=f（b）=0，则存在ξ1∈（a，ξ），ξ2∈（ξ，b），使得f′（ξ1）=f′（ξ2）=0，这一结果很重要，请读者注意.
习题9 利用三次中值定理.
习题10 令F（x）=ex（f（x）−1），利用Rolle定理可得到命题的证明.
习题11 Taylor公式ex=1+x+x2/2+x3/6+o（x3）代入已知等式得
[
习题13 通过条件及无穷小比较，可得到f（x）=2x2+o（x2），所以
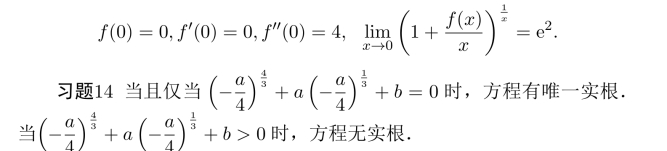
习题15 参考第七课中右导数和导函数的右极限证明.
习题16 利用Taylor展开，极限值为1/4.
习题17 （1）极限值为3e/2，（2）e1/3，（3）−1/2，（4）e−1/2，（5）
习题18 a=−1，b=−1/2，k=−1/3.
E.16 第十四课答案
习题14.1 （1）由分部积分，得
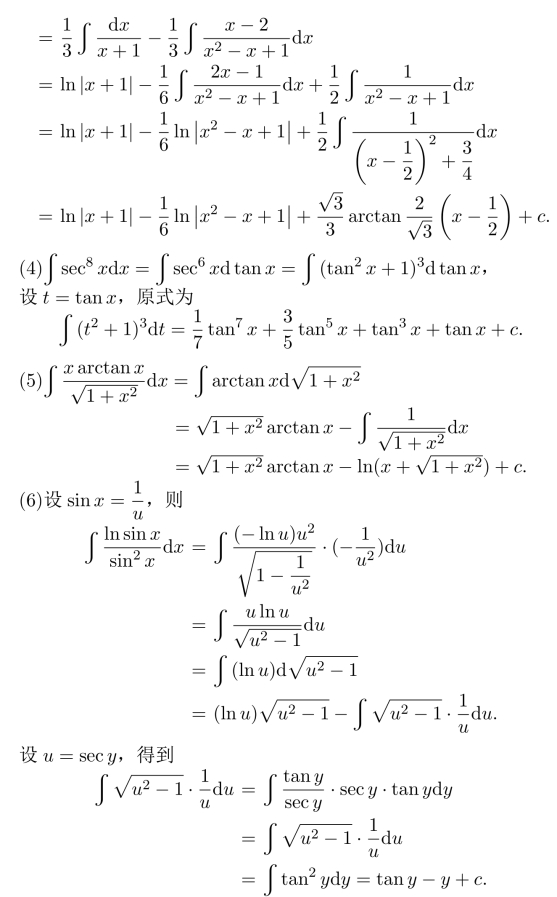
代回原变量即可.或者，原式为
习题14.3 由原函数的连续性，（D）为正确选项.
习题14.4 由于
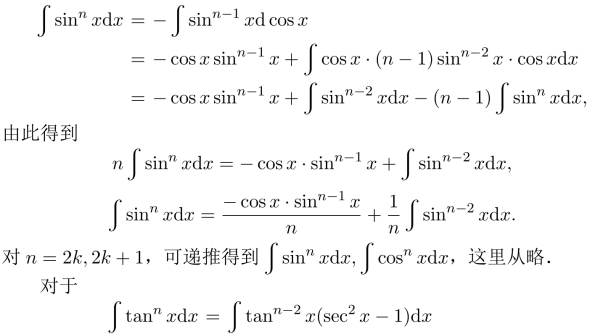
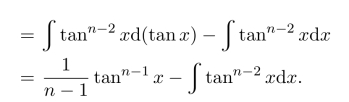
亦可考虑n为奇数、偶数时，递推计算，可得结果.这里从略.
E.17 第十五课答案
（4）答案略.
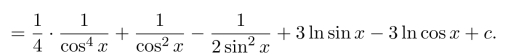
（5），（6），（7），（8）答案从略.
E.18 综合训练三答案
再换回变量.
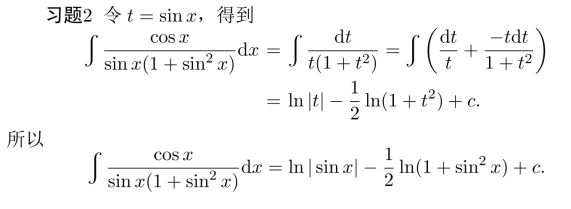
E.19 第十六课答案
故于[ξ，1]上，G（x）=xf（x）连续，在（ξ，1）内可导，由微分中值定理得：存在y∈（ξ，1），使得
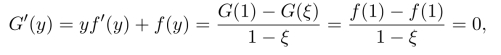
故存在y∈（ξ，1）⊂（0，1），得到ηf′（η）+f（η）=0.
习题16.7 利用积分中值定理及Lagrange中值定理可证得.
习题16.8 由Schwarz不等式，有
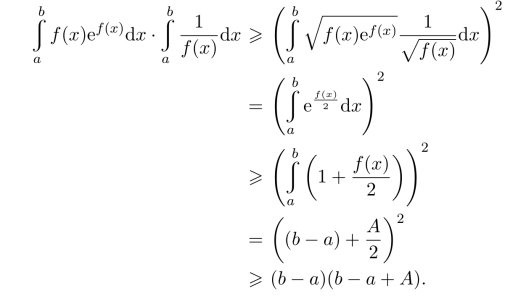
注 本练习也可以利用二重积分的知识求解.记
习题16.10 用导数定义证明.
习题16.11 由积分中值定理，存在η∈（0，2/π），使得ef（η）arctanη=π/4，令F（x）=ef（x）arctanx，则由微分中值定理，存在ξ∈（η，1），使得F′（ξ）=0，得证.
E.20 第十七课答案
习题17.1 （1）原式为
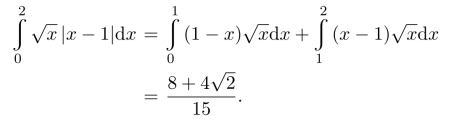
（2）利用偶函数的积分性质，有
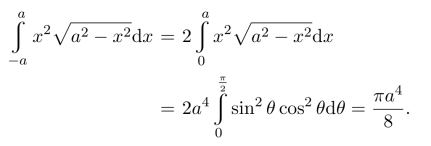
（3）利用分部积分，得
习题17.15 计算函数的一阶导数和二阶导数，可得单增区间（−1，0）∪（1，+∞），单减区间为（−∞，−1）∪（0，1），极小值f（−1）=f（1）=0，极大值f（0）=1/2−1/（2e）.
E.21 第十八课答案
E.22 综合训练四答案
（2）被积函数分子分母同乘以1+cosx，得
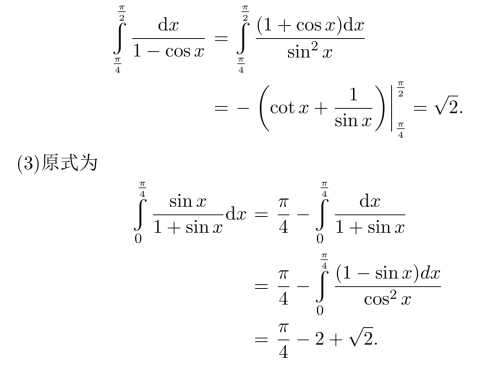
（4）定积分值为1.
习题6 a=16，b=7.
所以曲线L（在t＞0处）是上凸的.
（2）点为（2，3），切线方程为y=x+1.
（3）设L的方程x=g（y），则
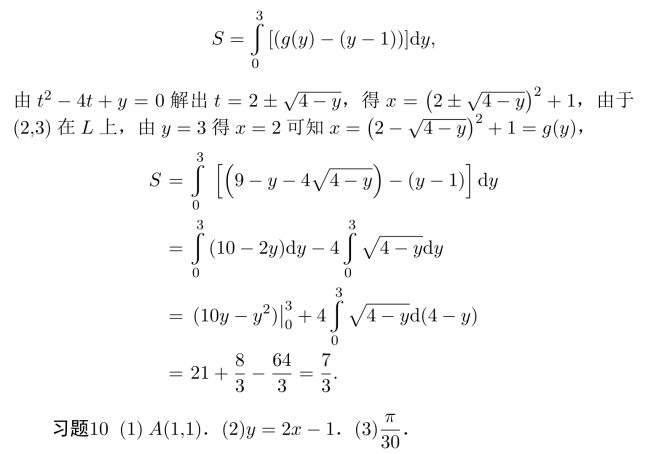
习题11 （1）利用反证法，假设当x∈[0，1]，恒有|f（x）|≤4成立，于
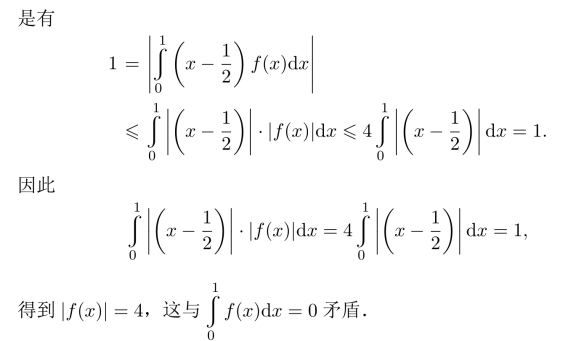
（2）仍然使用反证法，只需要证明存在x1∈[0，1]，使得|f（x1）|＜4即可.如若不然，则必有f（x）≥4或者f（x）≤−4成立，这与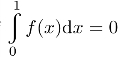
矛盾.再由连续性及（1）的结果，利用介值定理，可以得到（2）的证明.
习题12 f′（x）=4x2−2x，最小值f（1/2）=1/4.
E.23 综合训练五答案
习题7 旋转体的体积为π（e−1）.
习题8 利用变上限定积分的导数的运算，得到α=O（x），β=O（x3），γ=O（x2）.
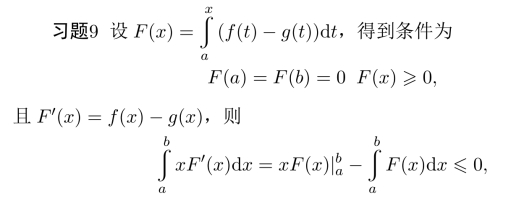
命题得证.
习题10 a=−1，b=0.
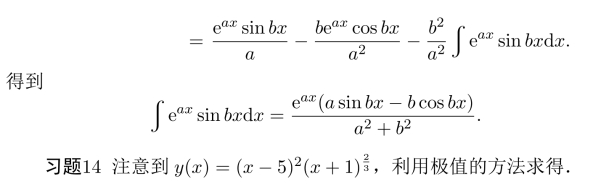
习题15 利用三角不等式和Cauchy判别法则可得到证明.
习题16 切线方程为y=x+1.
习题17 参考教科书证明.
习题19 由f′（a）f′（b）＞0，不妨设二者均大于0，根据导数的定义，存在x1，x2∈（a，b）且x1＜x2，使得f（x1）＞0，f（x2）＜0，故由零点存在定理，存在ξ∈（a，b），使得f（ξ）=0.再利用Rolle定理.
习题20 从略.
习题21 f（a），f（b）均在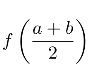
做Taylor展开，再相减，可得结果.
习题22 （1）a=−1；（2）a=−2.
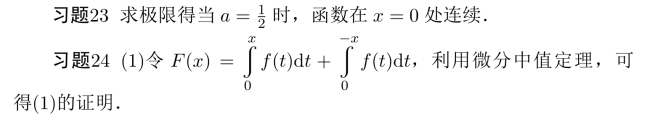
（2）由
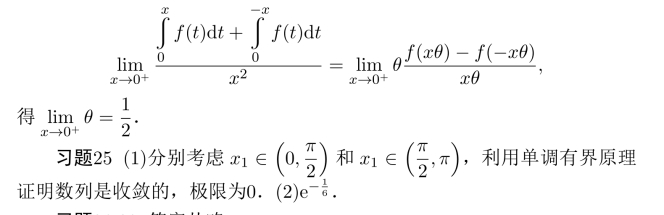
习题26 -28答案从略.
习题29 （1）由g（x）的有界性可得；
