18.1 本课重点内容提示
2026年01月14日
18.1 本课重点内容提示
1.定积分的几何应用.
(1)平面图形的面积、立体的体积
在直角坐标下由曲线y=f(x),y=g(x),f(x)≥g(x)及x=a,x=b所围平面图形的面积为
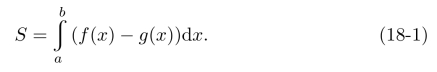
极坐标下由曲线r=r(θ)和射线θ=α,θ=β(α<β)所围曲边扇形的面积公式

曲线y=f(x)绕x轴旋转一周所得旋转体的体积为

(2)平面曲线的弧长、旋转曲面的面积
在直角坐标系下设曲线y=f(x)在[a,b]上具有连续导数,则其弧长
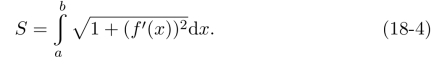 (https://www.daowen.com)
(https://www.daowen.com)
设曲线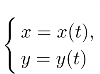 在α≤t≤β上具有连续切线(即x′(t),y′(t)连续),则其弧长
在α≤t≤β上具有连续切线(即x′(t),y′(t)连续),则其弧长
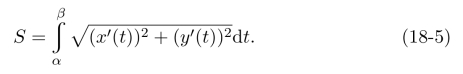
设极坐标曲线ρ=ρ(θ)在α≤θ≤β上具有连续切线(即ρ′(θ)连续),则其弧长
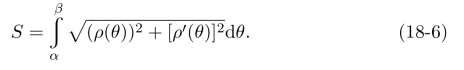
(3)旋转曲面的面积
设f′(x)在[a,b]上连续,则曲线段y=f(x),(a≤x≤b)绕x轴旋转所得旋转曲面的面积为
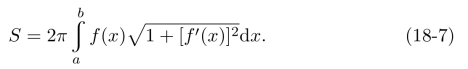
2.定积分在物理上的应用.
包括物体的重心、变力做功问题以及转动惯量的计算.
3.定积分在电学上的应用.
