18.3　课外练习

18.3　课外练习

A组

习题18.1　抛物线y2=2x将圆x2+y2=8分成两部分，试求这两部分的面积.

习题18.2　求抛物线y=−x2+4x−3及其在点（0，−3）和（3，0）处的切线所围图形的面积.

习题18.3　由心形线ρ=4（1+cosθ）和直线θ=0及θ=所围图形绕极轴旋转而成的旋转体的体积.

习题18.4　由星形线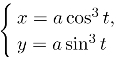（0≤t≤2π）绕x轴旋转而成的旋转体的体积.

习题18.5　求下面平面曲线的长度.

（1）求对数螺线ρ=keαθ在θ=α到θ=β（α＜β）之间的弧长；

（2）计算曲线y=ln（1−x2）上相应于的一段弧的长度.

B组

习题18.6　求由曲线y=−x3+x2+2x与x轴所围成的平面图形的面积.

习题18.7　设曲线y=ax2（a＞0，x≥0）与y=1−x2交于点A，过坐标原点O和A点的直线与曲线y=ax2围成一个平面图形，试问：

（1）当a为何值时，该图形绕x轴一周所得的旋转体体积最大？

（2）最大体积为多少？

习题18.8　设D是由曲线与x=cos3t，y=sin3t，（0≤t≤π/2）围成的平面区域，求D绕x轴旋转一周所得旋转体体积与表面积.