远期汇率是否是一个好的预测指标
下面我分析的另一个令人困惑的问题是远期汇率无法作为未来即期汇率的有效预测指标。首先我们来分析外汇市场的两个程式化事实，这两个事实可以很容易得到实证研究的支持，包括我的同事Mark Taylor和我做过的一些检验（Goodhart和Taylor，1987年）。第一，从1973年汇率开始自由浮动以来，在多数研究中，主要工业化国家的名义即期汇率非常接近于随机游走模式。[6]第二，在外汇市场上，有抵补利率平价（CIP）理论成立。[7]我们综合分析这两个程式化事实。如果从历史上看一个序列是随机游走变量，则其预期未来值应与其当前值相同。但如果有抵补利率平价理论成立，则远期汇率会偏离其当前即期汇率，偏离程度等于利差，因此远期汇率不是未来即期汇率的一个有效预测指标。
为了确定远期汇率是否是未来即期汇率的无偏和有效预测指标，标准的检验方法是对下式进行回归：
St+k-St=a+b（fkt-St）+Ut
其中，St是即期汇率的对数值，fkt是第k月远期汇率的对数值，Ut是误差项（见Fama，1984年；Boothe和Longworth，1986年）。如果fkt是St+k的无偏和有效预测指标，则我们可以预期a=0和b=1。在实践中，对该方程式的大量检验实际上都表明b值显著小于1，而且经常是负值。
下面将我的研究也加入到这些越来越多的文献中。我使用了表3所描述的9个数据集，这些数据集涉及不同时期和不同的双边汇率，而且样本包括了不同的时间频率。表4中列出了对上述方程式的回归结果。与预期相同，回归结果几乎都证实了早期的研究。在9个检验中，6个检验的b值是负数。尽管标准差相对较高，但9种情况中有5种情况b值系数显著（大于两个标准差）小于1。在任何情况下，都不能拒绝零假说，即b=0。
表3 数据集
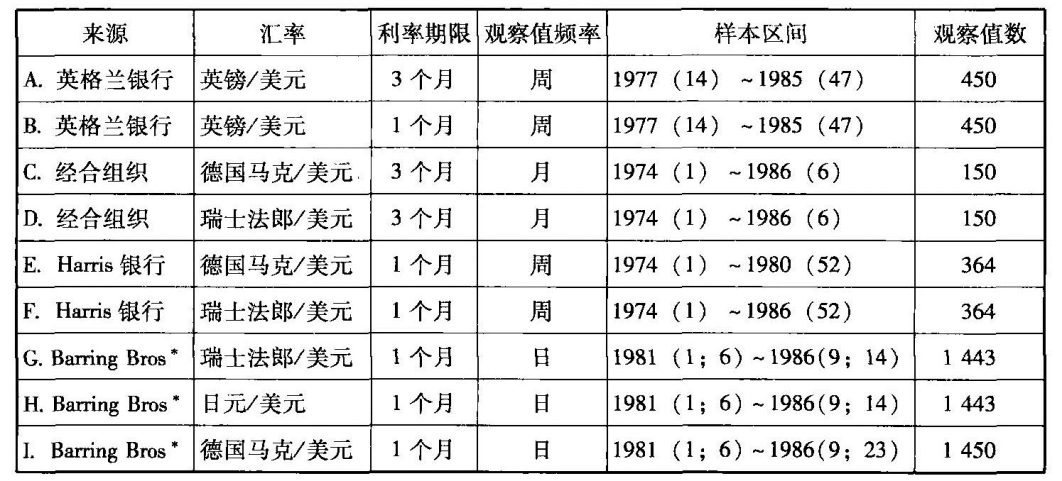
注：*在本数据集中，采集即期汇率的观察值和两种欧洲存款利率数据是在每天接近开盘的相同时间，根据抵补利率平价套利条件计算出当日远期汇率的估计值。
表4 结果
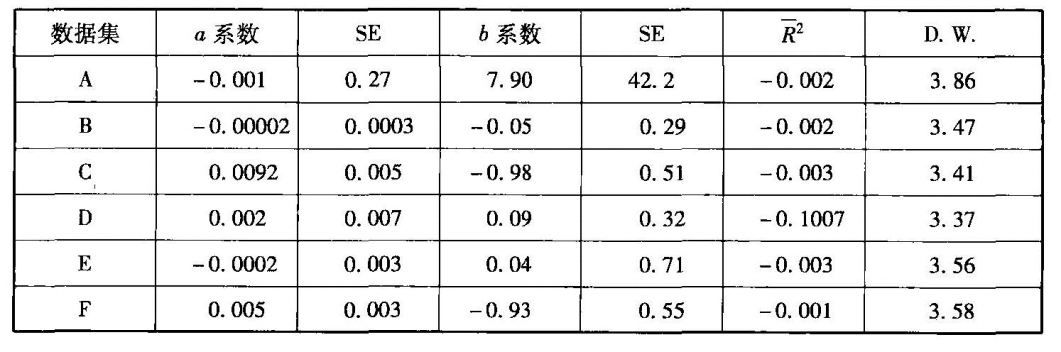
续表
方程式：即期t+n-即期t=a+b（远期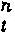
-即期t）（所有变量均为对数形式）。假设a=0；b=1。注：在所有数据集中，都有高于工具变量期限的较高频率观察值，即有重叠观察值（overlapping obersations）。根据Hansen（1982年）开发的技术，可以通过适当调整OLS协方差矩阵来解决该方法存在的计量经济问题，在所有检验中都进行了这种调整。
这些结果使我们处于一种困境，因为远期汇率本身似乎不仅不能提供关于即期汇率未来可能变化路径（
值单边无穷大）的有用信息，而且与远期汇率所包含的信息相比，似乎当前即期汇率水平包含了更多信息。
在远期汇率中真的发现不了有关未来汇率的信息吗？显然，就其本身而言，远期汇率实际上没有信息价值。但可能的情况是，当通过更有力的检验进行分析时，远期汇率和利差的滞后值具有某种预测即期汇率变化的（较弱）能力。伯明翰大学的Patrick McMahon和笔者分析了三变量的自回归问题。我们使用远期汇率、利差数据和以前即期汇率，目的是分析向量自回归是否和在多大程度上可以改善有关即期汇率的随机游走模型，或简单的单一变量回归模型。
以上进行了比较详细的分析，下面我想提出如下观点来结束本节内容：如果通过投机活动（这些投机活动是基于即期汇率随机游走的历史特征），远期汇率总是等于或非常接近于即期汇率，根据抵补利率平价理论，名义利差不能显著大于零。这意味着官方名义利率的升高会导致大规模资本流动和汇率的相应大幅度升值，以致由此造成的经济后果会促使国内利率立即回到与国外利率相符合的水平。显然，这种情况并没有出现。原因是对这类投机和相应的资本流动规模存在一定限制（换一种说法，远期汇率的相对被动性或松弛性使其不能成为无偏的预测指标），因此各国货币当局仍有自主性，而不会造成汇率的过度波动。